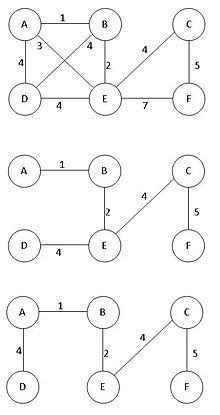
Minimum spanning tree

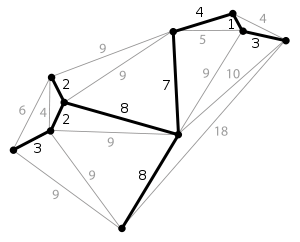The minimum spanning tree of a planar graph. Each edge is labeled with its weight, which here is roughly proportional to its length.

Given a connected, undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together. A single graph can have many different spanning trees. We can also assign a weight to each edge, which is a number representing how unfavorable it is, and use this to assign a weight to a spanning tree by computing the sum of the weights of the edges in that spanning tree. A minimum spanning tree (MST) or minimum weight spanning tree is then a spanning tree with weight less than or equal to the weight of every other spanning tree. More generally, any undirected graph (not necessarily connected) has a minimum spanning forest, which is a union of minimum spanning trees for its connected components.

One example would be a cable TV company laying cable to a new neighborhood. If it is constrained to bury the cable only along certain paths, then there would be a graph representing which points are connected by those paths. Some of those paths might be more expensive, because they are longer, or require the cable to be buried deeper; these paths would be represented by edges with larger weights. A spanning tree for that graph would be a subset of those paths that has no cycles but still connects to every house. There might be several spanning trees possible. A minimum spanning tree would be one with the lowest total cost.

Properties

Possible multiplicity

This figure shows there may be more than one minimum spanning tree in a graph. In the figure, the two trees below the graph are two possibilities of minimum spanning tree of the given graph.

There may be several minimum spanning trees of the same weight having a minimum number of edges; in particular, if all the edge weights of a given graph are the same, then every spanning tree of that graph is minimum. If there are n vertices in the graph, then each tree has n-1 edges.

Uniqueness

If each edge has a distinct weight then there will only be one, unique minimum spanning tree. This can be proved by induction or contradiction. This is true in many realistic situations, such as the cable TV company example above, where it's unlikely any two paths have exactly the same cost. This generalizes to spanning forests as well.

A proof of uniqueness by contradiction is as follows.^[1]

1. Say we have an algorithm that finds an MST (which we will call A) based on the structure of the graph and the order of the edges when ordered by weight. (Such algorithms do exist, see below.)
2. Assume MST A is not unique.
3. There is another spanning tree with equal weight, say MST B.
4. Let e1 be an edge that is in A but not in B.
5. As B is a MST, {e1} $\cup$ B must contain a cycle C.
6. Then B should include at least one edge e2 that is not in A and lies on C.
7. Assume the weight of e1 is less than that of e2.
8. Replace e2 with e1 in B yields the spanning tree {e1} $\cup$ B - {e2} which has a smaller weight compared to B.
9. Contradiction. As we assumed B is a MST but it is not.

If the weight of e1 is larger than that of e2, a similar argument involving tree {e2} $\cup$ A - {e1} also leads to a contradiction. Thus, we conclude that the assumption that there can be a second MST was false.

Minimum-cost subgraph

If the weights are positive, then a minimum spanning tree is in fact the minimum-cost subgraph connecting all vertices, since subgraphs containing cycles necessarily have more total weight.

Cycle property

For any cycle C in the graph, if the weight of an edge e of C is larger than the weights of other edges of C, then this edge cannot belong to an MST. Assuming the contrary, i.e. that e belongs to an MST T1, then deleting e will break T1 into two subtrees with the two ends of e in different subtrees. The remainder of C reconnects the subtrees, hence there is an edge f of C with ends in different subtrees, i.e., it reconnects the subtrees into a tree T2 with weight less than that of T1, because the weight of f is less than the weight of e.

Cut property

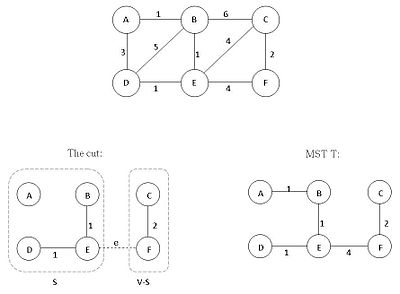This figure shows the cut property of MSP.T is the MST of the given graph. If S = {A,B,D,E}, thus V-S = {C,F},then there are 3 possibilities of the edge across the cut(S,V-S), they are edges BC, EC, EF of the original graph. Then, e is one of the minimum-weight-edge for the cut, therefore S ∪ {e} is part of the MST T.

For any cut C in the graph, if the weight of an edge e of C is smaller than the weights of all other edges of C, then this edge belongs to all MSTs of the graph. Indeed, assume the contrary, for example, edge BC (weighted 6) belongs to the MST T instead of edge e (weighted 4) in the left figure. Then adding e to T will produce a cycle, while replacing BC with e would produce MST of smaller weight.

Minimum-cost edge

If the edge of a graph with the minimum cost e is unique, then this edge is included in any MST. Indeed, if e was not included in the MST, removing any of the (larger cost) edges in the cycle formed after adding e to the MST, would yield a spanning tree of smaller weight.

Algorithms

The first algorithm for finding a minimum spanning tree was developed by Czech scientist Otakar Borůvka in 1926 (see Borůvka's algorithm). Its purpose was an efficient electrical coverage of Moravia. There are now two algorithms commonly used, Prim's algorithm and Kruskal's algorithm. All three are greedy algorithms that run in polynomial time, so the problem of finding such trees is in FP, and related decision problems such as determining whether a particular edge is in the MST or determining if the minimum total weight exceeds a certain value are in P. Another greedy algorithm not as commonly used is the reverse-delete algorithm, which is the reverse of Kruskal's algorithm.

If the edge weights are integers, then deterministic algorithms are known that solve the problem in O(m + n) integer operations.^[2] In a comparison model, in which the only allowed operations on edge weights are pairwise comparisons, Karger, Klein & Tarjan (1995) found a linear time randomized algorithm based on a combination of Borůvka's algorithm and the reverse-delete algorithm.^[3][4] Whether the problem can be solved deterministically in linear time by a comparison-based algorithm remains an open question, however. The fastest non-randomized comparison-based algorithm, by Bernard Chazelle, is based on the soft heap, an approximate priority queue.^[5][6] Its running time is O(m α(m,n)), where m is the number of edges, n is the number of vertices and α is the classical functional inverse of the Ackermann function. The function α grows extremely slowly, so that for all practical purposes it may be considered a constant no greater than 4; thus Chazelle's algorithm takes very close to linear time. Seth Pettie and Vijaya Ramachandran have found a provably optimal deterministic comparison-based minimum spanning tree algorithm, the computational complexity of which is unknown.^[7]

Research has also considered parallel algorithms for the minimum spanning tree problem. With a linear number of processors it is possible to solve the problem in O(log n) time.^[8][9] Bader & Cong (2003) demonstrate an algorithm that can compute MSTs 5 times faster on 8 processors than an optimized sequential algorithm.^[10] Typically, parallel algorithms are based on Borůvka algorithm—Prim's and especially Kruskal's algorithm do not scale as well to additional processors.

Other specialized algorithms have been designed for computing minimum spanning trees of a graph so large that most of it must be stored on disk at all times. These external storage algorithms, for example as described in "Engineering an External Memory Minimum Spanning Tree Algorithm" by Roman Dementiev et al.,^[11] can operate, by authors' claims, as little as 2 to 5 times slower than a traditional in-memory algorithm. They rely on efficient external storage sorting algorithms and on graph contraction techniques for reducing the graph's size efficiently.

The problem can also be approached in a distributed manner. If each node is considered a computer and no node knows anything except its own connected links, one can still calculate the distributed minimum spanning tree.

MST on complete graphs

Alan M. Frieze showed that given a complete graph on n vertices, with edge weights that are independent identically distributed random variables with distribution function F satisfying F'(0) > 0, then as n approaches +∞ the expected weight of the MST approaches ζ(3) / F'(0), where ζ is the Riemann zeta function. Under the additional assumption of finite variance, Alan M. Frieze also proved convergence in probability. Subsequently, J. Michael Steele showed that the variance assumption could be dropped.

In later work, Svante Janson proved a central limit theorem for weight of the MST.

For uniform random weights in [0,1], the exact expected size of the minimum spanning tree has been computed for small complete graphs.^[12]

Vertices	Expected size	Approximative expected size
2	1 / 2	0.5
3	3 / 4	0.75
4	31 / 35	0.8857143
5	893 / 924	0.9664502
6	278 / 273	1.0183151
7	30739 / 29172	1.053716
8	199462271 / 184848378	1.0790588
9	126510063932 / 115228853025	1.0979027

Related problems

A related problem is the k-minimum spanning tree (k-MST), which is the tree that spans some subset of k vertices in the graph with minimum weight.

A set of k-smallest spanning trees is a subset of k spanning trees (out of all possible spanning trees) such that no spanning tree outside the subset has smaller weight.^[13][14][15] (Note that this problem is unrelated to the k-minimum spanning tree.)

The Euclidean minimum spanning tree is a spanning tree of a graph with edge weights corresponding to the Euclidean distance between vertices which are points in the plane (or space).

The rectilinear minimum spanning tree is a spanning tree of a graph with edge weights corresponding to the rectilinear distance between vertices which are points in the plane (or space).

In the distributed model, where each node is considered a computer and no node knows anything except its own connected links, one can consider distributed minimum spanning tree. Mathematical definition of the problem is the same but has different approaches for solution.

The capacitated minimum spanning tree is a tree that has a marked node (origin, or root) and each of the subtrees attached to the node contains no more than a c nodes. c is called a tree capacity. Solving CMST optimally requires exponential time, but good heuristics such as Esau-Williams and Sharma produce solutions close to optimal in polynomial time.

The degree constrained minimun spanning tree is a minimun spanning tree in with each vertex is connected to no more than d other vertices, for some given number d. The case d = 2 is a special case of the traveling salesman problem, so the degree constrained minimum spanning tree is NP-hard in general.

For directed graphs, the minimum spanning tree problem is called the Arborescence problem and can be solved in quadratic time using the Chu–Liu/Edmonds algorithm.

A maximum spanning tree is a spanning tree with weight greater than or equal to the weight of every other spanning tree. Such a tree can be found with algorithms such as Prim's or Kruskal's after multiplying the edge weights by -1 and solving the MST problem on the new graph. A path in the maximum spanning tree is the widest path in the graph between its two endpoints: among all possible paths, it maximizes the weight of the minimum-weight edge.^[16]

The dynamic MST problem concerns the update of a previously computed MST after an edge weight change in the original graph or the insertion/deletion of a vertex.^[17][18]

Minimum bottleneck spanning tree

A bottleneck edge is the highest weighted edge in a spanning tree.

A spanning tree is a minimum bottleneck spanning tree (or MBST) if the graph does not contain a spanning tree with a smaller bottleneck edge weight.

A MST is necessarily a MBST (provable by the cut property), but a MBST is not necessarily a MST. If the bottleneck edge in a MBST is a bridge in the graph, then all spanning trees are MBSTs.

See also

• Reverse-Delete algorithm
• Dijkstra's algorithm
• Spanning tree protocol, used in switched networks
• Minimum spanning tree-based image segmentation
• Edmonds's algorithm
• Distributed minimum spanning tree
• Prim's algorithm
• Kruskal's algorithm
• Steiner tree
• Borůvka's algorithm

References

1. ^ Gallager, R. G.; Humblet, P. A.; Spira, P. M. (January 1983), "A distributed algorithm for minimum-weight spanning trees", ACM Transactions on Programming Languages and Systems 5 (1): 66–77, doi:10.1145/357195.357200 .
2. ^ Fredman, M. L.; Willard, D. E. (1994), "Trans-dichotomous algorithms for minimum spanning trees and shortest paths", Journal of Computer and System Sciences 48 (3): 533–551, doi:10.1016/S0022-0000(05)80064-9, MR1279413 .
3. ^ Karger, David R.; Klein, Philip N.; Tarjan, Robert E. (1995), "A randomized linear-time algorithm to find minimum spanning trees", Journal of the Association for Computing Machinery 42 (2): 321–328, doi:10.1145/201019.201022, MR1409738 
4. ^ Pettie, Seth; Ramachandran, Vijaya (2002), "Minimizing randomness in minimum spanning tree, parallel connectivity, and set maxima algorithms", Proc. 13th ACM-SIAM Symposium on Discrete Algorithms (SODA '02), San Francisco, California, pp. 713–722, http://portal.acm.org/citation.cfm?id=545477 .
5. ^ Chazelle, Bernard (2000), "A minimum spanning tree algorithm with inverse-Ackermann type complexity", Journal of the Association for Computing Machinery 47 (6): 1028–1047, doi:10.1145/355541.355562, MR1866456 .
6. ^ Chazelle, Bernard (2000), "The soft heap: an approximate priority queue with optimal error rate", Journal of the Association for Computing Machinery 47 (6): 1012–1027, doi:10.1145/355541.355554, MR1866455 .
7. ^ Pettie, Seth; Ramachandran, Vijaya (2002), "An optimal minimum spanning tree algorithm", Journal of the Association for Computing Machinery 49 (1): 16–34, doi:10.1145/505241.505243, MR2148431 .
8. ^ Chong, Ka Wong; Han, Yijie; Lam, Tak Wah (2001), "Concurrent threads and optimal parallel minimum spanning trees algorithm", Journal of the Association for Computing Machinery 48 (2): 297–323, doi:10.1145/375827.375847, MR1868718 .
9. ^ Pettie, Seth; Ramachandran, Vijaya (2002), "A randomized time-work optimal parallel algorithm for finding a minimum spanning forest", SIAM Journal on Computing 31 (6): 1879–1895, doi:10.1137/S0097539700371065, MR1954882 .
10. ^ Bader, David A.; Cong, Guojing (2006), "Fast shared-memory algorithms for computing the minimum spanning forest of sparse graphs", Journal of Parallel and Distributed Computing 66 (11): 1366–1378, doi:10.1016/j.jpdc.2006.06.001 .
11. ^ Dementiev, Roman; Sanders, Peter; Schultes, Dominik; Sibeyn, Jop F. (2004), "Engineering an external memory minimum spanning tree algorithm", Proc. IFIP 18th World Computer Congress, TC1 3rd International Conference on Theoretical Computer Science (TCS2004), pp. 195–208, http://algo2.iti.kit.edu/dementiev/files/emst.pdf .
12. ^ Steele, J. Michael (2002), "Minimal spanning trees for graphs with random edge lengths", Mathematics and computer science, II (Versailles, 2002), Trends Math., Basel: Birkhäuser, pp. 223–245, MR1940139 
13. ^ Gabow, Harold N. (1977), "Two algorithms for generating weighted spanning trees in order", SIAM Journal on Computing 6 (1): 139–150, MR0441784 .
14. ^ Eppstein, David (1992), "Finding the k smallest spanning trees", BIT 32 (2): 237–248, doi:10.1007/BF01994879, MR1172188 .
15. ^ Frederickson, Greg N. (1997), "Ambivalent data structures for dynamic 2-edge-connectivity and k smallest spanning trees", SIAM Journal on Computing 26 (2): 484–538, doi:10.1137/S0097539792226825, MR1438526 .
16. ^ Hu, T. C. (1961), "The maximum capacity route problem", Operations Research 9 (6): 898–900, JSTOR 167055 .
17. ^ Spira, P. M.; Pan, A. (1975), "On finding and updating spanning trees and shortest paths", SIAM Journal on Computing 4 (3): 375–380, MR0378466 .
18. ^ Holm, Jacob; de Lichtenberg, Kristian; Thorup, Mikkel (2001), "Poly-logarithmic deterministic fully dynamic algorithms for connectivity, minimum spanning tree, 2-edge, and biconnectivity", Journal of the Association for Computing Machinery 48 (4): 723–760, doi:10.1145/502090.502095, MR2144928 .

Additional reading

• Graham, R. L.; Hell, Pavol (1985), "On the history of the minimum spanning tree problem", Annals of the History of Computing 7 (1): 43–57, doi:10.1109/MAHC.1985.10011, MR783327 .
• Otakar Boruvka on Minimum Spanning Tree Problem (translation of the both 1926 papers, comments, history) (2000) Jaroslav Nesetril, Eva Milková, Helena Nesetrilová. (Section 7 gives his algorithm, which looks like a cross between Prim's and Kruskal's.)
• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Chapter 23: Minimum Spanning Trees, pp. 561–579.
• Eisner, Jason (1997). State-of-the-art algorithms for minimum spanning trees: A tutorial discussion. Manuscript, University of Pennsylvania, April. 78 pp.
• Kromkowski, John David. "Still Unmelted after All These Years", in Annual Editions, Race and Ethnic Relations, 17/e (2009 McGraw Hill) (Using minimum spanning tree as method of demographic analysis of ethnic diversity across the United States).

External links

• Jeff Erickson's MST lecture notes
• Implemented in BGL, the Boost Graph Library
• The Stony Brook Algorithm Repository - Minimum Spanning Tree codes
• Implemented in QuickGraph for .Net