Hubble's law

Physical cosmology
Universe · Big Bang Age of the universe Timeline of the Big Bang Ultimate fate of the universe
Early universe Inflation · Nucleosynthesis GWB · Neutrino background Cosmic microwave background
Expanding universe Redshift · Hubble's law Metric expansion of space Friedmann equations FLRW metric
Structure formation Shape of the universe Structure formation Reionization Galaxy formation Large-scale structure Galaxy filament
Components Lambda-CDM model Dark energy · Dark matter Dark fluid · Dark flow
Timeline Timeline of cosmological theories Future of an expanding universe
Experiments Observational cosmology 2dF · SDSS COBE · BOOMERanG · WMAP · Planck
Scientists Isaac Newton · Einstein · Hawking · Friedman · Lemaître · Hubble · Penzias · Wilson · Gamow · Dicke · Zel'dovich · Mather · Rubin · Smoot · others
v · d · e

Hubble's law is the name for the astronomical observation in physical cosmology first made by American astronomer Edwin Hubble, that: (1) all objects observed in deep space (interstellar space) are found to have a doppler shift observable relative velocity to Earth, and to each other; and (2) that this doppler-shift-measured velocity, of various galaxies receding from the Earth, is proportional to their distance from the Earth and all other interstellar bodies. In effect, the space-time volume of the observable universe is expanding and Hubble's law is the direct physical observation of this process.^[1] The law was first derived from the General Relativity equations by Georges Lemaître in 1927.^[2] Edwin Hubble derived it empirically in 1929^[3] after nearly a decade of observations. The recession velocity of the objects was inferred from their redshifts, many measured earlier by Vesto Slipher (1917) and related to velocity by him.^[4] It is considered the first observational basis for the expanding space paradigm and today serves as one of the pieces of evidence most often cited in support of the Big Bang model.

The law is often expressed by the equation v = H₀D, with H₀ the constant of proportionality (the Hubble constant) between the "proper distance" D to a galaxy (which can change over time, unlike the comoving distance) and its velocity v (i.e. the derivative of proper distance with respect to cosmological time coordinate; see Uses of the proper distance for some discussion of the subtleties of this definition of 'velocity'). The SI unit of H₀ is s⁻¹ but it is most frequently quoted in (km/s)/Mpc, thus giving the speed in km/s of a galaxy 1 megaparsec (3.09×10¹⁹ km) away. The reciprocal of H₀ is the Hubble time.

A recent 2011 estimate of the Hubble constant, which used a new infrared camera on the Hubble Space Telescope (HST) to measure the distance and redshift for a collection of astronomical objects, gives a value of H₀ = 73.8 ± 2.4 (km/s)/Mpc.^[5][6] An alternate approach using data from galactic clusters gave a value of H₀ = 67.0 ± 3.2 (km/s)/Mpc.^[7][8]

An observational determination of the Hubble constant obtained in 2010 based on measurements of gravitational lensing by using the HST yielded a value of H₀ = 72.6 ± 3.1 (km/s)/Mpc.^[9] WMAP seven-year results, also from 2010, gave an estimate of H₀ = 71.0 ± 2.5 (km/s)/Mpc based on WMAP data alone, and an estimate of H₀ = 70.4 +1.3
−1.4 (km/s)/Mpc based on WMAP data with Gaussian priors based on earlier estimates from other studies.^[10] In 2009 also using the Hubble Space Telescope the measure was 74.2 ± 3.6 (km/s)/Mpc.^[11] The results agree closely with an earlier measurement, based on observations by the HST of Cepheid variable stars, of H₀ = 72 ± 8 km/s/Mpc obtained in 2001.^[12] In August 2006, a less-precise figure was obtained independently using data from NASA's Chandra X-ray Observatory: H₀ = 77 (km/s)/Mpc or about 2.5×10⁻¹⁸ s⁻¹ with an uncertainty of ± 15%.^[13] NASA's WMAP site summarizes existing data to indicate a constant of 70.8 ± 1.6 (km/s)/Mpc if space is assumed to be flat, or 70.8 ± 4.0 (km/s)/Mpc otherwise,^[14] although these estimates have been on the site since January 2007^[15] and may not take into account the more recent studies discussed above.

Discovery

A decade before Hubble made his observations, a number of physicists and mathematicians had established a consistent theory of the relationship between space and time by using Einstein's field equations of general relativity. Applying the most general principles to the nature of the universe yielded a dynamic solution that conflicted with the then prevailing notion of a static universe.

FLRW equations

In 1922, Alexander Friedmann derived his Friedmann equations from Einstein's field equations, showing that the universe might expand at a rate calculable by the equations.^[16] The parameter used by Friedmann is known today as the scale factor which can be considered as a scale invariant form of the proportionality constant of Hubble's law. Georges Lemaître independently found a similar solution in 1927. The Friedmann equations are derived by inserting the metric for a homogeneous and isotropic universe into Einstein's field equations for a fluid with a given density and pressure. This idea of an expanding spacetime would eventually lead to the Big Bang and Steady State theories of cosmology.

Shape of the universe

Before the advent of modern cosmology, there was considerable talk about the size and shape of the universe. In 1920, the famous Shapley-Curtis debate took place between Harlow Shapley and Heber D. Curtis over this issue. Shapley argued for a small universe the size of the Milky Way galaxy and Curtis argued that the universe was much larger. The issue was resolved in the coming decade with Hubble's improved observations.

Cepheid variable stars outside of the Milky Way

Edwin Hubble.

Edwin Hubble did most of his professional astronomical observing work at Mount Wilson Observatory, the world's most powerful telescope at the time. His observations of Cepheid variable stars in spiral nebulae enabled him to calculate the distances to these objects. Surprisingly, these objects were discovered to be at distances which placed them well outside the Milky Way. They continued to be called "nebulae" and it was only gradually that the term "galaxies" took over.

Combining redshifts with distance measurements

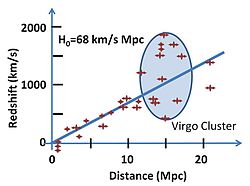
Fit of redshift velocities to Hubble's law; patterned after William C. Keel (2007). The Road to Galaxy Formation. Berlin: Springer published in association with Praxis Pub., Chichester, UK. ISBN 3540725342. http://books.google.com/?id=BUgJGypUYF0C&pg=PA8. Various estimates for the Hubble constant exist. The HST Key H₀ Group fitted type Ia supernovae for redshifts between 0.01 and 0.1 to find that H₀ = 71 ± 2(statistical) ± 6 (systematic) km s⁻¹Mpc⁻¹,^[17] while Sandage et al. find H₀ = 62.3 ± 1.3 (statistical) ± 5 (systematic) km s⁻¹Mpc⁻¹.^[18]

The parameters that appear in Hubble’s law: velocities and distances, are not directly measured. In reality we determine, say, a supernova brightness, which provides information about its distance, and the redshift z = ∆λ/λ of its spectrum of radiation. Hubble correlated brightness and parameter z.

Combining his measurements of galaxy distances with Vesto Slipher and Milton Humason's measurements of the redshifts associated with the galaxies, Hubble discovered a rough proportionality between redshift of an object and its distance. Though there was considerable scatter (now known to be caused by peculiar velocities - the 'Hubble flow' is used to refer to the region of space far enough out that the recession velocity is larger than local peculiar velocities), Hubble was able to plot a trend line from the 46 galaxies he studied and obtain a value for the Hubble constant of 500 km/s/Mpc (much higher than the currently accepted value due to errors in his distance calibrations). (See cosmic distance ladder for details.)

At the time of discovery and development of Hubble’s law it was acceptable to explain redshift phenomenon as a Doppler shift in the context of special relativity, and use the Doppler formula to associate redshift z with velocity. Today the velocity-distance relationship of Hubble's law is viewed as a theoretical result with velocity to be connected with observed redshift not by the Doppler effect, but by a cosmological model relating recessional velocity to the expansion of the universe. Even for small z the velocity entering the Hubble law is no longer interpreted as a Doppler effect, although at small z the velocity-redshift relation for both interpretations is the same.

In 1958, the first good estimate of H₀, 75 km/s/Mpc, was published by Allan Sandage,^[19] but it would be decades before a consensus was achieved.

Hubble Diagram

Hubble's law can be easily depicted in a "Hubble Diagram" in which the velocity (assumed approximately proportional to the redshift) of an object is plotted with respect to its distance from the observer.^[20] A straight line of positive slope on this diagram is the visual depiction of Hubble's law.

The cosmological constant abandoned

Main article: Cosmological constant

After Hubble's discovery was published, Albert Einstein abandoned his work on the cosmological constant, which he had designed to modify his equations of general relativity, to allow them to produce a static solution which, as originally formulated, his equations did not admit.^{[citation needed]} He later termed this work his "greatest blunder" since it was his incorrect presumption of a static universe that had caused him to fail to accept what could be seen in his concepts and equations of general relativity:^{[citation needed]} the fact that general relativity was both predicting and providing the means for calculating the expansion of the universe, which (like the bending of light by large masses or the precession of the orbit of Mercury) could be experimentally observed and compared to his theoretical calculations using particular solutions of the equations of general relativity as he had originally formulated them.

Einstein made a famous trip to Mount Wilson in 1931 to thank Hubble for providing the observational basis for modern cosmology.^{[citation needed]}

The cosmological constant has regained attention in recent decades as a hypothesis for dark energy.^{[citation needed]}

Interpretation

A variety of possible recessional velocity vs. redshift functions including the simple linear relation v = cz; a variety of possible shapes from theories related to general relativity; and a curve that does not permit speeds faster than light in accordance with special relativity. All curves are linear at low redshifts. See Davis and Lineweaver.^[21]

The discovery of the linear relationship between redshift and distance, coupled with a supposed linear relation between recessional velocity and redshift, yields a straightforward mathematical expression for Hubble's Law as follows:

$v = H_0 \, D$

where

• v is the recessional velocity, typically expressed in km/s.
• H₀ is Hubble's constant and corresponds to the value of H (often termed the Hubble parameter which is a value that is time dependent and which can be expressed in terms of the scale factor) in the Friedmann equations taken at the time of observation denoted by the subscript 0. This value is the same throughout the universe for a given comoving time.
• D is the proper distance (which can change over time, unlike the comoving distance which is constant) from the galaxy to the observer, measured in mega parsecs (Mpc), in the 3-space defined by given cosmological time. (Recession velocity is just v = dD/dt).

Hubble's law is considered a fundamental relation between recessional velocity and distance. However, the relation between recessional velocity and redshift depends on the cosmological model adopted, and is not established except for small redshifts.

For distances D larger than the radius of the Hubble sphere r_HS , objects recede at a rate faster than the speed of light (See Uses of the proper distance for a discussion of the significance of this):

$r_{HS} = \frac{c}{H_0} \ .$

Since the Hubble "constant" is only a constant in space, not in time, the radius of the Hubble sphere may increase or decrease over various time intervals. The subscript '0' indicates the value of the Hubble constant today.^[22] Current evidence suggests the expansion of the universe is accelerating (see Accelerating universe), meaning that for any given galaxy, the recession velocity dD/dt is increasing over time as the galaxy moves to greater and greater distances; however, the Hubble parameter is actually thought to be decreasing with time, meaning that if we were to look at some fixed distance D and watch a series of different galaxies pass that distance, later galaxies would pass that distance at a smaller velocity than earlier ones.^[23]

Redshift velocity and recessional velocity

Redshift can be measured by determining the wavelength of a known transition, such as hydrogen α-lines for distant quasars, and finding the fractional shift compared to a stationary reference. Thus redshift is a quantity unambiguous for experimental observation. The relation of redshift to recessional velocity is another matter. For an extensive discussion, see Harrison.^[24]

Redshift velocity

The redshift z often is described as a redshift velocity, which is the recessional velocity that would produce the same redshift if it were caused by a linear Doppler effect (which, however, is not the case, as the shift is caused in part by a cosmological expansion of space, and because the velocities involved are too large to use a non-relativistic formula for Doppler shift). This redshift velocity can easily exceed the speed of light.^[25] In other words, to determine the redshift velocity v_rs, the relation:

$v_{rs} \equiv cz \ ,$

is used.^[26][27] That is, there is no fundamental difference between redshift velocity and redshift: they are rigidly proportional, and not related by any theoretical reasoning. The motivation behind the "redshift velocity" terminology is that the redshift velocity agrees with the velocity from a low-velocity simplification of the so-called Fizeau-Doppler formula^[28]

$z = \frac{\lambda_o}{\lambda_e}-1 = \sqrt{\frac{1+v/c}{1-v/c}}-1 \approx \frac{v}{c} \ .$

Here, λ_o, λ_e are the observed and emitted wavelengths respectively. The "redshift velocity" v_rs is not so simply related to real velocity at larger velocities, however, and this terminology leads to confusion if interpreted as a real velocity. Next, the connection between redshift or redshift velocity and recessional velocity is discussed. This discussion is based on Sartori.^[29]

Recessional velocity

Suppose R(t) is called the scale factor of the universe, and increases as the universe expands in a manner that depends upon the cosmological model selected. Its meaning is that all measured distances D(t) between co-moving points increase proportionally to R. (The co-moving points are not moving relative to each other except as a result of the expansion of space.) In other words:

$\frac {D(t)}{D(t_0)} = \frac {R(t)}{R(t_0)} \ ,$

where t₀ is some reference time. If light is emitted from a galaxy at time t_e and received by us at t₀, it is red shifted due to the expansion of space, and this redshift z is simply:

$z = \frac {R(t_0)}{R(t_e)} - 1 \ .$

Suppose a galaxy is at distance D, and this distance changes with time at a rate d_tD . We call this rate of recession the "recession velocity" v_r:

$v_r = d_tD = \frac {d_tR}{R} D \ .$

We now define the Hubble constant as

$H \equiv \frac {d_tR}{R} \ ,$

and discover the Hubble law:

$v_r = H D \ .$

From this perspective, Hubble's law is a fundamental relation between (i) the recessional velocity contributed by the expansion of space and (ii) the distance to an object; the connection between redshift and distance is a crutch used to connect Hubble's law with observations. This law can be related to redshift z approximately by making a Taylor series expansion:

$z = \frac {R(t_0)}{R(t_e)} - 1 \approx \frac {R(t_0)} {R(t_0)\left(1+(t_e-t_0)H(t_0)\right)}-1 \approx (t_0-t_e)H(t_0) \ ,$

If the distance is not too large, all other complications of the model become small corrections and the time interval is simply the distance divided by the speed of light:

$z \approx (t_0-t_e)H(t_0) \approx \frac {D}{c} H(t_0) \ ,$ or $cz \approx D H(t_0) = v_r \ .$

According to this approach, the relation cz = v_r is an approximation valid at low redshifts, to be replaced by a relation at large redshifts that is model-dependent. See velocity-redshift figure.

Observability of parameters

Strictly speaking, neither v nor D in the formula are directly observable, because they are properties now of a galaxy, whereas our observations refer to the galaxy in the past, at the time that the light we currently see left it.

For relatively nearby galaxies (redshift z much less than unity), v and D will not have changed much, and v can be estimated using the formula v = zc where c is the speed of light. This gives the empirical relation found by Hubble.

For distant galaxies, v (or D) cannot be calculated from z without specifying a detailed model for how H changes with time. The redshift is not even directly related to the recession velocity at the time the light set out, but it does have a simple interpretation: (1+z) is the factor by which the universe has expanded while the photon was travelling towards the observer.

Expansion velocity vs relative velocity

In using Hubble's law to determine distances, only the velocity due to the expansion of the universe can be used. Since gravitationally interacting galaxies move relative to each other independent of the expansion of the universe, these relative velocities, called peculiar velocities, need to be accounted for in the application of Hubble's law.

The Finger of God effect, discovered in 1938 by Benjamin Kenneally, is one result of this phenomenon. In systems that are gravitationally bound, such as galaxies or our planetary system, the expansion of space is a much weaker effect than the attractive force of gravity.

Idealized Hubble's Law

The mathematical derivation of an idealized Hubble's Law for a uniformly expanding universe is a fairly elementary theorem of geometry in 3-dimensional Cartesian/Newtonian coordinate space, which, considered as a metric space, is entirely homogeneous and isotropic (properties do not vary with location or direction). Simply stated the theorem is this:

Any two points which are moving away from the origin, each along straight lines and with speed proportional to distance from the origin, will be moving away from each other with a speed proportional to their distance apart.

In fact this applies to non-Cartesian spaces as long as they are locally homogeneous and isotropic; specifically to the negatively- and positively-curved spaces frequently considered as cosmological models (see shape of the universe).

An observation stemming from this theorem is that seeing objects recede from us on Earth is not an indication that Earth is near to a center from which the expansion is occurring, but rather that every observer in an expanding universe will see objects receding from them.

The ‘ultimate fate’ and age of the universe

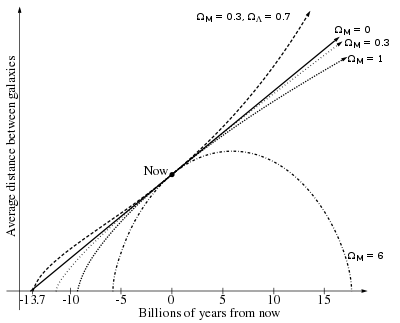The age and ultimate fate of the universe can be determined by measuring the Hubble constant today and extrapolating with the observed value of the deceleration parameter, uniquely characterized by values of density parameters (Ω_M for matter and Ω_Λ for dark energy). A "closed universe" with Ω_M > 1 and Ω_Λ = 0 comes to an end in a Big Crunch and is considerably younger than its Hubble age. An "open universe" with Ω_M ≤ 1 and Ω_Λ = 0 expands forever and has an age that is closer to its Hubble age. For the accelerating universe with nonzero Ω_Λ that we inhabit, the age of the universe is coincidentally very close to the Hubble age.

The value of the Hubble parameter changes over time either increasing or decreasing depending on the sign of the so-called deceleration parameter q which is defined by

$q = -\left(1+\frac{\dot H}{H^2}\right).$

In a universe with a deceleration parameter equal to zero, it follows that H = 1/t, where t is the time since the Big Bang. A non-zero, time-dependent value of q simply requires integration of the Friedmann equations backwards from the present time to the time when the comoving horizon size was zero.

It was long thought that q was positive, indicating that the expansion is slowing down due to gravitational attraction. This would imply an age of the universe less than 1/H (which is about 14 billion years). For instance, a value for q of 1/2 (once favoured by most theorists) would give the age of the universe as 2/(3H). The discovery in 1998 that q is apparently negative means that the universe could actually be older than 1/H. However, estimates of the age of the universe are very close to 1/H.

Olbers' paradox

Main article: Olbers' paradox

The expansion of space summarized by the Big Bang interpretation of Hubble's Law is relevant to the old conundrum known as Olbers' paradox: if the universe were infinite, static, and filled with a uniform distribution of stars, then every line of sight in the sky would end on a star, and the sky would be as bright as the surface of a star. However, the night sky is largely dark. Since the 17th century, astronomers and other thinkers have proposed many possible ways to resolve this paradox, but the currently accepted resolution depends in part upon the Big Bang theory and in part upon the Hubble expansion. In a universe that exists for a finite amount of time, only the light of finitely many stars has had a chance to reach us yet, and the paradox is resolved. Additionally, in an expanding universe distant objects recede from us, which causes the light emanating from them to be redshifted and diminished in brightness. Although both effects contribute, the redshift is the less important of the two.^[30]

Determining the Hubble constant

“

Astrophysicists are always wrong, but never in doubt. ... RP Kirshner[31]

”

The value of the Hubble constant is estimated by measuring the redshift of distant galaxies and then determining the distances to the same galaxies (by some other method than Hubble's law). Uncertainties in the physical assumptions used to determine these distances have caused varying estimates of the Hubble constant. For most of the second half of the 20th century the value of H₀ was estimated to be between 50 and 90 (km/s)/Mpc.

The value of the Hubble constant was the topic of a long and rather bitter controversy between Gérard de Vaucouleurs who claimed the value was around 100 and Allan Sandage who claimed the value was near 50.^[32] In 1996, a debate moderated by John Bahcall between Gustav Tammann and Sidney van den Bergh was held in similar fashion to the earlier Shapley-Curtis debate over these two competing values.

This wide variance in estimates was partially resolved with the introduction of the ΛCDM model of the universe in the late 1990s. With the ΛCDM model observations of high-redshift clusters at X-ray and microwave wavelengths using the Sunyaev-Zel'dovich effect, measurements of anisotropies in the cosmic microwave background radiation, and optical surveys all gave a value of around 70 for the constant.^{[citation needed]}

Using Hubble space telescope data

The Hubble Key Project (led by Dr. Wendy L. Freedman, Carnegie Observatories) used the Hubble space telescope to establish the most precise optical determination in May 2001^[33] of 72 ± 8 (km/s)/Mpc, consistent with a measurement of H₀ based upon Sunyaev-Zel'dovich effect observations of many galaxy clusters having a similar accuracy.

Using WMAP data

The most precise cosmic microwave background radiation determinations were 71 ± 4 (km/s)/Mpc, by WMAP in 2003, and 70.4 +1.5
−1.6 (km/s)/Mpc, for measurements up to 2006.^[34] The five year release from WMAP in 2008 found 71.9 +2.6
−2.7 (km/s)/Mpc using WMAP-only data and 70.1 ± 1.3 (km/s)/Mpc when data from other studies was incorporated,^[35] while the seven year release in 2010 found H₀ = 71.0 ± 2.5 (km/s)/Mpc using WMAP-only data and H₀ = 70.4 +1.3
−1.4 (km/s)/Mpc when data from other studies was incorporated.^[10]

These values arise from fitting a combination of WMAP and other cosmological data to the simplest version of the ΛCDM model. If the data is fitted with more general versions, H₀ tends to be smaller and more uncertain: typically around 67 ± 4 (km/s)/Mpc although some models allow values near 63 (km/s)/Mpc.^[36]

Using Chandra X-ray Observatory data

In August 2006, using NASA's Chandra X-ray Observatory, a team from NASA's Marshall Space Flight Center (MSFC) found the Hubble constant to be 77 (km/s)/Mpc, with an uncertainty of about 15%.^[37] The consistency of the measurements from all these methods lends support to both the measured value of H₀ and the ΛCDM model.

Acceleration of the expansion

Main article: Accelerating universe

A value for q measured from standard candle observations of Type Ia supernovae, which was determined in 1998 to be negative, surprised many astronomers with the implication that the expansion of the universe is currently "accelerating" (although the Hubble factor is still decreasing with time, as mentioned above in the Interpretation section; see the articles on dark energy and the ΛCDM model).

Derivation of the Hubble parameter

Start with the Friedmann equation:

$H^2 \equiv \left(\frac{\dot{a}}{a}\right)^2 = \frac{8 \pi G}{3}\rho - \frac{kc^2}{a^2}+ \frac{\Lambda}{3},$

where H is the Hubble parameter, a is the scale factor, G is the gravitational constant, k is the normalised spatial curvature of the universe and equal to −1, 0, or +1, and Λ is the cosmological constant.

Matter-dominated universe (with a cosmological constant)

If the universe is matter-dominated, then the mass density of the universe ρ can just be taken to include matter so

$\rho = \rho_m(a) = \frac{\rho_{m_{0}}}{a^3},$

where $\rho_{m_{0}}$ is the density of matter today. We know for nonrelativistic particles that their mass density decreases proportional to the inverse volume of the universe so the equation above must be true. We can also define (see density parameter for Ω_m)

$\rho_c = \frac{3 H^2}{8 \pi G};$

$\Omega_m \equiv \frac{\rho_{m_{0}}}{\rho_c} = \frac{8 \pi G}{3 H_0^2}\rho_{m_{0}};$

so ρ = ρ_cΩ_m / a³. Also, by definition,

$\Omega_k \equiv \frac{-kc^2}{(a_0H_0)^2}$

and

$\Omega_{\Lambda} \equiv \frac{\Lambda c^2}{3H_0^2},$

where the subscript nought refers to the values today, and a₀ = 1. Substituting all of this in into the Friedman equation at the start of this section and replacing a with a = 1 / (1 + z) gives

$H^2(z)= H_0^2 \left( \Omega_M (1+z)^{3} + \Omega_k (1+z)^{2} + \Omega_{\Lambda} \right).$

Matter- and dark energy-dominated universe

If the universe is both matter-dominated and dark energy- dominated, then the above equation for the Hubble parameter will also be a function of the equation of state of dark energy. So now:

ρ = ρ_m(a) + ρ_de(a),

where ρ_de is the mass density of the dark energy. By definition an equation of state in cosmology is P = wρc², and if we substitute this into the fluid equation, which describes how the mass density of the universe evolves with time,

$\dot{\rho}+3\frac{\dot{a}}{a}\left(\rho+\frac{P}{c^2}\right)=0;$

$\frac{d\rho}{\rho}=-3\frac{da}{a}\left(1+w\right).$

If w is constant,

$\ln{\rho}=-3\left(1+w\right)\ln{a};$

$\rho=a^{-3\left(1+w\right)}.$

Therefore for dark energy with a constant equation of state w, $\rho_{de}(a)= \rho_{de0}a^{-3\left(1+w\right)}$. If we substitute this into the Friedman equation in a similar way as before, but this time set k = 0 which is assuming we live in a spatially flat universe, (see Shape of the Universe)

$H^2(z)= H_0^2 \left( \Omega_M (1+z)^{3} + \Omega_{de}(1+z)^{3\left(1+w \right)} \right).$

If dark energy does not have a constant equation-of-state w, then

$\rho_{de}(a)= \rho_{de0}e^{-3\int\frac{da}{a}\left(1+w(a)\right)},$

and to solve this we must parametrize w(a), for example if w(a) = w₀ + w_a(1 − a), giving

$H^2(z)= H_0^2 \left( \Omega_M a^{-3} + \Omega_{de}a^{-3\left(1+w_0 +w_a \right)}e^{-3w_a(1-a)} \right).$

Units derived from the Hubble constant

Hubble time

The Hubble constant H₀ has units of inverse time, i.e. H₀ ~ 2.3×10⁻¹⁸ s⁻¹. “Hubble time” is defined as 1 / H₀. The value of Hubble time in the standard cosmological model is 4.35×10¹⁷ s or 13.8 billion years. (Liddle 2003, p. 57) The phrase "expansion timescale" means "Hubble time".[1] If the value of H₀ were to stay constant, a naive interpretation of the Hubble time is that it is the time taken for the universe to increase in size by a factor of e (because the solution of dx/dt = xH₀ is x = s₀exp(H₀t), where s₀ is the size of some feature at some arbitrary initial condition t = 0). However, over long periods of time the dynamics are complicated by general relativity, dark energy, inflation, etc., as explained above.

Hubble length

The Hubble length or Hubble distance is a unit of distance in cosmology, defined as c / H₀—the speed of light multiplied by the Hubble time. It is equivalent to 4228 million parsecs or 13.8 billion light years. (The numerical value of the Hubble length in light years is, by definition, equal to that of the Hubble time in years.) The Hubble distance would be the distance at which galaxies are currently receding from us at the speed of light, as can be seen by substituting D = c/H₀ into the equation for Hubble's law, v = H₀D.

Hubble volume

The Hubble volume is sometimes defined as a volume of the universe with a comoving size of c / H₀. The exact definition varies: it is sometimes defined as the volume of a sphere with radius c / H₀, or alternatively, a cube of side c / H₀. Some cosmologists even use the term Hubble volume to refer to the volume of the observable universe, although this has a radius approximately three times larger.

See also

• Age of the universe
• Shape of the universe

Notes

1. ^ Peter Coles, ed (2001). Routledge Critical Dictionary of the New Cosmology. Routledge. p. 202. ISBN 0203164571. http://books.google.com/?id=BgNGWVr5yhIC&pg=PA202. 
2. ^ Lemaître, Georges (1927). "Un univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques". Annales de la Société Scientifique de Bruxelles A47: 49–56. Bibcode 1927ASSB...47...49L  (Full article, PDF). Partially translated (the translator remains unidentified) in Lemaître, Georges (1931). "Expansion of the universe, A homogeneous universe of constant mass and increasing radius accounting for the radial velocity of extra-galactic nebulæ". Monthly Notices of the Royal Astronomical Society 91: 483–490. Bibcode 1931MNRAS..91..483L .
3. ^ Hubble, Edwin, "A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae" (1929) Proceedings of the National Academy of Sciences of the United States of America, Volume 15, March 15, 1929: Issue 3, pp. 168-173, communicated January 17, 1929 (Full article, PDF)
4. ^ Malcolm S Longair (2006). The Cosmic Century. Cambridge University Press. p. 109. ISBN 0521474361. http://books.google.com/?id=z0vlYHQZHJcC&pg=RA2-PA109. 
5. ^ Riess, Adam G.; Lucas Macri, Stefano Casertano, Hubert Lampeitl, Henry C. Ferguson, Alexei V. Filippenko, Saurabh W. Jha, Weidong Li, Ryan Chornock (1 April 2011). "A 3% Solution: Determination of the Hubble Constant With the Hubble Space Telescope and Wide Field Camera". The Astrophysics Journal 730 (2): 119. Bibcode 2011ApJ...730..119R. doi:10.1088/0004-637X/730/2/119. http://hubblesite.org/pubinfo/pdf/2011/08/pdf.pdf. 
6. ^ 'New Study Gives Dark Energy A Boost' (Ron Cowen), Science News, 16 March 2011.
7. ^ Beutler, Florian; Chris Blake, Matthew Colless, D. Heath Jones, Lister Staveley-Smith, Lachlan Campbell, Quentin Parker, Will Saunders, Fred Watson (25 July 2011). "The 6dF Galaxy Survey: Baryon Acoustic Oscillations and the Local Hubble Constant". Monthly Notices of the Royal Astronomical Society 416 (4): 3017. Bibcode 2011MNRAS.tmp.1164B. doi:10.1111/j.1365-2966.2011.19250.x. 
8. ^ 'Hubble Constant: A New Way to Measure the Expansion of the Universe', Science Daily, 27 July 2011.
9. ^ S. H. Suyu, P. J. Marshall, M. W. Auger, S. Hilbert, R. D. Blandford, L. V. E. Koopmans, C. D. Fassnacht and T. Treu. Dissecting the Gravitational Lens B1608+656. II. Precision Measurements of the Hubble Constant, Spatial Curvature, and the Dark Energy Equation of State. The Astrophysical Journal, 2010; 711 (1): 201 DOI: 10.1088/0004-637X/711/1/201
10. ^ ^{a b} "Seven-Year Wilson Microwave Anisotropy Probe (WMAP) Observations: Sky Maps, Systematic Errors, and Basic Results" (PDF). nasa.gov. http://lambda.gsfc.nasa.gov/product/map/dr4/pub_papers/sevenyear/basic_results/wmap_7yr_basic_results.pdf. Retrieved 2010-12-02.  (see p. 39 for a table of best estimates for various cosmological parameters)
11. ^ "Refined Hubble Constant Narrows Possible Explanations for Dark Energy". 2009-05-09. http://hubblesite.org/newscenter/archive/releases/2009/08/full/. Retrieved 2009-05-09. 
12. ^ W. L. Freedman, B. F. Madore, B. K. Gibson, L. Ferrarese, D. D. Kelson, S. Sakai, J. R. Mould, R. C. Kennicutt, Jr., H. C. Ford, J. A. Graham, J. P. Huchra, S. M. G. Hughes, G. D. Illingworth, L. M. Macri, P. B. Stetson (2001). "Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant". The Astrophysical Journal 553 (1): 47–72. arXiv:astro-ph/0012376. Bibcode 2001ApJ...553...47F. doi:10.1086/320638. 
13. ^ "Chandra Confirms the Hubble Constant". 2006-08-08. http://www.universetoday.com/2006/08/08/chandra-confirms-the-hubble-constant/. Retrieved 2007-03-07. 
14. ^ "WMAP's Universe". NASA. http://wmap.gsfc.nasa.gov/universe/uni_expansion.html. 
15. ^ archived version of page from 2007-01-01 (see last paragraph)
16. ^ Friedman, A. (1922). "Über die Krümmung des Raumes". Zeitschrift für Physik 10 (1): 377–386. Bibcode 1922ZPhy...10..377F. doi:10.1007/BF01332580 . (English translation: Friedman, A. (1999). "On the Curvature of Space". General Relativity and Gravitation 31 (12): 1991–2000. Bibcode 1999GReGr..31.1991F. doi:10.1023/A:1026751225741 .)
17. ^ Wendy L Freeman et al. (2001). "Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant". Astrophys J 553 (1): 47–72. arXiv:astro-ph/0012376. Bibcode 2001ApJ...553...47F. doi:10.1086/320638. 
18. ^ Steven Weinberg (2008). Cosmology. Oxford University Press. p. 28. ISBN 0198526822. http://books.google.com/?id=nqQZdg020fsC&pg=PA28. 
19. ^ Sandage, A. R. (May,1958). "Current Problems in the Extragalactic Distance Scale". Astrophysical Journal 127 (3): 513–526. Bibcode 1958ApJ...127..513S. doi:10.1086/146483. 
20. ^ R. P. Kirshner, Hubble's Diagram and Cosmic Expansion, Online Article
21. ^ Tamara M. Davis, Charles H. Lineweaver (2000). "Superluminal Recessional Velocities". arXiv:astro-ph/0011070 [astro-ph]. doi:10.1063/1.1363540. 
22. ^ William C. Keel (2007). The Road to Galaxy Formation (2 ed.). Springer. p. 7. ISBN 3540725342. http://books.google.com/?id=BUgJGypUYF0C&pg=PA7. 
23. ^ Is the universe expanding faster than the speed of light? (see final paragraph)
24. ^ Edward Harrison (1992). "The redshift-distance and velocity-distance laws". Astrophysical Journal, Part 1 403: 28–31. Bibcode 1993ApJ...403...28H. doi:10.1086/172179. . A pdf file can be found here.
25. ^ MS Madsen (1995). The Dynamic Cosmos. CRC Press. p. 35. ISBN 0412623005. http://books.google.com/?id=_2GeJxVvyFMC&pg=PA35. 
26. ^ Avishai Dekel, J. P. Ostriker (1999). Formation of Structure in the Universe. Cambridge University Press. p. 164. ISBN 0521586321. http://books.google.com/?id=yAroX6tx-l0C&pg=PA164. 
27. ^ Thanu Padmanabhan (1993). Structure formation in the universe. Cambridge University Press. p. 58. ISBN 0521424860. http://books.google.com/?id=AJlOVBRZJtIC&pg=PA58. 
28. ^ Leo Sartori (1996). Understanding Relativity. University of California Press. p. 163, Appendix 5B. ISBN 0520200292. 
29. ^ Leo Sartori (1996). [0520200292 Understanding Relativity]. University of California Press. pp. 304–305. ISBN 0520079868. 0520200292. 
30. ^ S. I. Chase, Olbers' Paradox, entry in the Physics FAQ; see also I. Asimov, "The Black of Night", in Asimov on Astronomy (Doubleday, 1974), ISBN 0-385-04111-X.
31. ^ Quoted by RP Kirshner
32. ^ Dennis Overbye, Lonely Hearts of the Cosmos: The Scientific Quest for the Secret of the Universe, Harper-Collins (1991), ISBN 0-06-015964-2 & ISBN 0-330-29585-3 (finalist, Nation Book Critics Circle Award for non-fiction). Second edition (with new afterword), Back Bay, 1999. Gives an account of the history of the dispute and rivalries.
33. ^ W. L. Freedman, B. F. Madore, B. K. Gibson, L. Ferrarese, D. D. Kelson, S. Sakai, J. R. Mould, R. C. Kennicutt, Jr., H. C. Ford, J. A. Graham, J. P. Huchra, S. M. G. Hughes, G. D. Illingworth, L. M. Macri, P. B. Stetson (2001). "Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant". The Astrophysical Journal 553 (1): 47–72. arXiv:astro-ph/0012376. Bibcode 2001ApJ...553...47F. doi:10.1086/320638. . Preprint available here.
34. ^ D. N. Spergel et al. (2007). "Three-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Implications for Cosmology". Astrophysical Journal Supplement Series 170 (2): 377–408. arXiv:astro-ph/0603449. Bibcode 2007ApJS..170..377S. doi:10.1086/513700. ; available online at LAMBDA
35. ^ Table 7 of Hinshaw, G. (WMAP Collaboration). et al. (feb 2009). "Five-Year Wilkinson Microwave Anisotropy Probe Observations: Data Processing, Sky Maps, and Basic Results". The Astrophysical Journal Supplement 180 (2): 225–245. arXiv:0803.0732. Bibcode 2009ApJS..180..225H. doi:10.1088/0067-0049/180/2/225.  (Table is on p. 54)
36. ^ Results for H₀ and other cosmological parameters obtained by fitting a variety of models to several combinations of WMAP and other data are available at the NASA's LAMBDA website.
37. ^ Chandra independently determines Hubble constant in Spaceflight Now

References

• Kutner, Marc (2003). Astronomy: A Physical Perspective. New York: Cambridge University Press. ISBN 0521529271 
• Hubble, E. P. (1937). The Observational Approach to Cosmology. Oxford: Clarendon Press 
• Eng, A. E. (1985). A New Approach to Starlight Runs. Oswego 
• Liddle, Andrew R. (2003). An Introduction to Modern Cosmology (2nd ed.). Chichester: Wiley. ISBN 0470848359 

External links

• The Hubble Key Project
• The Hubble Diagram Project