Neutron cross section

Science with Neutrons
Foundations
Neutron temperature Flux · Radiation · Transport Cross section · Absorption · Activation
Neutron scattering
Neutron diffraction Small-angle neutron scattering GISANS Reflectometry Inelastic neutron scattering Triple-axis spectrometer Time-of-flight spectrometer Backscattering spectrometer Spin-echo spectrometer
Other applications
Radiography and tomography Activation analysis · Prompt gamma activation analysis Fundamental research with neutrons: Ultracold neutrons · Interferometry
Infrastructure
Neutron sources: Research reactor · Spallation · Neutron moderator Neutron optics: Guide · Supermirror · Polarizer Detection
Neutron facilities
America: HFIR · LANSCE · NIST CNR -SNS Australia: OPAL Asia: J-PARC Europe: BER II · FRM II · ILL · ISIS · JINR · LLB · PINS · SINQ Historic: IPNS · HFBR Planned: ESS User Affiliations: ENSA
v · d · e

Physics portal

In nuclear and particle physics, the concept of a neutron cross section is used to express the likelihood of interaction between an incident neutron and a target nucleus. In conjunction with the neutron flux, it enables the calculation of the reaction rate, for example to derive the thermal power of a nuclear power plant. The standard unit for measuring the cross section is the barn, which is equal to 10^-28 m² or 10^-24 cm².

Parameters of interest

The neutron cross section, and therefore the probability of an interaction, depends on:

• the target type (hydrogen, uranium…),
• the type of nuclear reaction (scattering, fission…).
• the incident particle energy, also called speed or temperature (thermal, fast…),

and, to a lesser extent, of:

• its relative angle between the incident neutron and the target nuclide,
• the target nuclide temperature.

Target type dependence

The neutron cross section is defined for a given type of target particle. For example, the capture cross section of hydrogen-2 (referred to as deuterium) is much smaller than that of common hydrogen-1^[1] . This is the reason why some reactors use heavy water (in which most of the hydrogen is deuterium) instead of ordinary light water as moderator: fewer neutrons are lost by capture inside the medium, hence enabling the use of natural uranium instead of enriched uranium. This is the principle of a CANDU reactor.

Type of reaction dependence

The likelihood of interaction between an incident neutron and a target nuclide, independent of the type of reaction, is expressed with the help of the total cross section σ_T. However, it may be useful to know if the incoming particle bounces off the target (and therefore continue travelling after the interaction) or disappears after the reaction. For that reason, the scattering and absorption cross sections σ_S and σ_A are defined and the total cross section is simply the sum of the two partial cross sections ^[2]:

σ_T = σ_S + σ_A

Absorption cross section

If the neutron is absorbed when approaching the nuclide, the atomic nucleus moves up on the table of isotopes by one position. For instance, U-235 becomes U-236* with the * indicating the nucleus is highly energized. This energy has to be released and the release can take place through any of several mechanisms.

1. The simplest way for the release to occur is for the neutron to be ejected by the nucleus. If the neutron is emitted immediately, it acts the same as in other scattering events.
2. The nucleus may emit gamma radiation.
3. The nucleus may β^- decay, where a neutron is converted into a proton, an electron and an electron-type antineutrino (the antiparticle of the neutrino)
4. About 81% of the U-236* nuclei are so energized that they undergo fission, releasing the energy as kinetic motion of the fission fragments, also emitting between one and five free neutrons.

• Nuclei that undergo fission as their predominant decay method after neutron capture include U-233, U-235, U-237, Pu-239, Pu-241.
• Nuclei that predominantly absorb neutrons and then emit Beta particle radiation lead to these isotopes, e.g., Th-232 absorbs a neutron and becomes Th-233*, which emits a Beta particle and becomes Pa-233, which emits another Beta particle to become U-233.
• Isotopes that undergo Beta emission transmute from one element to another element, those that undergo gamma or X-ray emission don't change in element or isotope.

Scattering cross-section

The scattering cross-section can be further subdivided into coherent scattering and incoherent scattering, which is caused by the spin dependence of the scattering cross-section and for a natural sample, presence of different isotopes of the same element in the sample.

Since neutrons interact with the nuclear potential, the scattering cross-section varies with the atomic number of the element in question. A very prominent example is hydrogen and its isotope deuterium. The total cross-section for hydrogen is over 10 times that of deuterium, mostly due to the large incoherent scattering length of hydrogen. Metals tend to be rather transparent to neutrons, aluminum and zirconium being the two best examples of this.

Incident particle energy dependence

Main article: Neutron temperature

U235 fission cross section

For a given target and reaction, the cross section is strongly dependent on the neutron speed. In the extreme case, the cross section can be, at low energies, either null (the energy for which the cross section becomes significant is called threshold energy) or, on the contrary, much larger than the cross section at high energies.

Therefore, a cross section should be defined either at a given energy or should be averaged in an energy range (or group). See here for more details.

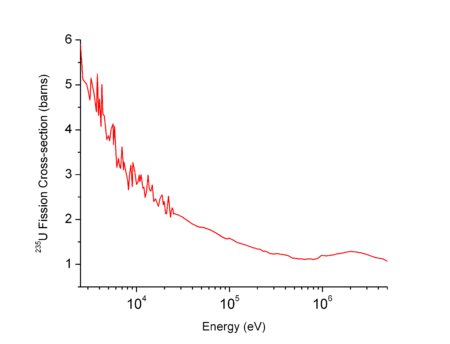
As an example, the plot on the right shows that the fission cross section of the uranium 235 is low at high neutron energies but becomes higher at low energies. Such physical constraint explains why most of the operational nuclear reactors use a neutron moderator to reduce the energy of the neutron and thus increase the probability of fission, essential to produce energy and sustain the chain reaction.

Target temperature dependence

Cross sections are usually measured at 20°C. To account for the dependence with temperature of the medium (viz. the target), the following formula is used ^[2]:

$\sigma = \sigma_0 \, \left(\frac{T_0}{T} \right)^\frac{1}{2}$

Where σ is the cross section at temperature T and σ₀ the cross section at temperature T₀ (T and T₀ in Kelvin)

Link to reaction rate and interpretation

Interpretation of the reaction rate with the help of the cross section

Let us imagine a spherical target (in grey in the figure) and a beam of particles (in blue) “flying” at speed v (vector in black) in the direction of the target. We want to know how many particles impact it during time interval dt. To achieve it, the particles have to be in the cylinder in green in the figure (volume V). The base of the cylinder is the geometrical cross section of the target perpendicular to the beam (surface σ in red) and its height the length travelled by the particles during dt (length v dt):

$V = \sigma \, v \, dt$

Noting n the number of particles per unit volume, there are n V particles in the volume V, which will, per definition of V, undergo a reaction. Noting r the reaction rate onto one target, it gives:

$r \, dt = n \, V = n \, \sigma \, v \, dt$

It follows directly from the definition of the neutron flux^[2] Φ = n v:

$r = \sigma \, \Phi$

Assuming that there is not one but N targets per unit volume, the reaction rate R per unit volume is:

$R = N \, r = N \, \Phi \, \sigma$

Knowing that the typical nuclear radius r is of the order of 10^-12 cm, the expected nuclear cross section is of the order of π r² or roughly 10^-24 cm² (thus justifying the definition of the barn). However, if measured experimentally (σ = R / (Φ N), the experimental cross sections vary enormously. As an example, for slow neutrons absorbed by the (n, γ) reaction the cross section in some cases is as much as 1,000 barns, while the cross sections for transmutations by gamma-ray absorption are in the neighborhood of 0.001 barn (See here for more example of cross sections).

The “nuclear cross section” is consequently a purely conceptual quantity representing how big should be the atom to be consistent with this simple mechanical model.

Continuous versus average cross section

Cross sections depend strongly on the incoming particle speed. In the case of a beam with multiple particle speeds, the reaction rate R is integrated over the whole range of energy:

$R = \int_E N \, \Phi (E) \, \sigma (E) \, dE$

Where σ(E) is the continuous cross section, Φ(E) the differential flux and N the target atom density.

In order to obtain a formulation equivalent to the mono energetic case, an average cross section is defined:

$\sigma =\frac{\int_E \Phi (E) \, \sigma (E) \, dE }{\int_E \Phi (E) \, dE}=\frac{\int_E \Phi (E) \, \sigma (E) \, dE}{\Phi}$

Where Φ= $\int$ Φ(E) dE is the integral flux.

Using the definition of the integral flux Φ and the average cross section σ, the same formulation as before is found:

$R = N \, \Phi \, \sigma$

Microscopic versus macroscopic cross section

Up to now, the cross section referred to in this article corresponds to the microscopic cross section σ. However, it is possible to define the macroscopic cross section^[2] Σ which corresponds to the total “equivalent area” of all target particles per unit volume:

$\Sigma = N \, \sigma$

where N is the atomic density of target.

Therefore, since the cross section can be expressed in cm² and the density in cm^-3, the macroscopic cross section is usually expressed in cm^-1. Using equation derived in #Link to reaction rate and interpretation, the reaction rate per unit volume R can be derived using only the neutron flux Φ and the macroscopic cross section Σ:

$R = \Sigma \, \Phi$

Mean free path

The aim of this paragraph is to evaluate the “mean free path” λ of a random particle, that is to say the average length travelled between two interactions.

The total length L that non perturbed particles travel during a time interval dt in a volume dV is simply the product of the length l covered by each particle during this time with the number of particles N in this volume:

$L = l \, N$

Noting v the speed of the particles and n is the number of particles per unit volume:

$l = v \, dt$

$N = n \, dV$

It follows:

$L = v \, dt \, n \, dV$

Using the definition of the neutron flux^[2] Φ

$\Phi = n \, v$

It follows:

$L = \Phi \, dt \, dV$

This average length L is however valid only for unperturbed particles. To account for the interactions, L is divided by the total number of reactions R to obtain the average length between each collision λ:

$\lambda = \frac{L}{R}= \frac{\Phi \, dt \, dV}{R}$

From #Microscopic versus macroscopic cross section:

$R = \Phi \, \Sigma \, dt \, dV$

It follows:

$\lambda = \frac{1}{\Sigma}$

where λ is the mean free path and Σ is the macroscopic cross section.

Within stars

Because lithium-8 and beryllium-12 form natural stopping points on the table of isotopes for hydrogen fusion it is believed that all of the higher elements are formed in very hot stars where higher orders of fusion predominate. A star like the Sun produces energy by the fusion of simple H-1 into helium-4 through a series of reactions. It is believed that when the inner core exhausts its H-1 fuel the sun will contract, slightly increasing its core temperature until He-4 can fuse and become the main fuel supply. Pure He-4 fusion leads to Be-8, which decays back to 2 He-4 therefore the He-4 must fuse with isotopes either more or less massive than itself to result in an energy producing reaction. When He-4 fuses with H-2 or H-3 it forms stable isotopes Li-6 and Li-7 respectively. The higher order isotopes between Li-8 and C-12 are synthesized by similar reactions between hydrogen, helium and lithium isotopes.

Typical cross sections

In the following, some cross sections which are of importance in a nuclear reactor are given. The thermal cross-section is averaged using a Maxwellian spectrum and the fast cross section is averaged using the uranium-235 fission spectrum. The cross sections are taken from the Jeff-3.1.1 library using Janis software ^[3].

		Thermal cross section (barn)			Fast cross section (barn)
		Scattering	Capture	Fission	Scattering	Capture	Fission
Moderator	H-1	2E+1	2E-1	-	4E+0	4E-5	-
	H-2	4E+0	3E-4	-	3E+0	7E-6	-
	C (nat)	5E+0	2E-3	-	2E+0	1E-5	-
Structural materials, others	Zr-90	5E+0	6E-3	-	5E+0	6E-3	-
	Fe-56	1E+1	2E+0	-	2E+1	3E-3	-
	Cr-52	3E+0	5E-1	-	3E+0	2E-3	-
	Ni-58	2E+1	3E+0	-	3E+0	8E-3	-
	0-16	4E+0	1E-4	-	3E+0	3E-8	-
Absorber	B-10	2E+0	2E+3	-	2E+0	4E-1	-
	Cd-113	1E+2	3E+4	-	4E+0	5E-2	-
	Xe-135	4E+5	2E+6	-	5E+0	8E-4	-
	In-115	2E+0	1E+2	-	4E+0	2E-1	-
Fuel	U-235	1E+1	6E+1	3E+2	4E+0	9E-2	1E+0
	U-238	9E+0	2E+0	2E-5	5E+0	7E-2	3E-1
	Pu-239	8E+0	4E-2	7E-2	5E+0	5E-2	2E+0

External links

• Neutron scattering lengths and cross-sections
• Periodic Table of Elements: Sorted by Cross Section (Thermal Neutron Capture)

References

1. ^ "ENDF/B-VII Incident-Neutron Data". T2.lanl.gov. 2007-07-15. http://t2.lanl.gov/data/neutron7.html. Retrieved 2011-11-08. 
2. ^ ^{a b c d e} DOE Fundamentals Handbook, Nuclear Physics and Reactor Theory, DOE-HDBK-1019/1-93 http://www.hss.doe.gov/nuclearsafety/techstds/docs/handbook/h1019v1.pdf
3. ^ Janis 3.3, http://www.oecd-nea.org/janis/