Nelder–Mead method

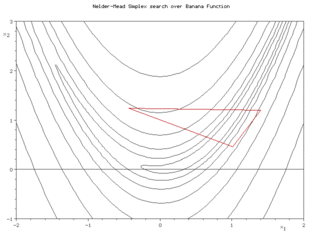
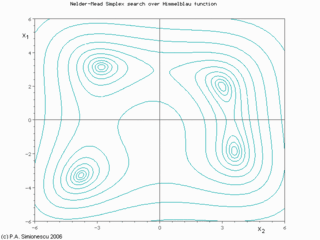
Nelder–Mead simplex search over the Rosenbrock banana function (above) and Himmelblau's function (below)

See simplex algorithm for Dantzig's algorithm for the problem of linear optimization.

The Nelder–Mead method or downhill simplex method or amoeba method is a commonly used nonlinear optimization technique, which is a well-defined numerical method for twice differentiable and unimodal problems. However, the Nelder–Mead technique is a heuristic search method that can converge to non-stationary points^[1] on problems that can be solved by alternative methods.^[2]

The Nelder–Mead technique was proposed by John Nelder & Roger Mead (1965) ^[3] and is a technique for minimizing an objective function in a many-dimensional space.

Overview

The method uses the concept of a simplex, which is a special polytope of N + 1 vertices in N dimensions. Examples of simplices include a line segment on a line, a triangle on a plane, a tetrahedron in three-dimensional space and so forth.

The method approximates a local optimum of a problem with N variables when the objective function varies smoothly and is unimodal.

For example, a suspension bridge engineer has to choose how thick each strut, cable, and pier must be. Clearly these all link together, but it is not easy to visualize the impact of changing any specific element. The engineer can use the Nelder–Mead method to generate trial designs which are then tested on a large computer model. As each run of the simulation is expensive, it is important to make good decisions about where to look.

Nelder–Mead generates a new test position by extrapolating the behavior of the objective function measured at each test point arranged as a simplex. The algorithm then chooses to replace one of these test points with the new test point and so the technique progresses. The simplest step is to replace the worst point with a point reflected through the centroid of the remaining N points. If this point is better than the best current point, then we can try stretching exponentially out along this line. On the other hand, if this new point isn't much better than the previous value, then we are stepping across a valley, so we shrink the simplex towards a better point.

Unlike modern optimization methods, the Nelder–Mead heuristic can converge to a non-stationary point unless the problem satisfies stronger conditions than are necessary for modern methods.^[1] Modern improvements over the Nelder–Mead heuristic have been known since 1979.^[2]

Many variations exist depending on the actual nature of the problem being solved. A common variant uses a constant-size, small simplex that roughly follows the gradient direction (which gives steepest descent). Visualize a small triangle on an elevation map flip-flopping its way down a valley to a local bottom. This method is also known as the Flexible Polyhedron Method. This, however, tends to perform poorly against the method described in this article because it makes small, unnecessary steps in areas of little interest.

One possible variation of the NM algorithm

• 1. Order according to the values at the vertices:

$f(\textbf{x}_{1}) \leq f(\textbf{x}_{2}) \leq \cdots \leq f(\textbf{x}_{n+1})$

• 2. Calculate x_o, the center of gravity of all points except x_{n + 1}.

• 3. Reflection

Compute reflected point $\textbf{x}_r = \textbf{x}_o + \alpha (\textbf{x}_o - \textbf{x}_{n+1})$

If the reflected point is better than the second worst, but not better than the best, i.e.: $f(\textbf{x}_{1}) \leq f(\textbf{x}_{r}) < f(\textbf{x}_{n})$,

then obtain a new simplex by replacing the worst point x_{n + 1} with the reflected point x_r, and go to step 1.

• 4. Expansion

If the reflected point is the best point so far, $f(\textbf{x}_{r}) < f(\textbf{x}_{1}),$

then compute the expanded point $\textbf{x}_{e} = \textbf{x}_o + \gamma (\textbf{x}_o - \textbf{x}_{n+1})$

If the expanded point is better than the reflected point, $f(\textbf{x}_{e}) < f(\textbf{x}_{r})$

then obtain a new simplex by replacing the worst point x_{n + 1} with the expanded point x_e, and go to step 1.

Else obtain a new simplex by replacing the worst point x_{n + 1} with the reflected point x_r, and go to step 1.

Else (i.e. reflected point is not better than second worst) continue at step 5.

• 5. Contraction

Here, it is certain that $f(\textbf{x}_{r}) \geq f(\textbf{x}_{n})$

Compute contracted point $\textbf{x}_{c} = \textbf{x}_{n+1}+\rho(\textbf{x}_{o}-\textbf{x}_{n+1})$

If the contracted point is better than the worst point, i.e. $f(\textbf{x}_{c}) < f(\textbf{x}_{n+1})$

then obtain a new simplex by replacing the worst point x_{n + 1} with the contracted point x_c, and go to step 1.

Else go to step 6.

• 6. Reduction

For all but the best point, replace the point with

$x_{i} = x_{1} + \sigma(x_{i} - x_{1}) \text{ for all i } \in\{2,\dots,n+1\}$. go to step 1.

Note: α, γ, ρ and σ are respectively the reflection, the expansion, the contraction and the shrink coefficient. Standard values are α = 1, γ = 2, ρ = 1 / 2 and σ = 1 / 2.

For the reflection, since x_{n + 1} is the vertex with the higher associated value among the vertices, we can expect to find a lower value at the reflection of x_{n + 1} in the opposite face formed by all vertices point x_i except x_{n + 1}.

For the expansion, if the reflection point x_r is the new minimum along the vertices we can expect to find interesting values along the direction from x_o to x_r.

Concerning the contraction: If f(x_r) > f(x_n) we can expect that a better value will be inside the simplex formed by all the vertices x_i.

The initial simplex is important, indeed, a too small initial simplex can lead to a local search, consequently the NM can get more easily stuck. So this simplex should depend on the nature of the problem.

See also

• Conjugate gradient method
• Levenberg–Marquardt algorithm
• Broyden–Fletcher–Goldfarb–Shanno or BFGS method
• Differential evolution

References

1. ^ ^{a b}
   • Powell, Michael J. D. 1973. ”On Search Directions for Minimization Algorithms.” Mathematical Programming 4: 193—201.
   • McKinnon, K.I.M. (1999). "Convergence of the Nelder–Mead simplex method to a non-stationary point". SIAM J Optimization 9: 148–158. doi:10.1137/S1052623496303482.  (algorithm summary online).
2. ^ ^{a b}
   • Yu, Wen Ci. 1979. “Positive basis and a class of direct search techniques”. Scientia Sinica [Zhongguo Kexue]: 53—68.
   • Yu, Wen Ci. 1979. “The convergent property of the simplex evolutionary technique”. Scientia Sinica [Zhongguo Kexue]: 69–77.
   • Kolda, Tamara G.; Lewis, Robert Michael; Torczon, Virginia (2003). "Optimization by direct search: new perspectives on some classical and modern methods". SIAM Rev. 45: 385–482. doi:10.1137/S003614450242889. 
   • Lewis, Robert Michael; Shepherd, Anne; Torczon, Virginia (2007). "Implementing generating set search methods for linearly constrained minimization". SIAM J. Sci. Comput. 29: 2507—2530. doi:10.1137/050635432. 
3. ^ Nelder, John A.; R. Mead (1965). "A simplex method for function minimization". Computer Journal 7: 308–313. doi:10.1093/comjnl/7.4.308. 

Further reading

• Avriel, Mordecai (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN 0-486-43227-0.

• Coope, I. D.; C.J. Price, 2002. “Positive bases in numerical optimization”, Computational Optimization & Applications, Vol. 21, No. 2, pp. 169–176, 2002.

• Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). "Section 10.5. Downhill Simplex Method in Multidimensions". Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8. http://apps.nrbook.com/empanel/index.html#pg=502. 

External links

• Nelder–Mead (Simplex) Method
• Nelder–Mead Search for a Minimum
• John Burkardt: Nelder–Mead code in Matlab - note that a variation of the Nelder-Mead method is also implemented by the Matlab function fminsearch.
• Nelder–Mead online for the calibration of the SABR model - Application in Finance.