- Genus–differentia definition
-
Part of a series on Aristotelianism  IdeasCorrespondence theory of truth
IdeasCorrespondence theory of truth
hexis
virtue ethics (golden mean)
four causes
telos
phronesis
eudaimonia
arete
temporal finitism
antiperistasis
nature
potentiality and actuality
universals (substantial form)
hylomorphism
mimesis
substances (ousia) and accidents
essence
category of being
magnanimity
sensus communis
rational animal
genus-differentia definitionInfluences and followersPlato
Alexander the Great
Theophrastus
Avicenna
Averroes
Maimonides
St. Thomas Aquinas
Alasdair MacIntyre
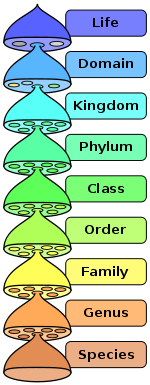
Martha Nussbaum Philosophy portalThe hierarchy of biological classification's eight major taxonomic ranks, which is an example of definition by genus and differentia. Intermediate minor rankings are not shown.
Philosophy portalThe hierarchy of biological classification's eight major taxonomic ranks, which is an example of definition by genus and differentia. Intermediate minor rankings are not shown.
A genus–differentia definition is a type of intensional definition, and it is composed of two parts:
- a genus (or family): An existing definition that serves as a portion of the new definition; all definitions with the same genus are considered members of that genus.
- the differentia: The portion of the new definition that is not provided by the genera.
For example, consider these two definitions:
- a triangle: A plane figure that has 3 straight bounding sides.
- a quadrilateral: A plane figure that has 4 straight bounding sides.
Those definitions can be expressed as one genus and two differentiae:
- one genus: A plane figure.
- two differentiae:
- the differentia for a triangle: that has 3 straight bounding sides.
- the differentia for a quadrilateral: that has 4 straight bounding sides.
Contents
Differentiation and Abstraction
This process of producing new definitions by extending existing definitions is commonly known as differentiation (and also as derivation). The reverse process, by which just part of an existing definition is used itself as a new definition, is called abstraction; the new definition is called an abstraction and it is said to have been abstracted away from the existing definition.
For instance, consider the following:
- a square: a quadrilateral that has interior angles which are all right angles, and that has bounding sides which all have the same length.
A part of that definition may be singled out (using parentheses here):
- a square: (a quadrilateral that has interior angles which are all right angles), and that has bounding sides which all have the same length.
and with that part, an abstraction may be formed:
- a rectangle: a quadrilateral that has interior angles which are all right angles.
Then, the definition of 'square' may be recast with that abstraction as its genus:
- a square: a rectangle that has bounding sides which all have the same length.
Similarly, the definition of 'square' may be rearranged and another portion singled out:
- a square: (a quadrilateral that has bounding sides which all have the same length), and that has interior angles which are all right angles.
leading to the following abstraction:
- a rhombus: a quadrilateral that has bounding sides which all have the same length.
Then, the definition of 'square' may be recast with that abstraction as its genus:
- a square: a rhombus that has interior angles which are all right angles.
In fact, the definition of a 'square' may be recast in terms of both of the abstractions, where one acts as the genus and the other acts as the differentia:
- a square: a rectangle that is a rhombus.
- a square: a rhombus that is a rectangle.
Hence, abstraction is crucial in simplifying definitions.
Multiplicity
When multiple definitions could serve equally well, then all such definitions apply simultaneously. Thus, a 'square' is a member of both the genus 'rectangle' and the genus 'rhombus'. In such a case, it is notationally convenient to consolidate the definitions into one definition that is expressed with multiple genera (and possibly no differentia, as in the following):
- a square: a rectangle and a rhombus.
or completely equivalently:
- a square: a rhombus and a rectangle.
More generally, a definition expressed as having n > 1 genera can be recast as at least n equivalent definitions, each of which has just one genus. Thus, the following:
- a Definition: a Genus1 and a Genus2 and a Genus3 and a ... and a Genusn-1 and a Genusn that has some non-genus Differentia.
could be recast as:
- a Definition: a Genus1 that is a Genus2 and that is a Genus3 and that is a ... and that is a Genusn − 1 and that is a Genusn that has some non-genus Differentia.
- a Definition: a Genus2 that is a Genus1 and that is a Genus3 and that is a ... and that is a Genusn − 1 and that is a Genusn that has some non-genus Differentia.
- a Definition: a Genus3 that is a Genus1 and that is a Genus2 and that is a ... and that is a Genusn − 1 and that is a Genusn that has some non-genus Differentia.
- ...
- a Definition: a Genusn − 1 that is a Genus1 and that is a Genus2 and that is a Genus3 and that is a ... and that is a Genusn that has some non-genus Differentia.
- a Definition: a Genusn that is a Genus1 and that is a Genus2 and that is a Genus3 and that is a ... and that is a Genusn − 1 that has some non-genus Differentia.
Structure
In other words, a genus of a definition provides a means by which to specify an is-a relationship:
- A square is a rectangle, which is a quadrilateral, which is a plane figure, which is a ...
- A square is a rhombus, which is a quadrilateral, which is a plane figure, which is a ...
- A square is a quadrilateral, which is a plane figure, which is a ...
- A square is a plane figure, which is a ...
- A square is a ...
The non-genus portion of the differentia of a definition provides a means by which to specify a has-a relationship:
- A square has interior angles which are all right angles.
- A square has bounding sides which all have the same length.
- A square has 4 straight bounding sides.
- ...
When a system of definitions is constructed with genera and differentiae, the definitions can be thought of as nodes forming a hierarchy or—more generally—a directed acyclic graph; a node that has no predecessor is a most general definition; each node along a directed path is more differentiated (or more derived) than any one of its predecessors, and a node with no successor is a most differentiated (or a most derived) definition. When a definition, S, is the tail of all of its successors (that is, S has at least one successor and each direct successor of S is a most differentiated definition), then S is often called a species and each direct successor of S is often called an individual or an entity; the differentia of an individual is called an identity. For instance:
- [the] Mfwitten: a Wikipedia user with the account name 'Mfwitten'.
As in that example, the identity itself (or some part of it) is often used to refer to the entire individual, a phenomenon that is known in linguistics as a pars pro toto synechdoche.
Examples
This can be clarified with a hackneyed example. Suppose we wanted to define the phrase human being. Following the ancient Greeks (Socrates and his successors) and modern biologists, we say that human being is a species and that each individual person is a member of the species human being. So we ask what the genus, or general category, of the species is; the Greeks (but not the biologists) would say that the genus is animal. What is the differentia of the species, that is, the distinguishing characteristic of human being that other animals do not have? The Greeks said it is rationality; thus, Aristotle said, A human being is a rational animal.[1]
However, the use of the genus–differentia definition is by no means restricted to science. Rather, it is the natural thing to do if you are to explain the meaning of a particular word to someone. With this, the "classical" type of definition (definitio fit per genus proximum et differentiam specificam), you use the copula (is, are) after the definiendum (just as if you were using an equals sign in a mathematical equation) and then go on to explain the definiendum by using the appropriate generic term plus those characteristics specific to the thing you are describing, thereby narrowing down the meaning until the definiendum can no longer be confused with anything else; here are some examples from everyday life:
- A paperweight is a small, heavy object which is placed on papers to prevent them from being scattered.
- paperweight—definiendum
- object—generic term
- small but heavy, placed on papers, reason why—differentiae specificae
- Homesickness is the feeling of unhappiness you may experience when you are away from home and miss your home and your family very much.
- Subtitles are the printed translation that you can read at the bottom of the screen when you are watching a foreign film.
- In film and broadcasting, a soundbite is a very short piece of footage taken from a longer speech or interview in which someone with authority says something which is considered by those who edit the speech or interview to be a most important point.
- A mosque is a building, often with high towers and domes, where Muslims go to worship.
References
Categories:- Definition
- Philosophy of language
- Dichotomies
Wikimedia Foundation. 2010.