Harmonic seventh

harmonic seventh

Inverse	Septimal major second
Name
Other names	Septimal minor seventh, Subminor seventh
Abbreviation	m7
Size
Semitones	~9.7
Interval class	~2.3
Just interval	7:4[1]
Cents
Equal temperament	1000
24 equal temperament	950
Just intonation	968.826

Harmonic seventh  Play (help·info), septimal seventh.

Inverse, septimal major second on B7♭  Play (help·info).

The harmonic seventh interval  play (help·info), also known as the septimal minor seventh^[2][3], or subminor seventh^[4][5][6], is one with an exact 7:4 ratio^[7] (about 969 cents).^[8] This is somewhat narrower than and is "sweeter in quality" than an "ordinary"^[9] minor seventh, which has a just-intonation ratio of 9:5^[10] (1017.596 cents), or an equal-temperament ratio of 1000 cents (2^5/6:1). The harmonic seventh may be derived from the harmonic series as the interval between the seventh harmonic and the fourth harmonic.

Composer Ben Johnston uses a small "7" as an accidental to indicate a note is lowered 49 cents (1018-969=49), or an upside-down "7" to indicate a note is raised 49 cents. Thus, in C major, "the seventh partial," or harmonic seventh, is notated as ♭ B with "7" written above the flat.^[11][12] The harmonic seventh is also used by Barbershop Quartet singers when they tune dominant seventh chords (harmonic seventh chord), and is an essential aspect of the Barbershop style.

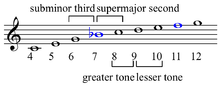Origin of large and small seconds and thirds in harmonic series^[13].

The harmonic seventh differs from the augmented sixth by 224/225 (7.71 cents), or about one-third of a comma.^[14] The harmonic seventh note is about a sixth-tone flatter than an equal tempered minor seventh (≈ 31 cents). When this flatter seventh is used, the dominant seventh chord's "need to resolve" down a fifth is weak or non-existent. This chord is often used on the tonic (written as I7) and functions as a "fully resolved" final chord.^[15]

Notes

1. ^ Haluska, Jan (2003). The Mathematical Theory of Tone Systems, p.xxiii. ISBN 0824747143. Harmonic seventh.
2. ^ Gann, Kyle (1998). "Anatomy of an Octave", Just Intonation Explained.
3. ^ Partch, Harry (1979). Genesis of a Music, p.68. ISBN 030680106X.
4. ^ Hermann L. F Von Helmholtz (2007). On the Sensations of Tone, p.456. ISBN 1602066396.
5. ^ Royal Society (Great Britain) (1880, digitized Feb 26, 2008). Proceedings of the Royal Society of London, Volume 30, p.531. Harvard University.
6. ^ Society of Arts (Great Britain) (1877, digitized Nov 19, 2009). Journal of the Society of Arts, Volume 25, p.670. The Society.
7. ^ Andrew Horner, Lydia Ayres (2002). Cooking with Csound: Woodwind and Brass Recipes, p.131. ISBN 0895795078.
8. ^ Bosanquet, Robert Holford Macdowall (1876). An elementary treatise on musical intervals and temperament, pp. 41-42. Diapason Press; Houten, The Netherlands. ISBN 90-70907-12-7.
9. ^ "On Certain Novel Aspects of Harmony", p.119. Eustace J. Breakspeare. Proceedings of the Musical Association, 13th Sess., (1886 - 1887), pp. 113-131. Published by: Oxford University Press on behalf of the Royal Musical Association.
10. ^ "The Heritage of Greece in Music", p.89. Wilfrid Perrett. Proceedings of the Musical Association, 58th Sess., (1931 - 1932), pp. 85-103. Published by: Oxford University Press on behalf of the Royal Musical Association.
11. ^ Douglas Keislar; Easley Blackwood; John Eaton; Lou Harrison; Ben Johnston; Joel Mandelbaum; William Schottstaedt. p.193. "Six American Composers on Nonstandard Tunnings", Perspectives of New Music, Vol. 29, No. 1. (Winter, 1991), pp. 176-211.
12. ^ Fonville, John. "Ben Johnston's Extended Just Intonation: A Guide for Interpreters", Perspectives of New Music, Vol. 29, No. 2 (Summer, 1991), pp. 106-137.
13. ^ Leta E. Miller, ed. (1988). Lou Harrison: Selected keyboard and chamber music, 1937-1994, p.xliii. ISBN 9780895794147.
14. ^ "On Some Points in the Harmony of Perfect Consonances", p.153. R. H. M. Bosanquet. Proceedings of the Musical Association, 3rd Sess., (1876 - 1877), pp. 145-153. Published by: Oxford University Press on behalf of the Royal Musical Association.
15. ^ Mathieu, W.A. (1997). Harmonic Experience, pp. 318-319. Inner Traditions International; Rochester, Vermont. ISBN 0-89281-560-4.