- Schulze method
-
Part of the Politics series Electoral methods Single-winner Multiple-winner - Proportional representation
- Party-list (open · closed · mixed · local)
- Single transferable vote (CPO-STV · Schulze STV · Wright system)
- Semi-proportional representation
Proxy voting Random selection Social choice theory - Arrow's theorem
- Gibbard–Satterthwaite theorem
- Voting system criteria
Politics portal The Schulze method is a voting system developed in 1997 by Markus Schulze that selects a single winner using votes that express preferences. The method can also be used to create a sorted list of winners. The Schulze method is also known as Schwartz Sequential Dropping (SSD), Cloneproof Schwartz Sequential Dropping (CSSD), the Beatpath Method, Beatpath Winner, Path Voting, and Path Winner.
The Schulze method is a Condorcet method, which means the following: if there is a candidate who is preferred over every other candidate in pairwise comparisons, then this candidate will be the winner when the Schulze method is applied.
Currently, the Schulze method is the most widespread Condorcet method (list). The Schulze method is used by several organizations including Wikimedia, Debian, Gentoo, and Software in the Public Interest.
The output of the Schulze method (defined below) gives an ordering of candidates. Therefore, if several positions are available, the method can be used for this purpose without modification, by letting the k top-ranked candidates win the k available seats. Furthermore, for proportional representation elections, a single transferable vote variant has been proposed.
Contents
Description of the method
Ballot
The input to the Schulze method is the same as for other preferential single-winner election methods: each voter must furnish an ordered preference list on candidates where ties are allowed.
One typical way for voters to specify their preferences on a ballot (see left) is as follows. Each ballot lists all the candidates, and each voter ranks this list in order of preference using numbers: the voter places a '1' beside the most preferred candidate(s), a '2' beside the second-most preferred, and so forth. Each voter may optionally
- give the same preference to more than one candidate. This indicates that this voter is indifferent between these candidates.
- use non-consecutive numbers to express preferences. This has no impact on the result of the elections, since only the order in which the candidates are ranked by the voter matters, and not the absolute numbers of the preferences.
- keep candidates unranked. When a voter doesn't rank all candidates, then this is interpreted as if this voter (i) strictly prefers all ranked to all unranked candidates, and (ii) is indifferent among all unranked candidates.
Schulze Method
Let d[V,W] be the number of voters who prefer candidate V to candidate W.
A path from candidate X to candidate Y of strength p is a sequence of candidates C(1),...,C(n) with the following properties:
- C(1) = X and C(n) = Y.
- For all i = 1,...,(n-1): d[C(i),C(i+1)] > d[C(i+1),C(i)].
- For all i = 1,...,(n-1): d[C(i),C(i+1)] ≥ p.
p[A,B], the strength of the strongest path from candidate A to candidate B, is the maximum value such that there is a path from candidate A to candidate B of that strength. If there is no path from candidate A to candidate B at all, then p[A,B] = 0.
Candidate D is better than candidate E if and only if p[D,E] > p[E,D].
Candidate D is a potential winner if and only if p[D,E] ≥ p[E,D] for every other candidate E.
It can be proven that p[X,Y] > p[Y,X] and p[Y,Z] > p[Z,Y] together imply p[X,Z] > p[Z,X].[1]:§4.1 Therefore, it is guaranteed (1) that the above definition of "better" really defines a transitive relation and (2) that there is always at least one candidate D with p[D,E] ≥ p[E,D] for every other candidate E.
Example
Consider the following example, in which 45 voters rank 5 candidates.
- 5 ACBED (meaning, 5 voters have order of preference: A > C > B > E > D)
- 5 ADECB
- 8 BEDAC
- 3 CABED
- 7 CAEBD
- 2 CBADE
- 7 DCEBA
- 8 EBADC
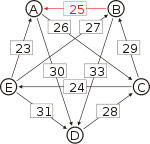
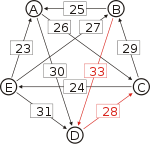
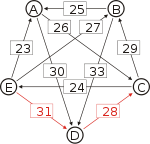
First, we compute the pairwise preferences. For example, in comparing A and B pairwise, there are 5+5+3+7=20 voters who prefer A to B, and 8+2+7+8=25 voters who prefer B to A. So d[A, B] = 20 and d[B, A] = 25. The full set of pairwise preferences is:
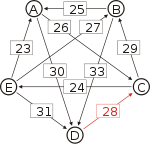
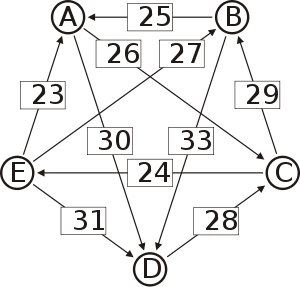 Directed graph labeled with pairwise preferences d[*, *]
Directed graph labeled with pairwise preferences d[*, *]
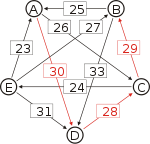
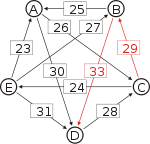
Matrix of pairwise preferences d[*,A] d[*,B] d[*,C] d[*,D] d[*,E] d[A,*] 20 26 30 22 d[B,*] 25 16 33 18 d[C,*] 19 29 17 24 d[D,*] 15 12 28 14 d[E,*] 23 27 21 31 To help visualize the strongest paths, the diagram on the right-hand side shows an arrow from A to B with label d[A, B], in the style of a directed graph. (To avoid cluttering the diagram we only draw the majority of voters)
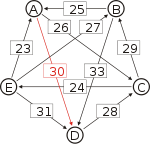
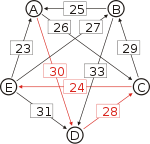
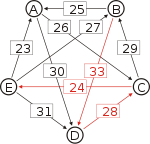
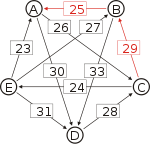
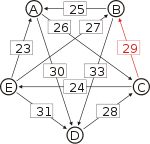
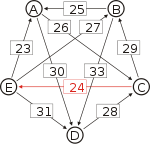
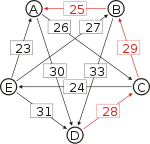
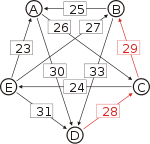
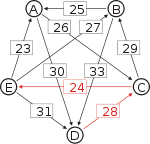
Recall that the strength of a path is the strength of its weakest link. One example of computing the strongest path strength is p[B, D] = 33: the strongest path from B to D is the direct path (B, D) which has strength 33. For contrast, let us also compute p[A, C]. The strongest path from A to C is not the direct path (A, C) of strength 26, rather the strongest path is the indirect path (A, D, C) which has strength min(30, 28) = 28.
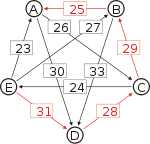
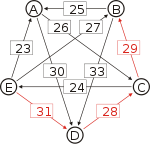
For each pair of candidates X and Y, the following table shows the strongest path from candidate X to candidate Y in red, with the weakest link underlined.
Strongest paths ... to A ... to B ... to C ... to D ... to E from A ... A-(30)-D-(28)-C-(29)-B A-(30)-D-(28)-C A-(30)-D A-(30)-D-(28)-C-(24)-E from A ... from B ... B-(25)-A B-(33)-D-(28)-C B-(33)-D B-(33)-D-(28)-C-(24)-E from B ... from C ... C-(29)-B-(25)-A C-(29)-B C-(29)-B-(33)-D C-(24)-E from C ... from D ... D-(28)-C-(29)-B-(25)-A D-(28)-C-(29)-B D-(28)-C D-(28)-C-(24)-E from D ... from E ... E-(31)-D-(28)-C-(29)-B-(25)-A E-(31)-D-(28)-C-(29)-B E-(31)-D-(28)-C E-(31)-D from E ... ... to A ... to B ... to C ... to D ... to E Strengths of the strongest paths p[*,A] p[*,B] p[*,C] p[*,D] p[*,E] p[A,*] 28 28 30 24 p[B,*] 25 28 33 24 p[C,*] 25 29 29 24 p[D,*] 25 28 28 24 p[E,*] 25 28 28 31 Now we can determine the output of the Schulze method. Comparing A and B for example, since 28 = p[A,B] > p[B,A] = 25, for the Schulze method candidate A is better than candidate B. Another example is that 31 = p[E,D] > p[D,E] = 24, so candidate E is better than candidate D. Continuing in this way we get the Schulze ranking is E > A > C > B > D, and E wins. In other words, E wins since p[E,X] ≥ p[X,E] for every other candidate X.
Implementation
The only difficult step in implementing the Schulze method is computing the strongest path strengths. However, this is a well-known problem in graph theory sometimes called the widest path problem. One simple way to compute the strengths therefore is a variant of the Floyd–Warshall algorithm. The following pseudocode illustrates the algorithm.
-
# Input: d[i,j], the number of voters who prefer candidate i to candidate j. -
# Output: p[i,j], the strength of the strongest path from candidate i to candidate j. -
-
for i from 1 to C
-
for j from 1 to C
-
if (i <> j) then -
if (d[i,j] > d[j,i]) then -
p[i,j] := d[i,j] -
else -
p[i,j] := 0 -
-
for i from 1 to C
-
for j from 1 to C
-
if (i <> j) then -
for k from 1 to C -
if (i <> k and j <> k) then -
p[j,k] := max ( p[j,k], min ( p[j,i], p[i,k] ) )
This algorithm is efficient, and has running time proportional to C3 where C is the number of candidates. (This does not account for the running time of computing the d[*,*] values, which if implemented in the most straightforward way, takes time proportional to C2 times the number of voters.)
Ties and alternative implementations
When we allow users to have ties in their preferences, the outcome of the Schulze method naturally depends on how we interpret these ties in defining d[*,*]. Two natural choices are that d[A, B] represents either the number of voters who strictly prefer A to B (A>B), or the margin of (voters with A>B) minus (voters with B>A). But no matter how the ds are defined, the Schulze ranking has no cycles, and assuming the ds are unique it has no ties.[1]
Although ties in the Schulze ranking are unlikely,[2] they are possible. Schulze's original paper[1] proposed breaking ties in accordance with a voter selected at random, and iterating as needed.
An alternative, slower, way to describe the winner of the Schulze method is the following procedure:
- draw a complete directed graph with all candidates, and all possible edges between candidates
- iteratively [a] delete all candidates not in the Schwartz set (i.e. any candidate which cannot reach all others) and [b] delete the weakest link
- the winner is the last non-deleted candidate.
Satisfied and failed criteria
Satisfied criteria
The Schulze method satisfies the following criteria:
- Unrestricted domain
- Non-imposition (a.k.a. citizen sovereignty)
- Non-dictatorship
- Pareto criterion[1]:§4.3
- Monotonicity criterion[1]:§4.5
- Majority criterion
- Majority loser criterion
- Condorcet criterion
- Condorcet loser criterion
- Schwartz criterion
- Smith criterion[1]:§4.7
- Independence of Smith-dominated alternatives[1]:§4.7
- Mutual majority criterion
- Independence of clones[1]:§4.6
- Reversal symmetry[1]:§4.4
- Mono-append[3]
- Mono-add-plump[3]
- Resolvability criterion[1]:§4.2
- Polynomial runtime[1]:§2.3"
- Woodall's plurality criterion if winning votes are used for d[X,Y]
- Symmetric-completion[3] if margins are used for d[X,Y]
Failed criteria
Since the Schulze method satisfies the Condorcet criterion, it automatically fails the following criteria:
- Participation[1]:§3.4
- Consistency
- Invulnerability to compromising
- Invulnerability to burying
- Later-no-harm
Likewise, since the Schulze method is not a dictatorship and agrees with unanimous votes, Arrow's Theorem implies it fails the criterion
Comparison table
The following table compares the Schulze method with other preferential single-winner election methods:
Monotonic Condorcet Majority Condorcet loser Majority loser Mutual majority Smith ISDA Clone independence Reversal symmetry Polynomial time Participation, Consistency Schulze Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes No Ranked pairs Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes No Kemeny-Young Yes Yes Yes Yes Yes Yes Yes Yes No Yes No No Nanson No Yes Yes Yes Yes Yes Yes No No Yes Yes No Baldwin No Yes Yes Yes Yes Yes Yes No No No Yes No Instant-runoff voting No No Yes Yes Yes Yes No No Yes No Yes No Borda Yes No No Yes Yes No No No No Yes Yes Yes Bucklin Yes No Yes No Yes Yes No No No No Yes No Coombs No No Yes Yes Yes Yes No No No No Yes No MiniMax Yes Yes Yes No No No No No No No Yes No Plurality Yes No Yes No No No No No No No Yes Yes Anti-plurality Yes No No No Yes No No No No No Yes Yes Contingent voting No No Yes Yes Yes No No No No No Yes No Sri Lankan contingent voting No No Yes No No No No No No No Yes No Supplementary voting No No Yes No No No No No No No Yes No Dodgson No Yes Yes No No No No No No No No No The main difference between the Schulze method and the ranked pairs method (both of which have tick the same boxes in the above table) can be seen in this example:
Suppose the MinMax score of a set X of candidates is the strength of the strongest pairwise win of a candidate A ∉ X against a candidate B ∈ X. Then the Schulze method, but not the ranked pairs method, guarantees that the winner is always a candidate of the set with minimum MinMax score.[1]:§4.8 So, in some sense, the Schulze method minimizes the strongest pairwise win that has to be overturned when determining the winner.
History of the Schulze method
The Schulze method was developed by Markus Schulze in 1997. It was first discussed in public mailing lists in 1997–1998[4] and in 2000.[5] Subsequently, Schulze method users included Software in the Public Interest (2003),[6] Debian (2003),[7] Gentoo (2005),[8] TopCoder (2005),[9] Wikimedia (2008),[10] KDE (2008),[11] the Free Software Foundation Europe (2008),[12] the Pirate Party of Sweden (2009),[13] and the Pirate Party of Germany (2010).[14] In the French Wikipedia, the Schulze method was one of two multi-candidate methods approved by a majority in 2005,[15] and it has been used several times.[16]
In 2011, Schulze published the method in the academic journal Social Choice and Welfare.[1]
Use of the Schulze method
 sample ballot for Wikimedia's Board of Trustees elections
sample ballot for Wikimedia's Board of Trustees elections
The Schulze method is not currently used in parliamentary elections. However, it has been used for parliamentary primaries in the Swedish Pirate Party. It is also starting to receive support in other public organizations. Organizations which currently use the Schulze method are:
- Annodex Association [17]
- Blitzed [18]
- BoardGameGeek [19]
- Cassandra [20]
- Codex Alpe Adria [21]
- College of Marine Science [22]
- Computer Science Departmental Society for York University (HackSoc) [23]
- County Highpointers [24]
- Debian [7]
- Demokratische Bildung Berlin [25]
- Digital Freedom in Education and Youth [26]
- EnMasse Forums
- EuroBillTracker [27]
- European Democratic Education Conference (EUDEC) [28]
- Fair Trade Northwest [29]
- FFmpeg [30]
- Flemish Student Society of Leuven [31]
- Free Geek [32]
- Free Hardware Foundation of Italy [33]
- Free Software Foundation Europe (FSFE) [12]
- Gentoo Foundation [8]
- GNU Privacy Guard (GnuPG) [34]
- Gothenburg Hacker Space (GHS) [35]
- Graduate Student Organization at the State University of New York: Computer Science (GSOCS) [36]
- Haskell [37]
- Kanawha Valley Scrabble Club [38]
- KDE e.V. [11]
- Kingman Hall [39]
- Knight Foundation [40]
- Kumoricon [41]
- League of Professional System Administrators (LOPSA) [42]
- Libre-Entreprise [43]
- Lumiera/Cinelerra [44]
- Mathematical Knowledge Management Interest Group (MKM-IG) [45]
- Metalab [46]
- Music Television (MTV) [47]
- Neo [48]
- netznetz [49]
- Noisebridge [50]
- North Shore Cyclists (NSC) [51]
- OpenEmbedded [52]
- OpenStack [53]
- Park Alumni Society (PAS) [54]
- Pirate Party of Australia [55]
- Pirate Party of Austria [56]
- Pirate Party of Brazil
- Pirate Party of France [57]
- Pirate Party of Germany [14]
- Pirate Party of New Zealand [58]
- Pirate Party of Sweden [13]
- Pirate Party of Switzerland [59]
- Pitcher Plant of the Month
- Pittsburgh Ultimate [60]
- RPMrepo [61]
- Sender Policy Framework (SPF) [62]
- Software in the Public Interest (SPI) [6]
- Squeak [63]
- Students for Free Culture [64]
- Sugar Labs [65]
- Sverok [66]
- TopCoder [9]
- University of British Columbia Math Club [67]
- WikIAC [68]
- Wikimedia Foundation [10]
- Wikipedia in French,[15] Hebrew,[69] Hungarian,[70] and Russian.[71]
Notes
- ^ a b c d e f g h i j k l m n Markus Schulze, A new monotonic, clone-independent, reversal symmetric, and condorcet-consistent single-winner election method, Social Choice and Welfare, volume 36, number 2, page 267–303, 2011. Preliminary version in Voting Matters, 17:9-19, 2003.
- ^ Under reasonable probabilistic assumptions when the number of voters is much larger than the number of candidates
- ^ a b c Douglas R. Woodall, Properties of Preferential Election Rules, Voting Matters, issue 3, pages 8-15, December 1994
- ^ See:
- Markus Schulze, Condorect sub-cycle rule, October 1997 (In this message, the Schulze method is mistakenly believed to be identical to the ranked pairs method.)
- Mike Ossipoff, Party List P.S., July 1998
- Markus Schulze, Tiebreakers, Subcycle Rules, August 1998
- Markus Schulze, Maybe Schulze is decisive, August 1998
- Norman Petry, Schulze Method - Simpler Definition, September 1998
- Markus Schulze, Schulze Method, November 1998
- ^ See:
- Anthony Towns, Disambiguation of 4.1.5, November 2000
- Norman Petry, Constitutional voting, definition of cumulative preference, December 2000
- ^ a b Process for adding new board members, January 2003
- ^ a b See:
- ^ a b See:
- Gentoo Foundation Charter
- Aron Griffis, 2005 Gentoo Trustees Election Results, May 2005
- Lars Weiler, Gentoo Weekly Newsletter 23 May 2005
- Daniel Drake, Gentoo metastructure reform poll is open, June 2005
- Grant Goodyear, Results now more official, September 2006
- 2007 Gentoo Council Election Results, September 2007
- 2008 Gentoo Council Election Results, June 2008
- 2008 Gentoo Council Election Results, November 2008
- 2009 Gentoo Council Election Results, June 2009
- 2009 Gentoo Council Election Results, December 2009
- 2010 Gentoo Council Election Results, June 2010
- ^ a b See:
- 2006 TopCoder Open Logo Design Contest, November 2005
- 2006 TopCoder Collegiate Challenge Logo Design Contest, June 2006
- 2007 TopCoder High School Tournament Logo, September 2006
- 2007 TopCoder Arena Skin Contest, November 2006
- 2007 TopCoder Open Logo Contest, January 2007
- 2007 TopCoder Open Web Design Contest, January 2007
- 2007 TopCoder Collegiate Challenge T-Shirt Design Contest, September 2007
- 2008 TopCoder Open Logo Design Contest, September 2007
- 2008 TopCoder Open Web Site Design Contest, October 2007
- 2008 TopCoder Open T-Shirt Design Contest, March 2008
- ^ a b See:
- Jesse Plamondon-Willard, Board election to use preference voting, May 2008
- Mark Ryan, 2008 Wikimedia Board Election results, June 2008
- 2008 Board Elections, June 2008
- 2009 Board Elections, August 2009
- ^ a b section 3.4.1 of the Rules of Procedures for Online Voting
- ^ a b See:
- article 6 section 3 of the constitution
- Fellowship vote for General Assembly seats, March 2009
- And the winner of the election for FSFE's Fellowship GA seat is ..., June 2009
- ^ a b See:
- Inför primärvalen, October 2009
- Dags att kandidera till riksdagen, October 2009
- Råresultat primärvalet, January 2010
- ^ a b 11 of the 16 regional sections and the federal section of the Pirate Party of Germany are using LiquidFeedback for unbinding internal opinion polls. In 2010/2011, the Pirate Parties of Neukölln (link), Mitte (link), Steglitz-Zehlendorf (link), Lichtenberg (link), and Tempelhof-Schöneberg (link) adopted the Schulze method for its primaries. In 2011, the Pirate Party of Berlin adopted this method for its primaries (link).
- ^ a b Choix dans les votes
- ^ fr:Spécial:Pages liées/Méthode Schulze
- ^ Election of the Annodex Association committee for 2007, February 2007
- ^ Condorcet method for admin voting, January 2005
- ^ See:
- Important notice for Golden Geek voters, September 2007
- Golden Geek Awards 2008 - Nominations Open, August 2008
- Golden Geek Awards 2009 - Nominations Open, August 2009
- Golden Geek Awards 2010 - Nominations Open, September 2010
- Golden Geek Awards 2011 - Nominations Open, September 2011
- ^ Project Logo, October 2009
- ^ "Codex Alpe Adria Competitions". 0xaa.org. 2010-01-24. http://0xAA.org/competitions/. Retrieved 2010-05-08.
- ^ "Fellowship Guidelines" (PDF). http://www.marine.usf.edu/fellowships/Guidelines-and-Application-2011-2012.pdf. Retrieved 2011-06-01.
- ^ Report on HackSoc Elections, December 2008
- ^ Adam Helman, Family Affair Voting Scheme - Schulze Method
- ^ appendix 1 of the constitution
- ^ Logo Competition, May 2009
- ^ See:
- Candidate cities for EBTM05, December 2004
- Meeting location preferences, December 2004
- Date for EBTM07 Berlin, January 2007
- Vote the date of the Summer EBTM08 in Ljubljana, January 2008
- New Logo for EBT, August 2009
- ^ "Guidance Document". Eudec.org. 2009-11-15. http://www.eudec.org/wiki/index.php?title=Guidance_Document&oldid=797. Retrieved 2010-05-08.
- ^ article XI section 2 of the bylaws
- ^ Democratic election of the server admins, July 2010
- ^ article 51 of the statutory rules
- ^ Voters Guide, September 2011
- ^ See:
- Eletto il nuovo Consiglio nella Free Hardware Foundation, June 2008
- Poll Results, June 2008
- ^ GnuPG Logo Vote, November 2006
- ^ §14 of the bylaws
- ^ "User Voting Instructions". Gso.cs.binghamton.edu. http://gso.cs.binghamton.edu/index.php/Voting. Retrieved 2010-05-08.
- ^ Haskell Logo Competition, March 2009
- ^ A club by any other name ..., April 2009
- ^ See:
- Ka-Ping Yee, Condorcet elections, March 2005
- Ka-Ping Yee, Kingman adopts Condorcet voting, April 2005
- ^ Knight Foundation awards $5000 to best created-on-the-spot projects, June 2009
- ^ See:
- Mascot 2007 contest, July 2006
- Mascot 2008 and cover 2007 contests, May 2007
- Mascot 2009 and program cover 2008 contests, April 2008
- Mascot 2010 and program cover 2009 contests, May 2009
- Mascot 2011 and book cover 2010 contests, May 2010
- Mascot 2012 and book cover 2011 contests, May 2011
- ^ article 8.3 of the bylaws
- ^ See:
- ^ Lumiera Logo Contest, January 2009
- ^ The MKM-IG uses Condorcet with dual dropping. That means: The Schulze ranking and the ranked pairs ranking are calculated and the winner is the top-ranked candidate of that of these two rankings that has the better Kemeny score. See:
- MKM-IG Charter
- Michael Kohlhase, MKM-IG Trustees Election Details & Ballot, November 2004
- Andrew A. Adams, MKM-IG Trustees Election 2005, December 2005
- Lionel Elie Mamane, Elections 2007: Ballot, August 2007
- ^ "Wahlmodus" (in (German)). Metalab.at. http://metalab.at/wiki/Generalversammlung_2007/Wahlmodus. Retrieved 2010-05-08.
- ^ Benjamin Mako Hill, Voting Machinery for the Masses, July 2008
- ^ See:
- Wahlen zum Neo-2-Freeze: Formalitäten, February 2010
- Hinweise zur Stimmabgabe, March 2010
- Ergebnisse, March 2010
- ^ See:
- ^ 2009 Director Elections
- ^ NSC Jersey election, NSC Jersey vote, September 2007
- ^ Online Voting Policy
- ^ 2010 OpenStack Community Election, November 2010
- ^ "Voting Procedures". Parkscholars.org. http://www.parkscholars.org/voting.php. Retrieved 2010-05-08.
- ^ National Congress 2011 Results, November 2011
- ^ §6(10) of the bylaws
- ^ §12.2.E of the statutory rules
- ^ 23 January 2011 meeting minutes
- ^ Piratenversammlung der Piratenpartei Schweiz, September 2010
- ^ 2006 Community for Pittsburgh Ultimate Board Election, September 2006
- ^ LogoVoting, December 2007
- ^ See:
- SPF Council Election Procedures
- 2006 SPF Council Election, January 2006
- 2007 SPF Council Election, January 2007
- ^ Squeak Oversight Board Election 2010, March 2010
- ^ See:
- Bylaws of the Students for Free Culture, article V, section 1.1.1
- Free Culture Student Board Elected Using Selectricity, February 2008
- ^ Election status update, September 2009
- ^ Minutes of the 2010 Annual Sverok Meeting, November 2010
- ^ See this mail.
- ^ See:
- Tornei:Carnevale 2007, March 2007
- Tornei:Sigle estate 2008, July 2008
- ^ See e.g. here (May 2009), here (August 2009), and here (December 2009).
- ^ See here and here.
- ^ See:
External links
General
- Schulze method website by Markus Schulze
Tutorials
- Schulze-Methode (German) by Christoph Giesel
- Condorcet Computations by Johannes Grabmeier
- Spieltheorie (German) by Bernhard Nebel
- Schulze-Methode (German) by the University of Stuttgart
Advocacy
- Descriptions of ranked-ballot voting methods by Rob LeGrand
- Accurate Democracy by Rob Loring
- Election Methods and Criteria by Kevin Venzke
- The Debian Voting System by Jochen Voss
- election-methods: a mailing list containing technical discussions about election methods
Books
- Christoph Börgers (2009), Mathematics of Social Choice: Voting, Compensation, and Division, SIAM, ISBN 0-89871-695-0
- Saul Stahl and Paul E. Johnson (2006), Understanding Modern Mathematics, Sudbury: Jones and Bartlett Publishers, ISBN 0-7637-3401-2
- Nicolaus Tideman (2006), Collective Decisions and Voting: The Potential for Public Choice, Burlington: Ashgate, ISBN 0-7546-4717-X
Software
- Modern Ballots and Python Vote Core by Brad Beattie
- Voting Software Project by Blake Cretney
- Condorcet with Dual Dropping Perl Scripts by Mathew Goldstein
- Condorcet Voting Calculator by Eric Gorr
- Selectricity and RubyVote by Benjamin Mako Hill [1] [2]
- Schulze voting for DokuWiki by Adrian Lang
- Electowidget by Rob Lanphier
- Online ranked-ballot voting calculator by Rob LeGrand
- Haskell Condorcet Module by Evan Martin
- Condorcet Internet Voting Service (CIVS) by Andrew Myers
- BetterPolls.com by Brian Olson
- OpenSTV by Jeffrey O'Neill
- LiquidFeedback
- preftools by the Public Software Group
- Voting Excel Template and Add-In
Legislative projects
Categories:- Debian
- Electoral reform
- Electoral systems
- Monotonic Condorcet methods
- Voting systems
- Proportional representation
Wikimedia Foundation. 2010.