Coombs' method

Part of the Politics series
Electoral methods
Single-winner
Simple majoritarianism Plurality  (First-past-the-post · Two-round · Exhaustive ballot) Preferential systems Condorcet methods  (Copeland's · Kemeny-Young · Minimax · Nanson's · Ranked pairs · Schulze) Bucklin voting Oklahoma primary electoral system Coombs' method Instant-runoff (alternative vote) Contingent vote Borda count Rated systems  (Range voting · Approval voting · Majority Judgment)
Multiple-winner
Proportional representation Party-list  (open · closed · mixed · local) Highest averages  (D'Hondt · Sainte-Laguë) Largest remainder  (Hare quota · Droop quota · Imperiali quota) Single transferable vote  (CPO-STV · Schulze STV · Wright system) Semi-proportional representation Cumulative voting Limited voting Single non-transferable vote Additional member system Parallel voting Majoritarian representation  (Plurality-at-large · Preferential block voting · General ticket)
Proxy voting
Random selection
Demarchy Sortition Random ballot
Social choice theory
Arrow's theorem Gibbard–Satterthwaite theorem Voting system criteria
Politics portal
v · d · e

The Coombs' method (or the Coombs rule)^[1] is a voting system created by Clyde Coombs used for single-winner elections in which each voter rank the candidates in order of preference. It is very similar to instant-runoff voting (also known as the alternative vote), a more common preferential voting system.

Procedures

Each voter rank-orders all of the candidates on their ballot. If at any time one candidate is ranked first (among non-eliminated candidates) by an absolute majority of the voters, then this is the winner. As long as this is not the case, the candidate which is ranked last (again among non-eliminated candidates) by the most (or a plurality of) voters is eliminated. Conversely, under instant run-off voting the candidate ranked first (among non-eliminated candidates) by the fewest voters is eliminated.

An example

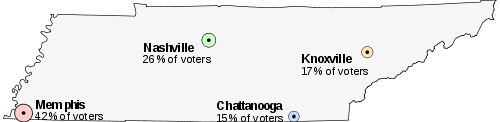
Imagine that Tennessee is having an election on the location of its capital. The population of Tennessee is concentrated around its four major cities, which are spread throughout the state. For this example, suppose that the entire electorate lives in these four cities, and that everyone wants to live as near to the capital as possible.

The candidates for the capital are:

• Memphis, the state's largest city, with 42% of the voters, but located far from the other cities
• Nashville, with 26% of the voters, near the center of Tennessee
• Knoxville, with 17% of the voters
• Chattanooga, with 15% of the voters

The preferences of the voters would be divided like this:

42% of voters (close to Memphis)	26% of voters (close to Nashville)	15% of voters (close to Chattanooga)	17% of voters (close to Knoxville)
Memphis Nashville Chattanooga Knoxville	Nashville Chattanooga Knoxville Memphis	Chattanooga Knoxville Nashville Memphis	Knoxville Chattanooga Nashville Memphis

Assuming all of the voters vote sincerely (strategic voting is discussed below), the results would be as follows, by percentage:

Coombs' method election results

City	Round 1		Round 2
	First	Last	First	Last
Memphis	42	58	42 0
Nashville	26	0	26 68
Chattanooga	15	0	15
Knoxville	17	42	17

• In the first round, no candidate has an absolute majority of first place votes (51).
• Memphis, having the most last place votes (26+15+17=58), is therefore eliminated.
• In the second round, Memphis is out of the running, and so must be factored out. Memphis was ranked first on Group A's ballots, so the second choice of Group A, Nashville, gets an additional 42 first place votes, giving it an absolute majority of first place votes (68 versus 15+17=32) thus making it the winner. Note that the last place votes are disregarded in the final round.

Use

The voting rounds used in Survivor (TV series) could be considered a variation of Coombs' method, with sequential voting rounds. Everyone votes for one candidate they support for elimination each round, and the candidate with a plurality of that vote is eliminated. A strategy difference is that sequential rounds of voting means the elimination choice is fixed in a ranked ballot Coombs' method, until that candidate is eliminated.

Potential for strategic voting

The Coombs' method is vulnerable to three strategies:^{[citation needed]} compromising, push-over and teaming.

See also

• List of democracy and elections-related topics

Notes

1. ^ Grofman, Bernard, and Scott L. Feld (2004) "If you like the alternative vote (a.k.a. the instant runoff), then you ought to know about the Coombs rule," Electoral Studies 23:641-59.