Majority Judgment

Part of the Politics series
Electoral methods
Single-winner
Simple majoritarianism Plurality First-past-the-post voting Multiple-round systems Two round Exhaustive ballot Preferential systems Condorcet methods Copeland's method Kemeny–Young method Minimax Nanson's method Ranked pairs Schulze method Bucklin voting Oklahoma primary electoral system Coombs' method Instant-runoff (alternative vote) Contingent vote Borda count Rated systems Range voting Approval voting Majority Judgment
Multiple-winner
Proportional representation Party-list  (open · closed · mixed · local) Highest averages D'Hondt method Sainte-Laguë method Largest remainder Hare quota Droop quota Imperiali quota Single transferable vote CPO-STV Schulze STV Wright system Semi-proportional representation Cumulative voting Limited voting Single non-transferable vote Additional member system Parallel voting Majoritarian representation Plurality-at-large Preferential block voting General ticket
Proxy voting
Delegable proxy Delegated proxy
Random selection
Demarchy Sortition Random ballot
Social choice theory
Arrow's theorem Gibbard–Satterthwaite theorem Voting system criteria
Politics portal
v · d · e

Majority Judgment is a single-winner voting system proposed by Michel Balinski and Rida Laraki. Voters freely grade each candidate in one of several named ranks, for instance from "excellent" to "bad", and the candidate with the highest median grade is the winner. If more than one candidate has the same median grade, a tiebreaker is used which sees the "closest-to-median" grade. Majority Judgment can be considered as a form of Bucklin voting which allows equal ranks.

Voting process

Voters are allowed rated ballots, on which they may assign a grade or judgment to each candidate. Badinski and Laraki suggest six grading levels, from "Excellent" to "Reject". Multiple candidates may be given the same grade if the voter desires.

The median grade for each candidate is found, for instance by sorting their list of grades and finding the middle one. If the middle falls between two different grades, the lower of the two is used.

The candidate with the highest median grade wins. If several candidates share the highest median grade, all other candidates are eliminated. Then, one copy of that grade is removed from each remaining candidate's list of grades, and the new median is found, until there is an unambiguous winner. For instance, if candidate X's sorted ratings were {"Good", "Good", "Fair", "Poor"}, while candidate Y had {"Excellent", "Fair", "Fair", "Fair"}, the rounded medians would both be "Fair". After removing one "Fair" from each list, the new lists are, respectively, {"Good", "Good", "Poor"} and {"Excellent", "Fair", "Fair"}, so X would win with a recalculated median of "Good".

Satisfied and failed criteria

Majority Judgment voting satisfies the majority criterion for rated ballots, the mutual majority criterion, the monotonicity criterion, and later-no-help. Assuming that ratings are given independently of other candidates, it satisfies the independence of clones criterion and the independence of irrelevant alternatives criterion^[1] - although this latter criterion is incompatible with the majority criterion if voters shift their judgments in order to express their preferences between the available candidates.

Majority judgement fails reversal symmetry, but this is only because of the rounding used. That is, a candidate whose ratings are {fair, fair} will beat a candidate whose ratings are {good, poor} in both directions, because the more variable rating will be rounded down. However, this failure only happens when a candidate's median is perfectly balanced between two scores, which is unlikely in proportion to the number of voters. The probability of this is negligible; it is only a constant factor higher than that of a perfect tie in a two way race, a situation in which any neutral system can fail to have reversal symmetry.

Majority Judgment voting fails the Condorcet criterion,^[2] later-no-harm,^[3] consistency,^[4] the Condorcet loser criterion,^[5] and the participation criterion.^[6] It also fails the ranked or preferential majority criterion, which is incompatible with the passed criterion independence of irrelevant alternatives.

Claimed resistance to tactical voting

In arguing for majority judgment, Balinski and Laraki (the system's inventors) mathematically proved that this system was the most "strategy-resistant" of any system which satisfies certain criteria they consider desirable. While the definition of "strategy-resistant" which they used for this proof is not generally shared, their overall case is bolstered by a study they did on simulated elections, in which, of the systems they studied, majority judgment least-often had its results swayed by strategic voters.

Example application

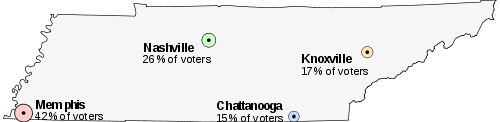
Imagine that Tennessee is having an election on the location of its capital. The population of Tennessee is concentrated around its four major cities, which are spread throughout the state. For this example, suppose that the entire electorate lives in these four cities, and that everyone wants to live as near to the capital as possible.

The candidates for the capital are:

• Memphis, the state's largest city, with 42% of the voters, but located far from the other cities
• Nashville, with 26% of the voters, near the center of Tennessee
• Knoxville, with 17% of the voters
• Chattanooga, with 15% of the voters

The preferences of the voters would be divided like this:

42% of voters (close to Memphis)	26% of voters (close to Nashville)	15% of voters (close to Chattanooga)	17% of voters (close to Knoxville)
Memphis Nashville Chattanooga Knoxville	Nashville Chattanooga Knoxville Memphis	Chattanooga Knoxville Nashville Memphis	Knoxville Chattanooga Nashville Memphis

If there were four ratings named "Excellent", "Good", "Fair", and "Poor", and each voter assigned four different ratings to the four cities, then the sorted scores would be as follows:

City	↓ Median point
Nashville
Chattanooga
Knoxville
Memphis
	Excellent      Good      Fair      Poor

The median rating for Nashville and Chatanooga is "Good"; for Knoxville, "Fair"; and for Memphis, "Poor". Nashville and Chatanooga are tied, so "Good" ratings have to be removed from both, until their medians become different. After removing 16% "Good" ratings from the votes of each, the sorted ratings are now:

City	↓ Median point
Nashville
Chattanooga
	Removed ratings (sorted to both ends evenly for easy comparison of medians with above).

Chatanooga now has the same number of "Fair" ratings as "Good" and "Excellent" combined, so its median is rounded down to "Fair", while Nashville's median remains at "Good"^[7] and so Nashville, the capital in real life, wins.

If voters from Knoxville and Chattanooga were to rate Nashville as "Poor" and/or both sets of voters were to rate Chattanooga as "Excellent", in an attempt to make their preferred candidate Chatanooga win, the winner would still be Nashville.

History

This system has several salient features, none of which is original in itself. First, it is a rated system. Since such systems include approval voting, which has been independently reinvented many times, this aspect is probably the least original. However, voting theory has tended to focus more on ranked systems, so this still distinguishes it from most voting system proposals. Second, it uses words, not numbers, to assign a commonly-understood meaning to each rating. Badinski and Laraki insist on the importance of the fact that ratings have a commonly-understood absolute meaning, and are not purely relative or strategic. Again, this aspect is unusual but not unheard-of throughout the history of voting. Finally, it uses the median to aggregate ratings. This method was explicitly proposed to assign budgets by Francis Galton in 1907^[8] and was implicitly used in Bucklin voting, a ranked or mixed ranked/rated system used soon thereafter in Progressive era reforms in the United States.

The full system of Majority Judgment was first proposed by Badinski and Laraki in 2007.^[9] That same year, they used it in an exit poll of French voters in the presidential election in the Bayrou area. Although this regional poll was not intended to be representative of the national result, it agreed with other local or national experiments in showing that Bayrou, rather than the eventual runoff winner Sarkozy, would have won under most alternative rules, including Majority Judgment. They also note that:

Everyone with some knowledge of French politics who was shown the results with the names of Sarkozy, Royal, Bayrou and Le Pen hidden invariably identified them: the grades contain meaningful information.^[10]

It has since been used in judging wine competitions and in other political research polling in France and the US.^[11]

See also

• Approval voting
• Range voting
• Voting system
• List of democracy and elections-related topics

Notes

1. ^ Badinski and Laraki, Majority Judgment, p. 217
2. ^ Strategically in the strong Nash equilibrium, MJ passes the Condorcet criterion.
3. ^ MJ provides a weaker guarantee similar to LNH: rating another candidate at or below your preferred winner's median rating (as opposed to your own rating for the winner) cannot harm the winner.
4. ^ Majority judgment's inventors argue that meaning should be assigned to the absolute rating that the system assigns to a candidate; that if one electorate rates candidate X as "excellent" and Y as "good", while another one ranks X as "fair" and Y as "poor", these two electorates do not in fact agree. Therefore, they define a criterion they call "rating consistency", which Majority Judgment passes. Badinski and Laraki, "Judge, don't Vote", November 2010
5. ^ Nevertheless, it passes a slightly weakened version, the majority condorcet loser criterion, in which all defeats are by an absolute majority (for instance, if there aren't equal rankings).
6. ^ It can only fail the participation criterion when, among other conditions, the new ballot rates both of the candidates in question on the same side of the winning median, and the prior distribution of ratings is more sharply-peaked or irregular for one of the candidates.
7. ^ After removal, Chatanooga has 42% of the initial electorate at "Fair", 27% "Good", and 15% "Excellent", while Nashville has 32% "Fair", 26% "Good", and 26% "Excellent"
8. ^ Francis Galton, “One vote, one value,” Letter to the editor, Nature vol. 75, Feb. 28, 1907, p. 414.
9. ^ Balinski M. and R. Laraki (2007) «A theory of measuring, electing and ranking». Proceedings of the National Academy of Sciences USA, vol. 104, no. 21, 8720-8725.
10. ^ Balinski M. and R. Laraki (2007) «Election by Majority Judgement: Experimental Evidence». Cahier du Laboratoire d’Econométrie de l’Ecole Polytechnique 2007-28. Chapter in the book: «In Situ and Laboratory Experiments on Electoral Law Reform: French Presidential Elections», Edited by Bernard Dolez, Bernard Grofman and Annie Laurent. Springer, to appear in 2011.
11. ^ Balinski M. and R. Laraki (2010) «Judge: Don't vote». Cahier du Laboratoire d’Econométrie de l’Ecole Polytechnique 2010-27.

References

• Balinski, Michel, and Laraki, Rida (2010). Majority Judgment: Measuring, Ranking, and Electing, MIT Press