Pushout (category theory)

In category theory, a branch of mathematics, a pushout (also called a fibered coproduct or fibered sum or cocartesian square or amalgamed sum) is the colimit of a diagram consisting of two morphisms f : Z → X and g : Z → Y with a common domain: it is the colimit of the span $X \leftarrow Z \rightarrow Y$.

The pushout is the categorical dual of the pullback.

Universal property

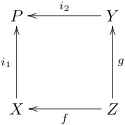
Explicitly, the pushout of the morphisms f and g consists of an object P and two morphisms i₁ : X → P and i₂ : Y → P for which the following diagram commutes:

Moreover, the pushout (P, i₁, i₂) must be universal with respect to this diagram. That is, for any other such set (Q, j₁, j₂) for which the following diagram commutes, there must exist a unique u : P → Q also making the diagram commute:

As with all universal constructions, the pushout, if it exists, is unique up to a unique isomorphism.

Examples of pushouts

Here are some examples of pushouts in familiar categories. Note that in each case, we are only providing a construction of an object in the isomorphism class of pushouts; as mentioned above, there may be other ways to construct it, but they are all equivalent.

1. Suppose that X and Y as above are sets. Then if we write Z for their intersection, there are morphisms f : Z → X and g : Z → Y given by inclusion. The pushout of f and g is the union of X and Y together with the inclusion morphisms from X and Y.

2. The construction of adjunction spaces is an example of pushouts in the category of topological spaces. More precisely, if Z is a subspace of Y and g : Z → Y is the inclusion map we can "glue" Y to another space X along Z using an "attaching map" f : Z → X. The result is the adjunction space $X \cup_{f} Y$ which is just the pushout of f and g. More generally, all identification spaces may be regarded as pushouts in this way.

3. A special case of the above is the wedge sum or one-point union; here we take X and Y to be pointed spaces and Z the one-point space. Then the pushout is $X \vee Y$, the space obtained by gluing the basepoint of X to the basepoint of Y.

4. In the category of abelian groups, pushouts can be thought of as "direct sum with gluing" in the same way we think of adjunction spaces as "disjoint union with gluing". The zero group is a subgroup of every group, so for any abelian groups A and B, we have homomorphisms

f : 0 → A

and

g : 0 → B.

The pushout of these maps is the direct sum of A and B. Generalizing to the case where f and g are arbitrary homomorphisms from a common domain Z, one obtains for the pushout a quotient group of the direct sum; namely, we mod out by the subgroup consisting of pairs (f(z),-g(z)). Thus we have "glued" along the images of Z under f and g. A similar trick yields the pushout in the category of R-modules for any ring R.

5. In the category of groups, the pushout is called the free product with amalgamation. It shows up in the Seifert-van Kampen theorem of algebraic topology (see below).

Properties

• Whenever A∪_CB and B∪_CA exist, there is an isomorphism A∪_CB ≅ B∪_CA.
• Whenever the pushout A∪_AB exists, there is an isomorphism B ≅ A∪_AB (this follows from the universal property of the pushout).

Construction via coproducts and coequalizers

Pushouts are equivalent to coproducts, and coequalizers (if there is an initial object) in the sense that:

• Coproducts are a pushout from the initial object, and the coequalizer of f, g : X → Y is the pushout of [f, g] and [1_X, 1_X], so if there are pushouts (and an initial object), then there are coequalizers and coproducts;
• Pushouts can be constructed from coproducts and coequalizers, as described below (the pushout is the coequalizer of the maps to the coproduct).

All of the above examples may be regarded as special cases of the following very general construction, which works in any category C satisfying:

• For any objects A and B of C, their coproduct exists in C;
• For any morphisms j and k of C with the same domain and target, the coequalizer of j and k exists in C.

In this setup, we obtain the pushout of morphisms f : Z → X and g : Z → Y by first forming the coproduct of the targets X and Y. We then have two morphisms from Z to this coproduct. We can either go from Z to X via f, then include into the coproduct, or we can go from Z to Y via g, then include. The pushout of f and g is the coequalizer of these new maps.

Application: The Seifert-van Kampen theorem

Returning to topology, the Seifert-van Kampen theorem answers the following question. Suppose we have a path-connected space X, covered by path-connected open subspaces A and B whose intersection is also path-connected. (Assume also that the basepoint * lies in the intersection of A and B.) If we know the fundamental groups of A, B, and their intersection D, can we recover the fundamental group of X? The answer is yes, provided we also know the induced homomorphisms $\pi_1(D,*) \to \pi_1(A,*)$ and $\pi_1(D,*) \to \pi_1(B,*).$ The theorem then says that the fundamental group of X is the pushout of these two induced maps. Of course, X is the pushout of the two inclusion maps of D into A and B. Thus we may interpret the theorem as confirming that the fundamental group functor preserves pushouts of inclusions. We might expect this to be simplest when D is simply connected, since then both homomorphisms above have trivial domain. Indeed this is the case, since then the pushout (of groups) reduces to the free product, which is the coproduct in the category of groups. In a most general case we will be speaking of a free product with amalgamation.

There is a detailed exposition of this, in a slightly more general setting (covering groupoids) in the book by J. P. May listed in the references.

References

• May, J. P. A concise course in algebraic topology. University of Chicago Press, 1999.

  An introduction to categorical approaches to algebraic topology: the focus is on the algebra, and assumes a topological background.

External links

• Interactive Web page which generates examples of pushouts in the category of finite sets. Written by Jocelyn Paine.