- Intersection (set theory)
-
 Intersections of the Greek, Latin and Russian alphabet (upper case graphemes)
Intersections of the Greek, Latin and Russian alphabet (upper case graphemes)
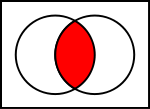
(The intersection of Greek and Latin letters is used for the Greek licence plates.)In mathematics, the intersection (denoted as ∩) of two sets A and B is the set that contains all elements of A that also belong to B (or equivalently, all elements of B that also belong to A), but no other elements.[1]
For explanation of the symbols used in this article, refer to the table of mathematical symbols.
Contents
Basic definition
The intersection of A and B is written "A ∩ B". Formally:
- x ∈ A ∩ B if and only if
- x ∈ A and
- x ∈ B.
- For example:
- The intersection of the sets {1, 2, 3} and {2, 3, 4} is {2, 3}.
- The number 9 is not in the intersection of the set of prime numbers {2, 3, 5, 7, 11, …} and the set of odd numbers {1, 3, 5, 7, 9, 11, …}.
If the intersection of two sets A and B is empty, that is they have no elements in common, then they are said to be disjoint, denoted: A ∩ B = ∅. For example the sets {1, 2} and {3, 4} are disjoint, written
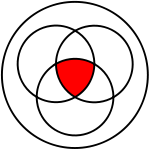
{1, 2} ∩ {3, 4} = ∅.More generally, one can take the intersection of several sets at once. The intersection of A, B, C, and D, for example, is A ∩ B ∩ C ∩ D = A ∩ (B ∩ (C ∩ D)). Intersection is an associative operation; thus,
A ∩ (B ∩ C) = (A ∩ B) ∩ C.If the sets A and B are closed under complement then the intersection of A and B may be written as the complement of the union of their complements, derived easily from De Morgan's laws:
A ∩ B = (Ac ∪ Bc)cArbitrary intersections
The most general notion is the intersection of an arbitrary nonempty collection of sets. If M is a nonempty set whose elements are themselves sets, then x is an element of the intersection of M if and only if for every element A of M, x is an element of A. In symbols:
The notation for this last concept can vary considerably. Set theorists will sometimes write "⋂M", while others will instead write "⋂A∈M A". The latter notation can be generalized to "⋂i∈I Ai", which refers to the intersection of the collection {Ai : i ∈ I}. Here I is a nonempty set, and Ai is a set for every i in I.
In the case that the index set I is the set of natural numbers, notation analogous to that of an infinite series may be seen:
When formatting is difficult, this can also be written "A1 ∩ A2 ∩ A3 ∩ ...", even though strictly speaking, A1 ∩ (A2 ∩ (A3 ∩ ... makes no sense. (This last example, an intersection of countably many sets, is actually very common; for an example see the article on σ-algebras.)
Finally, let us note that whenever the symbol "∩" is placed before other symbols instead of between them, it should be of a larger size (⋂).
Nullary intersection
 Conjunctions of the arguments in parentheses
Conjunctions of the arguments in parentheses
The conjunction of no argument is the tautology (compare: empty product); accordingly the intersection of no set is the universe.Note that in the previous section we excluded the case where M was the empty set (∅). The reason is as follows: The intersection of the collection M is defined as the set (see set-builder notation)
If M is empty there are no sets A in M, so the question becomes "which x's satisfy the stated condition?" The answer seems to be every possible x. When M is empty the condition given above is an example of a vacuous truth. So the intersection of the empty family should be the universal set, which according to standard (ZFC) set theory, does not exist.
A partial fix for this problem can be found if we agree to restrict our attention to subsets of a fixed set U called the universe. In this case the intersection of a family of subsets of U can be defined as
Now if M is empty there is no problem. The intersection is just the entire universe U, which is a well-defined set by assumption.
References
See also
Categories:- Abstract algebra
- Algebra
- Basic concepts in set theory
- Binary operations
- x ∈ A ∩ B if and only if
Wikimedia Foundation. 2010.