- Symmetric difference
-
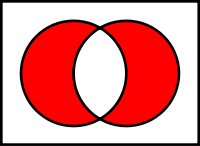
Venn diagram of 
The symmetric difference is
the union without the intersection:



In mathematics, the symmetric difference of two sets is the set of elements which are in either of the sets and not in their intersection. The symmetric difference of the sets A and B is commonly denoted by
or
For example, the symmetric difference of the sets {1,2,3} and {3,4} is {1,2,4}. The symmetric difference of the set of all students and the set of all females consists of all male students together with all female non-students.
The power set of any set becomes an abelian group under the operation of symmetric difference, with the empty set as the neutral element of the group and every element in this group being its own inverse. The power set of any set becomes a Boolean ring with symmetric difference as the addition of the ring and intersection as the multiplication of the ring.
Contents
Properties
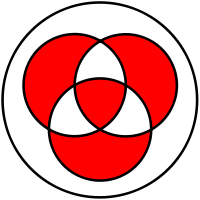
Venn diagram of 
The symmetric difference is equivalent to the union of both relative complements, that is:
and it can also be expressed as the union of the two sets, minus their intersection:
or with the XOR operation:
The symmetric difference is commutative and associative:
Thus, the repeated symmetric difference is an operation on a multiset of sets giving the set of elements which are in an odd number of sets.
The symmetric difference of two repeated symmetric differences is the repeated symmetric difference of the join of the two multisets, where for each double set both can be removed. In particular:
This implies a sort of triangle inequality: the symmetric difference of A and C is contained in the union of the symmetric difference of A and B and that of B and C. (But note that for the diameter of the symmetric difference the triangle inequality does not hold.)
The empty set is neutral, and every set is its own inverse:
Taken together, we see that the power set of any set X becomes an abelian group if we use the symmetric difference as operation. Because every element in this group is its own inverse, this is in fact a vector space over the field with 2 elements Z2. If X is finite, then the singletons form a basis of this vector space, and its dimension is therefore equal to the number of elements of X. This construction is used in graph theory, to define the cycle space of a graph.
Intersection distributes over symmetric difference:
and this shows that the power set of X becomes a ring with symmetric difference as addition and intersection as multiplication. This is the prototypical example of a Boolean ring.
The symmetric difference can be defined in any Boolean algebra, by writing
This operation has the same properties as the symmetric difference of sets.
n-ary symmetric difference
As above, the symmetric difference of a collection of sets contains just elements which are in an odd number of the sets in the collection:
 .
.
Evidently, this is well-defined only when each element of the union
 is contributed by a finite number of elements of M.
is contributed by a finite number of elements of M.Symmetric difference on measure spaces
As long as there is a notion of "how big" a set is, the symmetric difference between two sets can be considered a measure of how "far apart" they are. Formally, if μ is a σ-finite measure defined on a σ-algebra Σ, the function,
is a pseudometric on Σ. d becomes a metric if Σ is considered modulo the equivalence relation X ~ Y if and only if
 . The resulting metric space is separable if and only if L2(μ) is separable.
. The resulting metric space is separable if and only if L2(μ) is separable.See also
- Algebra of sets
- Boolean function
- Difference (set theory)
- Exclusive or
- Fuzzy set
- Logical graph
- Minimal negation operator
- Set theory
- Symmetry
References
Categories:- Algebra
- Basic concepts in set theory
- Binary operations
Wikimedia Foundation. 2010.













