Compound interest

The effect of earning 20% annual interest on an initial $1,000 investment at various compounding frequencies

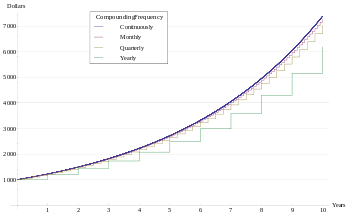
Compound interest arises when interest is added to the principal, so that from that moment on, the interest that has been added also itself earns interest. This addition of interest to the principal is called compounding. A bank account, for example, may have its interest compounded every year: in this case, an account with $1000 initial principal and 20% interest per year would have a balance of $1200 at the end of the first year, $1440 at the end of the second year, and so on.

In order to define an interest rate fully, and enable one to compare it with other interest rates, the interest rate and the compounding frequency must be disclosed. Since most people prefer to think of rates as a yearly percentage, many governments require financial institutions to disclose the equivalent yearly compounded interest rate on deposits or advances. For instance, the yearly rate for a loan with 1% interest per month is approximately 12.68% per annum (1.01¹² − 1). This equivalent yearly rate may be referred to as annual percentage rate (APR), annual equivalent rate (AER), annual percentage yield, effective interest rate, effective annual rate, and by other terms. When a fee is charged up front to obtain a loan, APR usually counts that cost as well as the compound interest in converting to the equivalent rate. These government requirements assist consumers to compare the actual costs of borrowing more easily.

For any given interest rate and compounding frequency, an "equivalent" rate for any different compounding frequency exists.

Compound interest may be contrasted with simple interest, where interest is not added to the principal (there is no compounding). Compound interest is standard in finance and economics, and simple interest is used infrequently (although certain financial products may contain elements of simple interest).

Terminology

The effect of compounding depends on the frequency with which interest is compounded and the periodic interest rate which is applied. Therefore, in order to define accurately the amount to be paid under a legal contract with interest, the frequency of compounding (yearly, half-yearly, quarterly, monthly, daily, etc.) and the interest rate must be specified. Different conventions may be used from country to country, but in finance and economics the following usages are common:

Periodic rate: the interest that is charged (and subsequently compounded) for each period, divided by the amount of the principal. The periodic rate is used primarily for calculations, and is rarely used for comparison. The nominal annual rate or nominal interest rate is defined as the periodic rate multiplied by the number of compounding periods per year. For example, a monthly rate of 1% is equivalent to an annual nominal interest of 12%.

Effective annual rate: this reflects the effective rate as if annual compounding were applied: in other words it is the total accumulated interest that would be payable up to the end of one year, divided by the principal.

Economists generally prefer to use effective annual rates to allow for comparability. In finance and commerce, the nominal annual rate may however be the one quoted instead. When quoted together with the compounding frequency, a loan with a given nominal annual rate is fully specified (the effect of interest for a given loan scenario can be precisely determined), but the nominal rate cannot be directly compared with loans that have a different compounding frequency.

Loans and finance may have other "non-interest" charges, and the terms above do not attempt to capture these differences. Other terms such as annual percentage rate and annual percentage yield may have specific legal definitions and may or may not be comparable, depending on the jurisdiction.

The use of the terms above (and other similar terms) may be inconsistent, and vary according to local custom or marketing demands, for simplicity or for other reasons.

Exceptions

• US and Canadian T-Bills (short term Government debt) have a different convention. Their interest is calculated as (100 − P)/Pbnm, where P is the price paid. Instead of normalizing it to a year, the interest is prorated by the number of days t: (365/t)×100. (See day count convention).
• The interest on corporate bonds and government bonds is usually payable twice yearly. The amount of interest paid (each six months) is the disclosed interest rate divided by two (multiplied by the principal). The yearly compounded rate is higher than the disclosed rate.
• Canadian mortgage loans are generally semi-annual compounding with monthly (or more frequent) payments.^[1]
• U.S. mortgages use an amortizing loan, not compound interest. With these loans, an amortization schedule is used to determine how to apply payments toward principal and interest. Interest generated on these loans is not added to the principal, but rather is paid off monthly as the payments are applied.
• It is sometimes mathematically simpler, e.g. in the valuation of derivatives to use continuous compounding, which is the limit as the compounding period approaches zero. Continuous compounding in pricing these instruments is a natural consequence of Itō calculus, where derivatives are valued at ever increasing frequency, until the limit is approached and the derivative is valued in continuous time.

Mathematics of interest rates

Simplified calculation

Formulae are presented in greater detail at time value of money.

In the formula below, i is the effective interest rate per period. FV and PV represent the future and present value of a sum. n represents the number of periods.

These are the most basic formulas:

$FV = PV ( 1+i )^n\,$

The above calculates the future value (FV) of an investment's present value (PV) accruing at a fixed interest rate (i) for n periods.

$PV = \frac {FV} {\left( 1+i \right)^n}\,$

The above calculates what present value (PV) would be needed to produce a certain future value (FV) if interest (i) accrues for n periods.

$i = \left( \frac {FV} {PV} \right)^\frac {1} {n}- 1$

The above calculates the compound interest rate achieved if an initial investment of PV returns a value of FV after n accrual periods.

$n = \frac {\log(FV) - \log(PV)} {\log(1 + i)}$

The above formula calculates the number of periods required to get FV given the PV and the interest rate (i). The log function can be in any base, e.g. natural log (ln), as long as consistent bases are used all throughout calculation.

Compound

A formula for calculating annual compound interest is

$A = P \left(1 + \frac{r}{n}\right)^{nt}$

Where,

• A = final amount
• P = principal amount (initial investment)
• r = annual nominal interest rate (as a decimal)

(it should not be in percentage)

• n = number of times the interest is compounded per year
• t = number of years

Example usage: An amount of $1500.00 is deposited in a bank paying an annual interest rate of 4.3%, compounded quarterly. Find the balance after 6 years.

A. Using the formula above, with P = 1500, r = 4.3/100 = 0.043, n = 4, and t = 6:

$A=1500\left(1 + \frac{0.043}{4}\right)^{4 \times 6} =1938.84$

So, the balance after 6 years is approximately $1,938.84.

Periodic compounding

The amount function for compound interest is an exponential function in terms of time.

$A(t) = A_0 \left(1 + \frac {r} {n}\right) ^ {nt}$

• t = Total time in years

• n = Number of compounding periods per year (note that the total number of compounding periods is $n \cdot t$)

• r = Nominal annual interest rate expressed as a decimal. e.g.: 6% = 0.06

As n increases, the rate approaches an upper limit of e^r − 1. This rate is called continuous compounding, see below.

Since the principal A(0) is simply a coefficient, it is often dropped for simplicity, and the resulting accumulation function is used in interest theory instead. Accumulation functions for simple and compound interest are listed below:

$a(t)=1+t r\,$

$a(t) = \left(1 + \frac {r} {n}\right) ^ {nt}$

Note: A(t) is the amount function and a(t) is the accumulation function.

Continuous compounding

Continuous compounding can be thought of as making the compounding period infinitesimally small; therefore achieved by taking the limit of n to infinity. One should consult definitions of the exponential function for the mathematical proof of this limit.

P₁ = P₀e^rt take t as 1 so

ln(P₁ / P₀) = r = ln(1 + R)

where R is simple return and r is called log return because it is the logarithm of normal return.

$a(t)=\lim_{n\to\infty}\left(1+\frac{r}{n}\right)^{nt}$

a(t) = e^rt

The amount function is simply

A(t) = A₀e^rt

The interest rate expressed as a continuously compounded rate is called the force of interest. The annual force of interest is simply 12 times the monthly force of interest.

The effective interest rate per year is

i = e^r − 1

Using this i the amount function can be written as:

A(t) = A₀(1 + i)^t

or

A = P(1 + i)^t

See also logarithmic or continuously compounded return.

Force of interest

Part of a series of articles on The mathematical constant e Natural logarithm · Exponential function Applications in: compound interest · Euler's identity & Euler's formula  · half-lives & exponential growth/decay Defining e: proof that e is irrational  · representations of e · Lindemann–Weierstrass theorem People John Napier  · Leonhard Euler Schanuel's conjecture

In mathematics, the accumulation functions are often expressed in terms of e, the base of the natural logarithm. This facilitates the use of calculus methods in manipulation of interest formulae.

For any continuously differentiable accumulation function a(t) the force of interest, or more generally the logarithmic or continuously compounded return is a function of time defined as follows:

$\delta_{t}=\frac{a'(t)}{a(t)}\,$

which is the rate of change with time of the natural logarithm of the accumulation function.

Conversely:

$a(n)=e^{\int_0^n \delta_t\, dt}\ ,$ (since a(0) = 1)

When the above formula is written in differential equation format, the force of interest is simply the coefficient of amount of change.

$da(t)=\delta_{t}a(t)\,dt\,$

For compound interest with a constant annual interest rate r the force of interest is a constant, and the accumulation function of compounding interest in terms of force of interest is a simple power of e:

$\delta=\ln(1+r)\,$

$a(t)=e^{t\delta}\,$

The force of interest is less than the annual effective interest rate, but more than the annual effective discount rate. It is the reciprocal of the e-folding time. See also notation of interest rates.

Compounding basis

See Day count convention

To convert an interest rate from one compounding basis to another compounding basis, the following formula applies:

$r_2=\left[\left(1+\frac{r_1}{n_1}\right)^\frac{n_1}{n_2}-1\right]n_2$

where r₁ is the stated interest rate with compounding frequency n₁ and r₂ is the stated interest rate with compounding frequency n₂.

When interest is continuously compounded:

$R=n\ln{\left(1+r/n\right)}$

where R is the interest rate on a continuous compounding basis and r is the stated interest rate with a compounding frequency n.

Monthly mortgage payments

The interest on mortgages is often compounded monthly. The formula for payments is found from the following argument.

Notation

I = Note percentage rate

i = Monthly percentage rate = I/12 (so that the APR = (1+i)^12 - 1)

T = Term in years

Y= I•T

X = ½ I•T = ½ Y

n = 12•T = term in months

L = Principal or amount of loan

P = monthly payment

Exact formula for P

If the term were only one month then clearly

(1 + i)L = P so that $L = \frac{P}{1+i}$. If the term were two months then (1 + i)((1 + i)L − P) = P so that $L = \frac{P}{1+i}+\frac{P}{(1+i)^2}$. For a term of n months then $L = P \sum_{j=1}^n \frac{1}{(1+i)^j}$.

This can be simplified by noting that $(1+i)L = P \sum_{j=0}^{n-1} \frac{1}{(1+i)^j}$ and taking the difference: $(1+i)L-L=iL=P\left(1-\frac{1}{(1+i)^n}\right)$ so that

$P= \frac{Li}{1-\frac{1}{(1+i)^n}}=\frac{Li}{1-e^{-n\ln(1+i)}}$

This formula for the monthly payment on a U.S. mortgage is exact and is what banks use.

Approximate formula for P

A formula that is accurate to within a few percent can be found by noting that for typical U.S. note rates (I < 8% and terms T=10-30 years), the monthly note rate is small compared to 1: i < < 1 so that the $ln(1+i)\approx i$ which yields a simplification so that $P\approx \frac{Li}{1-e^{-ni}}= \frac{L}{n}\frac{ni}{1-e^{-ni}}$

which suggests defining auxiliary variables

$Y\equiv n i = TI$

$P_0\equiv \frac{L}{n}$.

P₀ is the monthly payment required for a zero interest loan paid off in n installments. In terms of these variables the approximation can be written

$P\approx P_0 \frac{Y}{1-e^{-Y}}$

The function $f(Y)\equiv \frac{Y}{1-e^{-Y}}-\frac{Y}{2}$ is even: f(Y) = f( − Y) implying that it can be expanded in even powers of Y.

It follows immediately that $\frac{Y}{1-e^{-Y}}$ can be expanded in even powers of Y plus the single term: Y / 2

It will prove convenient then to define

$X=\frac{1}{2}Y = \frac{1}{2}IT$

so that $P\approx P_0 \frac{2X}{1-e^{-2X}}$ which can be expanded: $P\approx P_0 \left(1 + X + \frac{X^2}{3} - \frac{1}{45} X^4 + ...\right)$

where the ellipses indicate terms that are higher order in even powers of X. The expansion

$P\approx P_0 \left(1 + X + \frac{X^2}{3}\right)$

is valid to better than 1% provided $X\le 1$.

Example

For a mortgage with a term of 30 years and a note rate of 4.5% we find:

T = 30

I = .045

$X=\frac{1}{2}IT =\frac{1}{2} \times .045 \times 30 = .675$

which suggests that the approximation

$P\approx P_0 \left(1 + X + \frac{1}{3}X^2\right)$ is accurate to better than one percent for typical U.S. mortgage terms in January 2009. The formula becomes less accurate for higher rates and longer terms.

For a 30-year term on a loan of $120,000 and a 4.5% note rate we find:

L = 120000

$P_0=\frac{$120,000}{360}=$333.33$

so that

$P\approx P_0 \left(1 + X + \frac{1}{3}X^2 \right)=$333.33 (1+.675+.675^2/3)=$608.96$

The exact payment amount is P = $608.02 so the approximation is an overestimate of about a sixth of a percent.

Other approximations

The approximate formula $P\approx P_0 \frac{Y}{1-e^{-Y}}$ yields $P_0\approx $607.47$ which is a slight underestimate of the exact result. This underestimate results from the approximation $\ln(1+i)\approx i$. Keeping the next correction in the expansion of $\ln(1+i)\approx i-i^2/2+\ldots$ results in an approximate formula $P\approx P_0 \frac{Y}{1-e^{-Y}e^{iY/2}}=$608.018$ which is off by two tenths of a cent. The simplest approximation discussed

$P\approx P_0 \left(1 + X + \frac{1}{3}X^2\right)$

is good to within better than a percent for typical US mortgages in early 2009. The approximation $P\approx P_0 (1 + X )$ is an underestimate of around 10% for such mortgage payments.

History

Compound interest was once regarded as the worst kind of usury, and was severely condemned by Roman law, as well as the common laws of many other countries. ^[2]

Richard Witt's book Arithmeticall Questions, published in 1613, was a landmark in the history of compound interest. It was wholly devoted to the subject (previously called anatocism), whereas previous writers had usually treated compound interest briefly in just one chapter in a mathematical textbook. Witt's book gave tables based on 10% (the then maximum rate of interest allowable on loans) and on other rates for different purposes, such as the valuation of property leases. Witt was a London mathematical practitioner and his book is notable for its clarity of expression, depth of insight and accuracy of calculation, with 124 worked examples.^[3][4]

The Qur'an explicitly mentions compound interest as a great sin. Usury (oppressive interest), known in Arabic as "riba", is considered wrong:

“	O ye who believe! Devour not usury, doubling and quadrupling (the sum lent). Observe your duty to Allah, that ye may be successful.	”
	— Quran 3:130

In one passage, the Bible addresses the charging of interest in the following manner:

“	Take no usury or interest from him; but fear your God, that your brother may live with you. You shall not lend him your money for usury, nor lend him your food at a profit.	”
	— Leviticus 25:36-37

See also

• Effective interest rate
• Nominal interest rate
• Exponential growth
• Rate of return on investment
• Credit card interest
• Fisher equation
• Simple Interest
• Yield curve
• Amortizing loan

References

1. ^ http://laws.justice.gc.ca/en/showdoc/cs/I-15/bo-ga:s_6//en#anchorbo-ga:s_6 Interest Act (Canada), Department of Justice. The Interest Act specifies that interest is not recoverable unless the mortgage loan contains a statement showing the rate of interest chargeable, "calculated yearly or half-yearly, not in advance." In practice, banks use the half-yearly rate.
2. ^  This article incorporates content from the 1728 Cyclopaedia, a publication in the public domain.
3. ^ Lewin, C G (1970). "An Early Book on Compound Interest - Richard Witt's Arithmeticall Questions". Journal of the Institute of Actuaries 96 (1): 121–132. 
4. ^ Lewin, C G (1981). "Compound Interest in the Seventeenth Century". Journal of the Institute of Actuaries 108 (3): 423–442.