Letter frequency

Letter frequency

The frequency of letters in text has often been studied for use in cryptography, and frequency analysis in particular. No exact letter frequency distribution underlies a given language, since all writers write slightly differently. Linotype machines sorted the letters' frequencies as etaoin shrdlu cmfwyp vbgkqj xz based on the experience and custom of manual compositors. Likewise, Modern International Morse code encodes the most frequent letters with the shortest symbols; arranging the Morse alphabet into groups of letters that require equal amounts of time to transmit, and then sorting these groups in increasing order, yields e it san hurdm wgvlfbk opjxcz yq. Similar ideas are used in modern data-compression techniques such as Huffman coding.

More recent analyses show that letter frequencies, like word frequencies, tend to vary, both by writer and by subject. One cannot write an essay about x-rays without using frequent Xs, and the essay will have an especially strange letter frequency if the essay is about the frequent use of x-rays to treat zebras in Qatar. Different authors have habits which can be reflected in their use of letters. Hemingway's writing style, for example, is visibly different from Faulkner's. Letter, bigram, trigram, word frequencies, word length, and sentence length can be calculated for specific authors, and used to prove or disprove authorship of texts, even for authors whose styles aren't so divergent.

Accurate average letter frequencies can only be gleaned by analyzing a large amount of representative text. With the availability of modern computing and collections of large text corpora, such calculations are easily made. This Deafandblind link details examples from a variety of sources, (press reporting, religious text, scientific text and general fiction) and there are differences especially for general fiction with the position of 'h' and 'i'. The example differs from the linotype 'etaoin shrdlu' to come out as 'etaoHn Isrdlu'. There is an unproven statement[by whom?] that conversation is similar in frequency to general fiction.

Herbert S. Zim, in his classic introductory cryptography text "Codes and Secret Writing", gives the English letter frequency sequence as "ETAON RISHD LFCMU GYPWB VKXJQ Z", the most common letter pairs as "TH HE AN RE ER IN ON AT ND ST ES EN OF TE ED OR TI HI AS TO", and the most common doubled letters as "LL EE SS OO TT FF RR NN PP CC".[1]

The 'top twelve' letters comprise about 80% of the total usage. The 'top eight" letters comprise about 65% of the total usage. A spy using the VIC cipher or some other cipher based on a straddling checkerboard typically uses a mnemonic such as "a sin to err" (dropping the second "r") to remember the top 8 characters.

The use of letter frequencies and frequency analysis plays a fundamental role in cryptograms and several word puzzle games, including Hangman, Scrabble, Bananagrams, and the television game show Wheel of Fortune.

Letter frequencies had a strong effect on the design of some keyboard layouts. The most-frequent letters are on the bottom row of the Blickensderfer typewriter. The most-frequent letters are on the home row of the Dvorak Simplified Keyboard.

Contents

Relative frequencies of letters in the English language

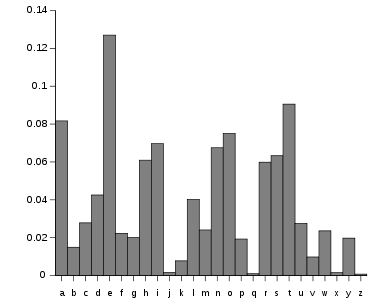
Relative frequencies of letters in text.
Relative frequencies ordered by frequency.

The letter frequencies for English are listed below.[2] However, this table differs slightly from others, such as Cornell University Math Explorer's Project, which produced this table after measuring 40,000 words.

Letter Frequency
a 8.167%
b 1.492%
c 2.782%
d 4.253%
e 12.702%
f 2.228%
g 2.015%
h 6.094%
i 6.966%
j 0.153%
k 0.772%
l 4.025%
m 2.406%
n 6.749%
o 7.507%
p 1.929%
q 0.095%
r 5.987%
s 6.327%
t 9.056%
u 2.758%
v 0.978%
w 2.360%
x 0.150%
y 1.974%
z 0.074%


In English, the space is slightly more frequent than the top letter (7% more frequent than, or 107% as frequent as, e),[citation needed] and the non-alphabetic characters (digits, punctuation, etc.) occupy the fourth position, between t and a.[3]

Relative frequencies of the first letters of a word in the English language

First Letter of a word frequencies:[4]

Letter Frequency
a 11.602%
b 4.702%
c 3.511%
d 2.670%
e 2.000%
f 3.779%
g 1.950%
h 7.232%
i 6.286%
j 0.631%
k 0.690%
l 2.705%
m 4.374%
n 2.365%
o 6.264%
p 2.545%
q 0.173%
r 1.653%
s 7.755%
t 16.671%
u 1.487%
v 0.619%
w 6.661%
x 0.005%
y 1.620%
z 0.050%

Relative frequencies of letters in other languages

Letter French [5] German [6] Spanish [7] Portuguese [8] Esperanto [9] Italian[10] Turkish Swedish[11] Polish[12] Dutch [13]
a 7.636% 6.51% 12.53% 14.63% 12.12% 11.74% 11.68% 9.3% 8.0% 7.49%
b 0.901% 1.89% 1.42% 1.04% 0.98% 0.92% 2.95% 1.3% 1.3% 1.58%
c 3.260% 3.06% 4.68% 3.88% 0.78% 4.5% 0.97% 1.3% 3.8% 1.24%
d 3.669% 5.08% 5.86% 4.99% 3.04% 3.73% 4.87% 4.5% 3.0% 5.93%
e 14.715% 17.40% 13.68% 12.57% 8.99% 11.79% 9.01% 9.9% 6.9% 18.91%
f 1.066% 1.66% 0.69% 1.02% 1.03% 0.95% 0.44% 2.0% 0.1% 0.81%
g 0.866% 3.01% 1.01% 1.30% 1.17% 1.64% 1.34% 3.3% 1.0% 3.40%
h 0.737% 4.76% 0.70% 1.28% 0.38% 1.54% 1.14% 2.1% 1.0% 2.38%
i 7.529% 7.55% 6.25% 6.18% 10.01% 11.28% 8.27%* 5.1% 7.0% 6.50%
j 0.545% 0.27% 0.44% 0.40% 3.50% 0.00% 0.01% 0.7% 1.9% 1.46%
k 0.049% 1.21% 0.01% 0.02% 4.16% 0.00% 4.71% 3.2% 2.7% 2.25%
l 5.456% 3.44% 4.97% 2.78% 6.14% 6.51% 5.75% 5.2% 3.1% 3.57%
m 2.968% 2.53% 3.15% 4.74% 2.99% 2.51% 3.74% 3.5% 2.4% 2.21%
n 7.095% 9.78% 6.71% 5.05% 7.96% 6.88% 7.23% 8.8% 4.7% 10.03%
o 5.378% 2.51% 8.68% 10.73% 8.78% 9.83% 2.45% 4.1% 7.1% 6.06%
p 3.021% 0.79% 2.51% 2.52% 2.74% 3.05% 0.79% 1.7% 2.4% 1.57%
q 1.362% 0.02% 0.88% 1.20% 0.00% 0.51% 0 0.007% - 0.009%
r 6.553% 7.00% 6.87% 6.53% 5.91% 6.37% 6.95% 8.3% 3.5% 6.41%
s 7.948% 7.27% 7.98% 7.81% 6.09% 4.98% 2.95% 6.3% 3.8% 3.73%
t 7.244% 6.15% 4.63% 4.74% 5.27% 5.62% 3.09% 8.7% 2.4% 6.79%
u 6.311% 4.35% 3.93% 4.63% 3.18% 3.01% 3.43% 1.8% 1.8% 1.99%
v 1.628% 0.67% 0.90% 1.67% 1.90% 2.10% 0.98% 2.4% - 2.85%
w 0.114% 1.89% 0.02% 0.01% 0.00% 0.00% 0 0.03% 3.6% 1.52%
x 0.387% 0.03% 0.22% 0.21% 0.00% 0.00% 0 0.1% - 0.04%
y 0.308% 0.04% 0.90% 0.01% 0.00% 0.00% 3.37% 0.6% 3.2% 0.035%
z 0.136% 1.13% 0.52% 0.47% 0.50% 0.49% 1.50% 0.02% 5.1% 1.39%
à 0.486% 0 0 see a 0 see a 0 0.0% 0 see a
å 0 0 0 0 0 0 0 1.6% 0 -
ä 0 - 0 0 0 0 0 2.1% 0 see a
ą 0 - 0 0 0 0 0 0 see a -
œ 0.018% 0 0 0 0 0 0 0 0 -
ç 0.085% 0 0 see c 0 0 1.26% 0 0 -
ĉ 0 0 0 0 0.66% 0 0 0 0 -
ć 0 - 0 0 0 0 0 0 see c -
è 0.271% 0 0 0 0 see e 0 0.0% 0 see e
é 1.904% 0 0 see e 0 see e 0 0.0% 0 see e
ê 0.225% 0 0 see e 0 0 0 0 0 -
ë 0.001% 0 0 0 0 0 0 0 0 see e
ę 0 - 0 0 0 0 0 0 see e -
ĝ 0 0 0 0 0.69% 0 0 0 0 -
ğ 0 0 0 0 0 0 1.13% 0 0 -
ĥ 0 0 0 0 0.02% 0 0 0 0 -
î 0.045% 0 0 0 0 0 0 0 0 -
ì 0 0 0 0 0 see i 0 0 0 see i
ï 0.005% 0 0 0 0 0 0 0 0 see i
ı 0 0 0 0 0 0 5.20%* 0 0 -
ĵ 0 0 0 0 0.12% 0 0 0 0 -
ł 0 - 0 0 0 0 0 0 see l -
ñ 0 0 0.31% 0 0 0 0 0 0 -
ń 0 - 0 0 0 0 0 0 see n -
ò 0 0 0 0 0 see o 0 0 0 see o
ö 0 - 0 0 0 0 0.87% 1.5% 0 see o
ó 0 - 0 see o 0 0 0 0 see o see o
ŝ 0 0 0 0 0.38% 0 0 0 0 -
ş 0 0 0 0 0 0 1.94% 0 0 -
ś 0 - 0 0 0 0 0 0 see s -
ß 0 0.31% 0 0 0 0 0 0 0 -
ù 0.058% 0 0 0 0 see u 0 0 0 see u
ŭ 0 0 0 0 0.52% 0 0 0 0 -
ü 0 - 0 0 0 0 1.99% 0 0 see u
ź 0 - 0 0 0 0 0 0 see z -
ż 0 - 0 0 0 0 0 0 0.7% -

*See Turkish dotted and dotless I

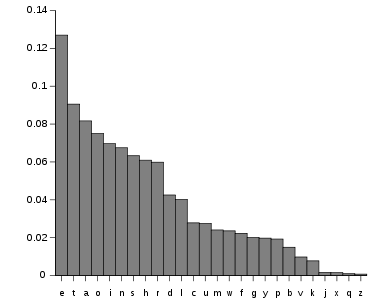
The figure below illustrates the frequency distributions of the 26 most common Latin letters across some languages.

Based on these tables, the 'etaoin shrdlu'-equivalent results for each language is as follows:

  • French: 'esait nrulo'; (Indo-European: Romance; traditionally, 'esartinulop' is used, in part for its ease of pronunciation[14])
  • Spanish: 'eaosr nidlc'; (Indo-European: Romance)
  • Portuguese: 'aeosr indmt' (Indo-European: Romance)
  • Italian: 'eaion lrtsc'; (Indo-European: Romance)
  • Esperanto: 'aieon lsrtk' (artificial language – influenced by Indo-European languages, Romance, Germanic mostly)
  • German: 'enisr atdhu'; (Indo-European: Germanic)
  • Swedish: 'eantr slido'; (Indo-European: Germanic)
  • Turkish: 'aeinr ldkmu'; (Turkic: a non Indo-European language)
  • Dutch: 'enati rodsl'; (Indo-European: Germanic)[15]
  • Polish: 'aoiez nscwr'; (Indo-European: Slavic)

All these languages use a basically similar 25+ character alphabet.

See also

References

  1. ^ Zim, Herbert Spencer. Codes and secret writing (abridged edition). Scholastic Book Services, fourth printing, 1962. Copyright 1948 Herbert S. Zim. Originally published by William Morrow.
  2. ^ Beker, Henry; Piper, Fred (1982). Cipher Systems: The Protection of Communications. Wiley-Interscience. p. 397.  Table also available from Lewand, Robert (2000). Cryptological Mathematics. The Mathematical Association of America. p. 36. ISBN 978-0883857199. http://books.google.com/books?id=CyCcRAm7eQMC&pg=PA36.  and [1]
  3. ^ Lee, E. Stewart; Essays about Computer Security; University of Cambridge Computer Laboratory, p. 181
  4. ^ Calculated from "Project Gutenberg Selections" available from the NLTK Corpora
  5. ^ "CorpusDeThomasTempé". http://gpl.insa-lyon.fr/Dvorak-Fr/CorpusDeThomasTemp%C3%A9. Retrieved 2007-06-15. 
  6. ^ Albrecht Beutelspacher, Kryptologie, 7. Aufl., Wiesbaden: Vieweg Verlagsgesellschaft, 2005, ISBN 3-8348-0014-7, p.10
  7. ^ Fletcher Pratt, Secret and Urgent: the Story of Codes and Ciphers Blue Ribbon Books, 1939, pp. 254-255.
  8. ^ "Frequência da ocorrência de letras no Português". http://www.numaboa.com/criptografia/criptoanalise/310-Frequencia-no-Portugues. Retrieved 2009-06-16. 
  9. ^ "La Oftecoj de la Esperantaj Literoj". http://lingvakritiko.com/2007/09/13/literoftecoj-kaj-tabelvortoftecoj/. Retrieved 2007-09-14. 
  10. ^ Simon Singh, Codici e Segreti, 1999, RCS, ISBN 88-17-12539-3
  11. ^ Simon Singh, Kodboken, 1999, Norstedts, ISBN 91-1-1300708-4
  12. ^ Wstęp do kryptologii, counting [space] 17.2%, [dot point] 0.9%, [comma] 0.9% and [semicolon] 0.5%
  13. ^ "Letterfrequenties". Genootschap OnzeTaal. http://www.onzetaal.nl/advies/letterfreq.php. Retrieved 2009-05-17. 
  14. ^ Perec, Georges; Alphabets; Éditions Galilée, 1976
  15. ^ "Letterfrequenties". Genootschap OnzeTaal. http://www.onzetaal.nl/advies/letterfreq.php. Retrieved 2008-12-26. 
Notes

Some useful tables for single letter, digram, trigram, tetragram, and pentagram frequencies based on 20,000 words that take into account word-length and letter-position combinations for words 3 to 7 letters in length. The references are as follows:

  • 1. Mayzner, M.S. & Tresselt, M.E. Tables of single-letter and digram frequency counts for various word-length and letter-position combinations. Psychonomic Monograph Supplements, 1965, 1, #2, 13-32.
  • 2. Mayzner, M.S., Tresselt, M.E. & Wolin, B.R. Tables of trigram frequency counts for various word-length and letter-position combinations. Psychonomic Monograph Supplements, 1965, 1, #3, 33-78.
  • 3. Mayzner, M.S., Tresselt, M.E. & Wolin, B.R. Tables of tetragram frequency counts for various word-length and letter-position combinations. Psychonomic Monograph Supplements, 1965, 1, #4, 79-143.
  • 4. Mayzner, M.S., Tresselt, M.E. & Wolin, B.R. Tables of pentagram frequency counts for various word-length and letter-position combinations. Psychonomic Monograph Supplements, 1965, 1, #5, 144-190.

External links


Wikimedia Foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Look at other dictionaries:

  • Letter frequency distribution for a sample English text — ▪ Table Letter frequency distribution for a sample English text letter number of occurrences frequency letter number of occurrences frequency E 8,915 .127 Y 1,891 .027 T 6,828 .097 U 1,684 .024 I 5,260 .075 M 1,675 .024 A 5,161 .073 F 1,488 .021… …   Universalium

  • Frequency analysis — In cryptanalysis, frequency analysis is the study of the frequency of letters or groups of letters in a ciphertext. The method is used as an aid to breaking classical ciphers.this is wrong is based on the fact that, in any given stretch of… …   Wikipedia

  • Letter frequencies — The frequency of letters in text has often been studied for use in cryptography, and frequency analysis in particular. No exact letter frequency distribution underlies a given language, since all writers write slightly differently. Linotype… …   Wikipedia

  • Frequency distribution — In statistics, a frequency distribution is an arrangement of the values that one or more variables take in a sample. Each entry in the table contains the frequency or count of the occurrences of values within a particular group or interval, and… …   Wikipedia

  • Letter beacon — Signal of letter beacon D on 5137.5 kHz Letter beacons are radio transmissions of uncertain origin, which consist of only a single repeating Morse Code letter. They are also often referred to as: SLB, or Single Letter Beacons SLHFB, or… …   Wikipedia

  • Frequency — For other uses, see Frequency (disambiguation). Three cyclically flashing lights, from lowest frequency (top) to highest frequency (bottom). f is the frequency in hertz (Hz), meaning the number of cycles per second. T is the period in seconds (s) …   Wikipedia

  • Letter case — For the minimalist musical sub genre, see Lowercase (music). For New Testament minuscules, see Category:Greek New Testament minuscules. Williamsburg eighteenth century press letters In orthography and typography, letter case (or just case) is the …   Wikipedia

  • Frequency list — In computational linguistics, a frequency list is a sorted list of words (word types) together with their frequency, where frequency here usually means the number of occurrences in a given corpus. A short example could be: the3789654he 2098762 [ …   Wikipedia

  • frequency illusion — n. The tendency to notice instances of a particular phenomenon once one starts to look for it, and to therefore believe erroneously that the phenomenon occurs frequently. Example Citations: The word issues bothers a fair number of people,… …   New words

  • What's the Frequency, Kenneth? — Infobox Single Name = What s the Frequency, Kenneth? Artist = R.E.M. Album = Monster Released = September 5, 1994 Format = Maxi single, CD single, 12 single, 7 single, cassette Recorded = October 1994 Genre = Alternative rock Length = 4:00 Label …   Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”