Crystallographic restriction theorem

The crystallographic restriction theorem in its basic form was based on the observation that the rotational symmetries of a crystal are usually limited to 2-fold, 3-fold, 4-fold, and 6-fold. However, quasicrystals can occur with other symmetries, such as 5-fold; these were not discovered until 1982, when a diffraction pattern out off a quasicrystal was first seen by the Israeli scientist Dan Shectman, who won the 2011 Nobel Prize in Chemistry for his discovery. ^[1]

Prior to the discovery of quasicrystals, crystals were modeled as discrete lattices, generated by a list of independent finite translations (Coxeter 1989). Because discreteness requires that the spacings between lattice points have a lower bound, the group of rotational symmetries of the lattice at any point must be a finite group. The strength of the theorem is that not all finite groups are compatible with a discrete lattice; in any dimension, we will have only a finite number of compatible groups.

Dimensions 2 and 3

The special cases of 2D (wallpaper groups) and 3D (space groups) are most heavily used in applications, and we can treat them together.

Lattice proof

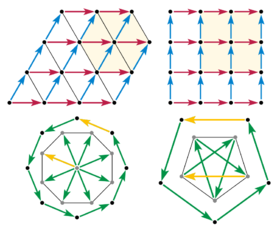
A rotation symmetry in dimension 2 or 3 must move a lattice point to a succession of other lattice points in the same plane, generating a regular polygon of coplanar lattice points. We now confine our attention to the plane in which the symmetry acts (Scherrer 1946). (We might call this a proof in the style of Busby Berkeley, with lattice vectors rather than pretty ladies dancing and swirling in geometric patterns.)

Lattices restrict polygons
 Compatible: 6-fold (3-fold), 4-fold (2-fold)
 Incompatible: 8-fold, 5-fold

Now consider an 8-fold rotation, and the displacement vectors between adjacent points of the polygon. If a displacement exists between any two lattice points, then that same displacement is repeated everywhere in the lattice. So collect all the edge displacements to begin at a single lattice point. The edge vectors become radial vectors, and their 8-fold symmetry implies a regular octagon of lattice points around the collection point. But this is impossible, because the new octagon is about 80% smaller than the original. The significance of the shrinking is that it is unlimited. The same construction can be repeated with the new octagon, and again and again until the distance between lattice points is as small as we like; thus no discrete lattice can have 8-fold symmetry. The same argument applies to any k-fold rotation, for k greater than 6.

A shrinking argument also eliminates 5-fold symmetry. Consider a regular pentagon of lattice points. If it exists, then we can take every other edge displacement and (head-to-tail) assemble a 5-point star, with the last edge returning to the starting point. The vertices of such a star are again vertices of a regular pentagon with 5-fold symmetry, but about 60% smaller than the original.

Thus the theorem is proved.

The existence of quasicrystals and Penrose tilings shows that the assumption of a linear translation is necessary. Penrose tilings may have 5-fold rotational symmetry and a discrete lattice, and any local neighborhood of the tiling is repeated infinitely many times, but there is no linear translation for the tiling as a whole. And without the discrete lattice assumption, the above construction not only fails to reach a contradiction, but produces a (non-discrete) counterexample. Thus 5-fold rotational symmetry cannot be eliminated by an argument missing either of those assumptions. A Penrose tiling of the whole (infinite) plane can only have exact 5-fold rotational symmetry (of the whole tiling) about a single point, however, whereas the 4-fold and 6-fold lattices have infinitely many centres of rotational symmetry.

Trigonometry proof

Consider two lattice points A and B separated by a translation vector r. Consider an angle α such that a rotation of angle α about any lattice point is a symmetry of the lattice. Rotating about point B by α maps point A to a new point A'. Similarly, rotating about point A by α, in the opposite direction, maps B to a point B'. Since both rotations mentioned are symmetry operations, A' and B' must both be lattice points. Due to periodicity of the crystal, the new vector r' which connects them must be equal to an integral multiple of r:

r' = mr

The four translation vectors (three of which are given by r, and one which connects A' and B' given by r') form a parallelogram. Therefore, the length of r' is also given by:

r' = -2rcos(α) + r

Combining the two equations gives:

cos(α) = (1 - m)/2 = M/2

Where M = 1-m is also an integer. Since we always have:

| cos(α) | ≤ 1

it follows that:

| M | ≤ 2

It can be shown that the only values of α in the 0° to 180° range that satisfy the three equations above are 0°, 60°, 90°, 120°, and 180°. In terms of radians, the only allowed rotations consistent with lattice periodicity are given by 2π/n, where n = 1, 2, 3, 4, 6. This corresponds to 1-, 2-, 3-, 4-, and 6-fold symmetry, respectively, and therefore excludes the possibility of 5-fold or greater than 6-fold symmetry.

Short trigonometry proof

Consider a line of atoms A-O-B, separated by distance t. Rotate the entire row by +2π/n and -2π/n, with point O kept fixed. Due to the assumed periodicity of the lattice, the two lattice points C and D will be also in a directly below the initial row; moreover C and D will be separated by r = mt, with m an integer. But by the geometry, the separation between these points is 2tcos(2π/n). Equating the two relations gives 2cos(2π/n) = m. This is satisfied by only n = 1, 2, 3, 4, 6. (See also the sketch in section Preuve mathématique simple of the French Wikipedia article (Théorème de restriction cristallographique)

Matrix proof

For an alternative proof, consider matrix properties. The sum of the diagonal elements of a matrix is called the trace of the matrix. In 2D and 3D every rotation is a planar rotation, and the trace is a function of the angle alone. For a 2D rotation, the trace is 2 cos θ; for a 3D rotation, 1 + 2 cos θ.

Examples

• Consider a 60° (6-fold) rotation matrix with respect to an orthonormal basis in 2D.

$\begin{bmatrix} {1/2} & -{\sqrt{3}/2} \\ {\sqrt{3}/2} & {1/2} \end{bmatrix}$

The trace is precisely 1, an integer.

• Consider a 45° (8-fold) rotation matrix.

$\begin{bmatrix} {1/\sqrt{2}} & -{1/\sqrt{2}} \\ {1/\sqrt{2}} & {1/\sqrt{2}} \end{bmatrix}$

The trace is 2/√2, not an integer.

Using a lattice basis, neither orthogonality nor unit length is guaranteed, only independence. However, the trace is the same with respect to any basis. (Similarity transforms preserve trace.) In a lattice basis, because the rotation must map lattice points to lattice points, each matrix entry — and hence the trace — must be an integer. Thus, for example, wallpaper and crystals cannot have 8-fold rotational symmetry. The only possibilities are multiples of 60°, 90°, 120°, and 180°, corresponding to 6-, 4-, 3-, and 2-fold rotations.

Example

• Consider a 60° (360°/6) rotation matrix with respect to the oblique lattice basis for a tiling by equilateral triangles.

$\begin{bmatrix} 0 & -1 \\ 1 & 1 \end{bmatrix}$

The trace is still 1. The determinant (always +1 for a rotation) is also preserved.

The general crystallographic restriction on rotations does not guarantee that a rotation will be compatible with a specific lattice. For example, a 60° rotation will not work with a square lattice; nor will a 90° rotation work with a rectangular lattice.

Higher dimensions

When the dimension of the lattice rises to four or more, rotations need no longer be planar; the 2D proof is inadequate. However, restrictions still apply, though more symmetries are permissible. For example, the hypercubic lattice has an eightfold rotational symmetry, corresponding to an eightfold rotational symmetry of the hypercube. This is of interest, not just for mathematics, but for the physics of quasicrystals under the cut-and-project theory. In this view, a 3D quasicrystal with 8-fold rotation symmetry might be described as the projection of a slab cut from a 4D lattice.

The following 4D rotation matrix is the aforementioned eightfold symmetry of the hypercube (and the cross-polytope):

$A = \begin{bmatrix} 0 & 0 & 0 & -1 \\ 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \end{bmatrix}.$

Transforming this matrix to the new coordinates given by

$B = \begin{bmatrix} -1/2 & 0 & -1/2 & \sqrt 2/2 \\ 1/2 & \sqrt 2/2 & -1/2 & 0 \\ -1/2 & 0 & -1/2 & -\sqrt 2/2 \\ -1/2 & \sqrt 2/2 & 1/2 & 0 \end{bmatrix}$ will produce:

$B A B^{-1} = \begin{bmatrix} \sqrt 2/2 & \sqrt 2/2 & 0 & 0 \\ -\sqrt 2/2 & \sqrt 2/2 & 0 & 0 \\ 0 & 0 & -\sqrt 2/2 & \sqrt 2/2 \\ 0 & 0 & -\sqrt 2/2 & -\sqrt 2/2 \end{bmatrix}.$

This third matrix then corresponds to a rotation both by 45° (in the first two dimensions) and by 135° (in the last two). Projecting a slab of hypercubes along the first two dimensions of the new coordinates produces an Ammann–Beenker tiling (another such tiling is produced by projecting along the last two dimensions), which therefore also has 8-fold rotational symmetry on average.

The A4 lattice and F4 lattice have order 10 and order 12 rotational symmetries, respectively.

To state the restriction for all dimensions, it is convenient to shift attention away from rotations alone and concentrate on the integer matrices (Bamberg, Cairns & Kilminster 2003). We say that a matrix A has order k when its k-th power (but no lower), A^k, equals the identity. Thus a 6-fold rotation matrix in the equilateral triangle basis is an integer matrix with order 6. Let Ord_N denote the set of integers that can be the order of an N×N integer matrix. For example, Ord₂ = {1, 2, 3, 4, 6}. We wish to state an explicit formula for Ord_N.

Define a function ψ based on Euler's totient function φ; it will map positive integers to non-negative integers. For an odd prime, p, and a positive integer, k, set ψ(p^k) equal to the totient function value, φ(p^k), which in this case is p^k−p^k−1. Do the same for ψ(2^k) when k > 1. Set ψ(2) and ψ(1) to 0. Using the fundamental theorem of arithmetic, we can write any other positive integer uniquely as a product of prime powers, m = ∏_α p_α^{k _α}; set ψ(m) = ∑_α ψ(p_α^{k _α}). This differs from the totient itself, because it is a sum instead of a product.

The crystallographic restriction in general form states that Ord_N consists of those positive integers m such that ψ(m) ≤ N.

Smallest dimension for a given order A080737

m	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31
ψ(m)	0	0	2	2	4	2	6	4	6	4	10	4	12	6	6	8	16	6	18	6	8	10	22	6	20	12	18	8	28	6	30

Note that these additional symmetries do not allow a planar slice to have, say, 8-fold rotation symmetry. In the plane, the 2D restrictions still apply. Thus the cuts used to model quasicrystals necessarily have thickness.

Integer matrices are not limited to rotations; for example, a reflection is also a symmetry of order 2. But by insisting on determinant +1, we can restrict the matrices to proper rotations.

Formulation in terms of isometries

The crystallographic restriction theorem can be formulated in terms of isometries of Euclidean space. A set of isometries can form a group. By a discrete isometry group we will mean an isometry group that maps every point to a discrete subset of R^N, i.e. a set of isolated points. With this terminology, the crystallographic restriction theorem in two and three dimensions can be formulated as follows.

For every discrete isometry group in two- and three-dimensional space which includes translations spanning the whole space, all isometries of finite order are of order 1, 2, 3, 4 or 6.

Note that isometries of order n include, but are not restricted to, n-fold rotations. The theorem also excludes S₈, S₁₂, D_4d, and D_6d (see point groups in three dimensions), even though they have 4- and 6-fold rotational symmetry only.

Note also that rotational symmetry of any order about an axis is compatible with translational symmetry along that axis.

The result in the table above implies that for every discrete isometry group in four- and five-dimensional space which includes translations spanning the whole space, all isometries of finite order are of order 1, 2, 3, 4, 5, 6, 8, 10, or 12.

All isometries of finite order in six- and seven-dimensional space are of order 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 18, 20, 24 or 30 .

See also

• Crystallographic point group
• Crystallography

Notes

1. ^ Shechtman et al (1982)

References

• Bamberg, John; Cairns, Grant; Kilminster, Devin (March 2003), "The crystallographic restriction, permutations, and Goldbach's conjecture", American Mathematical Monthly 110 (3): 202–209, doi:10.2307/3647934, JSTOR 3647934, http://www.latrobe.edu.au/mathstats/staff/cairns/papers/42.pdf 
• Elliott, Stephen (1998), The Physics and Chemistry of Solids, Wiley, ISBN 0-471-98194-X 
• Coxeter, H. S. M. (1989), Introduction to Geometry (2nd ed.), Wiley, ISBN 978-0-471-50458-0 
• Scherrer, W. (1946), "Die Einlagerung eines regulären Vielecks in ein Gitter", Elemente der Mathematik 1 (6): 97–98, http://www-gdz.sub.uni-goettingen.de/cgi-bin/digbib.cgi?PPN378850199_0001 
• Shechtman, D.; Blech, I.; Gratias, D.; Cahn, JW (1984), "Metallic phase with long-range orientational order and no translational symmetry", Physical Review Letters 53 (20): 1951–1953, Bibcode 1984PhRvL..53.1951S, doi:10.1103/PhysRevLett.53.1951 

External links

• The crystallographic restriction