Blood flow

Blood flow is the continuous running of blood in the cardiovascular system. The human body is made up of several processes all carrying out various functions. We have the gastrointestinal system which aids the digestion and the absorption of food. We also have the respiratory system which is responsible for the absorption of O₂ and elimination of CO₂ .The urinary system removes waste from the body. The cardiovascular system helps to distribute food, O₂ and other product of metabolism. The reproductive system is also worth mentioning, this system is responsible for perpetuating the species. The nervous and endocrine system is responsible for coordinating the integration and function of other system.

Cell «»Tissue«»Organ«»System.

The cell as we know from elementary science is the basic structure in the human body. These cells that makes up the bodies of all living things exist in an ‘internal sea’ of extracellular fluid (ECF) enclosed within the integument of the animal. From this fluid, the cell takes up O₂ and nutrients into it, they discharge metabolic waste products. In animals with a closed vascular system, the ECF is divided into two components, the interstitial fluid and the circulating blood plasma. The plasma and the cellular elements of the blood, principally red blood cells, fill the vascular system and together they constitute the total blood volume.^[1]

Blood and its Composition.

Basically blood is the viscous fluid composed of plasma and cells. The composition of the blood includes plasma, red blood cells, white blood cells and platelets. In the microcirculation the properties of the blood cells have an important influence on flow.

Plasma

The plasma constitutes between 52 and 62% of the whole blood. It is straw-coloured in which blood cells, proteins and other substances are suspended and transported. Water constitutes 91.5% of plasma. Proteins from which plasma fractions are derived constitute 7% of the plasma (these include also albumins, which makes up about 4% of the plasma, globulins, about 3% and fibrinogen, less than 1%). The remaining 1.5% of plasma is made up of other substances such as nutrients, hormones, respectively gases, electrolytes, vitamins and nitrogenous wastes.

White Blood Cell

The white blood cells are also referred to as the leucocytes. The leucocytes (the white blood cells) constitute less than 1% of the total blood cell volume in humans.The basic function of the leucocytes is to attack and destroy potentially harmful foreign matter. The diameter of the leucocytes varies from 6 to 7.5μm.^[2] The presence of shunt vessels in organs facilitates the transportation of white blood cells through those organs. In arterioles the leucocytes tend to flow in the vessels with the highest flow velocity.

Platelets

Also referred to as the thrombocytes.They occupy even less volume than the leucocytes. The thrombocytes constitute of less than 1% of whole blood volume. These are responsible for forming clot, blocking blood from exiting wounds. Usually the platelets have very little effects on the bulk viscosity of blood. Platelets are disc-shaped and have a long axis of about 3μm and a thickness of 0.6-1.0μm.^[2]

Red Blood Cell

The red blood cells also called the erythrocytes.These constitute between 38 and 48% of the whole blood. These cells keep the tissue alive by bringing oxygen to it and taking carbon dioxide away. Unstressed, normal human red blood cells are biconcave disc with a long axis of approximately 8μm and a thickness of 2μm. RBCs can change their shape remarkably well as they pass through capillaries while the membrane of the RBC often rotates relatively quickly around the cytoplasm. The RBC is like a bag that can be deformed into almost any shape due to an excess surface area for its volume.^[2]

The Mechanics of Blood Circulation

Basically mechanics is the study of motion (or equilibrium) and the forces that causes it. The blood moves in the blood vessels, while the heart serves as the pump for the blood. The vessel walls of the heart are elastic and are movable, therefore causing the blood and the wall to exert forces on each other which in turn influence their respective motion. Therefore to understand the mechanics of circulation of the heart, it will be worth the while to go through a review of basic mechanics of fluid, and elastic solids (momentum) and the nature of the forces exerted between two moving substances in contact.

The Basics of Motion

The study of motion is born from the argument that there is no change in motion without force. These believes where some what obscured until the seventeenth century when Isaac Newton formulated his three laws of motion.

Position

Before talking about motion successfully we must be able to describe accurately a fluid particles position in space, which changes as the particles moves. The Cartesian plane can be used as a beautiful way of illustrating the position of any object in space.

Velocity

Another quantity of interest in describing the motion of a particle is its velocity. The velocity basically is the rate of change of the position of an object with time.

$v = \frac{\Delta x}{\Delta t}$

Acceleration

The rate of change of position as we saw is the velocity. While the rate of change of velocity is referred to as the acceleration. For a motion along a line, the acceleration is given as:

$a = \frac{\Delta v}{\Delta t}$

This is the same as the slope of the tangent of the graph v against t. The unit of acceleration is meter per seconds squared.(ms-2).

Newton's Laws of Motion

Newton’s first law: every particle continues in a state of rest of uniform motion in a straight line unless acted on by some external force or forces. In other words the velocity remains constant (zero acceleration) if no force is acting on the body. Newton’s second law: when a particle of mass m is acted on by a force so that it experiences an acceleration a, the net force acting on it is equal to the mass multiplied by the acceleration. That is to say the net force is a vector which we can call F. which is given by F= ma This equation is an important equation in mechanics. It is called the equation of motion of a particle. The term net force means the sum of all forces acting on the particle, which may be exerted in different ways. Newton’s third law: Newton’s third law has commonly been described as action and reaction. Basically the law is defined as, to every action there is equal and opposite reaction. That is to say, if one body exerts a force F on another body, the second body must also exerts an equal and opposite reaction on the formal body (-F). The negative on the force by no means suggest that force can be negative, the negative only means that the force is acting on the opposite direction, it has nothing to do with the magnitude it is simply the direction. As an illustration if you press a stone to your finger, unknown to you, your finger exerts a force also on the stone which is equal in magnitude.

Momentum

we recall from Newton’s second law that F= ma When expanded the above can be written as

$F =m{\mathrm{d}\mathbf{v}\over\mathrm{d}t}$

$\mathbf{F} = {\mathrm{d}(m \mathbf{v}) \over \mathrm{d}t}$.

The quantity mv is called the momentum of a particle. Therefore we can also say that Newton’s law from the equation above can be defined as force and is equal to the rate of change of momentum. In the absence of external forces the momentum of a particle of a body or system of particle remains constant or is conserved. What we mean is that, if two particles (masses m1 and m2) and velocities v_1 and v_2 collides, the combined body (m_1 + m_2 ) must have the same momentum as the original body put together, so its velocities must be (m_1v_1 + m_2v_2)/ m_1 +m_2. If the collision is instantaneous this would be true immediately. Thus we also have inelastic and elastic collision depending on the relative motion of the masses, or continuous.

Basic Ideas In Fluid Mechanics

Basically the force experienced by fluids includes long range and short range. The long range force includes gravitational and electromagnetic forces. The electromagnetic force on an element depends on the quantities like its electric charge, but on the other hand the gravitational force depends only on its mass. We will consider from this point the gravitational force alone. If we have a fluid with element p which occupies the point x at a certain time t and has a volume v and if the fluid in the neighbourhood of x, at that time has a density ϼ then the gravitational force on the element is given as

ϼ v g

Stress

When we apply force to a material basically it starts to deform or move. As the force that is needed to deform a material (=let a fluid flow) increases with the size of the surface of the material A.^[3] The magnitude of this force F is proportional to the area A of the portion of the surface. Therefore the quantity (F/A) that is the force per unit area is called the stress.

$\sigma = \frac{F}{A}$.

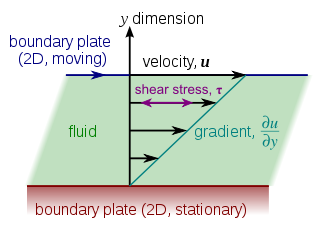Laminar shear of fluid between two plates. v = u,τ = σ. Friction between the fluid and the moving boundaries causes the fluid to shear (=flow). The force required for this action per unit area is the stress. The relation between the stress (=force) and the shear rate (=flow velocity) determines the viscosity.

Hydrostatic pressure

In a stationary fluid the only stress present is the pressure. Let us assume a body force that is vertical, we can assume the horizontal component of the pressure force must balance out. Pressure varies with height as we know, as we move the height the pressure changes.^[4] If A is the horizontal cross-sectional area of the element and if p1 and p_2 are the pressure on the surface, where p1 is the pressure on the bottom and p2 is the pressure on the top, then the net upward force on the element can be given as (p_1 – p_2 )A This must be equal to the weight which acts downwards and is equal to the density of the fluid times its volume ( AZ’) where Z’ is the depth of the element times g. (p_1 – p_2 )A = gϼAZ’ (p_1 – p_2 ) = gϼZ’ If we assume that the pressure is atmospheric and assuming Z=0 that is to say Z is negative in the fluid. While p is given as P_1 = p_2 - gϼZ The above equation there is the called the hydrostatic pressure

Viscosity

The magnitude of the viscous stresses depends upon the rate of deformation. For example when a body is moved rapidly through a fluid it causes more rapid deformation of fluid element than one moving slowly. Viscosity is giving as:

$\tau=\mu \frac{\partial u}{\partial z}$

where mu is a constant called the coefficient of viscosity^[3]

Conservation of Mass

Basically before we discuss anything on the circulation of blood there are two principles we must discuss. The first is the conservation of mass. These principles of conservation states that mass can neither be created nor destroyed (well there is an exception though in nuclear reactions). The implication of this therefore is that the same mass of fluid must flow out of a system tubes as the same mass of fluid that flows in, unless either the density of the fluid inside increases (so that a greater mass occupies the same volume), or the volume of the system of tubes increases though the expansion of flexible walls. All fluids can be treated as incompressible. We only assume that gases are compressible. These approximation breaks down when the fluid speed approaches the speed of sound in the fluid. But in the circulation of blood that we are concern with, the maximum blood velocities observed are well below 1% of sound speed. Therefore we can say that blood is an incompressible fluid. Therefore we can rightly say that if blood flows into a tube what flows out must be the same as what flows in. therefore a tube of cross sectional area A the speed of the flow at any time will vary along its length. The product of the area A with the velocity is called the volume flow rate.

$Q = u \cdot A$

This is related to the mass flowrate as

$M = p \cdot Q$

where M is the mass flowrate

p is the density

Q volumetric flow rate

Bernoulli’s equation

The second general principle concerns the conservation of energy. Recall the laws of thermodynamics, it states that the rate of change of the total energy of a system is equal to the rate at which applied force do work on it. When there are no applied forces, the total energy is constant i.e. energy is conserved. We can introduce the idea of a streamline. Consider a steady flow in which its boundary consists of a streamline. If we assume that the fluid is constrain to remain on the streamline and if we assume the two ends of a finite length of the tube are at different levels and the fluid is flowing up from an initial velocity u₁ and a cross sectional area A₁ to a level Z₂ with velocity u² and area A₂ therefore we can have the Bernoulli’s equation given as

p₁ + 0.5ρ(u₁)² + ρgZ₁ = p₂ + 0.5ρ(u₁)² + ρgZ₂

where p is the pressure,
u is the velocity,
Z is the height.

The mechanics of Blood

The flow measurement as well as the mechanics of blood itself is a very broad topic, we will only give a brief overview of what is contained therein. The mechanical property of blood which is of interest to us is the viscosity.

Viscosity of the Plasma

Normal plasma behaves like a Newtonian fluid at rates of shear. Typical values for the viscosity of normal human plasma at 37°C is 1.2Nsm-2. The viscosity of normal plasma varies with temperature in just the same way as does that of its solvent water, a 5°C increase of temperature in the physiological range reduces plasma viscosity by about 10%.

Osmotic Pressure of Plasma

The osmotic pressure of solution is determined by the number of particles present by the temperature. For example a 1 molar solution of a substance contains 6.022 x 10²³ molecules per liter of that substance and has at 0°C an osmotic pressure of 2.27MNm^-2 (22.4atm). The osmotic pressure of the plasma affects the mechanics of the circulation in several ways. An alteration of the osmotic pressure difference across the membrane of a blood cell will cause a shift of water and a change of the cell volume. The change both in shape and flexibility will affect the mechanical properties of whole blood. A change therefore in plasma osmotic pressure will alter the hematocrit that is the volume concentration of red cells in the whole blood by redistributing water between the intravascular and extravascular spaces. This in turn will affect the mechanics of the whole blood.^[3]

The red Cells

The red cell is highly flexible bi-concave disc. The red cell membrane has a young modulus in the region of 106 Nm^-2 . The deformation in the red cells is induced by the shear stress. When a suspension is sheared the red cells are seen to deform and spin, because of the velocity gradient, but the rate of deformation and spin depends on the shear-rate and the concentration. This topic can influence the mechanics of the circulation and may complicate the measurement of the blood viscosity. It is true that in a steady state flow of a viscous fluid through a rigid spherical body immersed in the fluid where we assume the inertia is negligible in such a flow it is believed the downward gravitational force of the particle is balanced by the viscous drag force. From this force balance the speed of fall this can be shown to be given by Stokes' law

$U_s = \frac{2}{9}\frac{\left(\rho_p - \rho_f\right)}{\mu} g\, a^2$^[3]

Where a is the particle radius, ρ_p , ρ_f are the respectively particle and fluid density μ is the fluid viscosity, g is the gravitational acceleration. From the above equation we can see that the sedimentation velocity of the particle depends on the square of the radius. If the particle is released from rest in the fluid, its sedimentation velocity U_s increases until it attains the steady value called terminal velocity (U) as shown above. We have looked at blood flow, blood composition. Before we look at the main issue, hemodilution let us take a brief history into the use of blood. The therapeutic use of blood is not a modern phenomenon. Egyptian writings dates back at least 2000 years suggest oral ingestion of blood as a ‘sovereign remedy’ for leprosy. Experiments with the first intravenous blood transfusions began at the start of the 16th century, and in the last 50 years the field of transfusion medicine has progressed remarkably bringing with it an increase in the use of blood and blood product.^[5] However the therapeutic use of blood comes with its significant risks which are enormous. As a result many persons are searching for alternatives to transfusion of whole blood. Today bloodless medicine and surgery (BMS) programs have been developed not only for a group of people because of their religious believes but they are also sought after by patient who fear the risks of blood transfusion and desire the best medical care.

Hemodilution

Hemodilution is defined simply as the dilution of the concentration of red blood cells and plasma constituents by partially substituting the blood with colloids or crystalloids and it is a strategy to avoid exposure of patients to the hazards of homologous blood transfusions. Hemodilution can be normovolemia where as we said implies the dilution of the normal blood constituents by the use of expanders. During acute normovolemic hemodilution (ANH) blood subsequently lost during surgery contains proportionally fewer red blood cells per millimetre, thus minimizing intraoperative loss of the whole blood, therefore blood lost during surgery by the patient is not actually lost by the patient for this volume is purified and redirected into the patient. There is however the hypervolemic hemodilution (HVH) here instead of simultaneous exchanging the patient’s blood as in ANH, hypervolemic technique is carried out by the use of acute preoperative volume expansion without any blood removal. In choosing a fluid however we must be sure that when mixed the remaining blood behaves in the microcirculation as the original blood fluid retaining all its properties of viscosity.^[6] In presenting what volume of ANH should be applied one study suggest a mathematical model of ANH, which calculates the maximum possible RCM savings using ANH given the patients weight H_i and H_m. Not to worry. Attached to this document is a glossary of the term used. To maintain the normovolemia, the withdrawal of autologous blood must be simultaneously replaced by a suitable hemodilute.Ideally, this is achieved by isovolemia exchange transfusion of a plasma substitute with a colloid osmotic pressure (OP). A colloid is a fluid containing particles that are large enough to exert an oncotic pressure across the micro vascular membrane. When debating the use of colloid or crystalloid, it is imperative to think about all the components of the starling equation:

$\ Q = K ( [P_c - P_i]S - [P_c - P_i] )$

To identify the minimum safe hematocrit desirable for a given patient the following equation is useful:

$\ BL_s = EBV \ln \frac{H_i}{H_m}$

Where EBV is the estimated blood volume 70mL/kg was used in this model and Hi (initial hematocrit) is the patient’s initial hematocrit. From the equation above it is clear that the volume of blood removed during the ANH to the Hm is the same as the BLs. The collection of blood needed to be removed is usually based on the weight not volume. The number of units that needed to be removed to hemodilute to the maximum safe hematocrite (ANH) can be found by

$ANH = \frac {BL_s}{450}$

This is based on the assumption that each unit removed by hemodilution has a volume of 450mL (the actual volume of a unit will vary somewhat since completion of collection as we mentioned is dependent on weight and not volume). The model assumes that the hemodilute value to the Hm prior to surgery, therefore the re-transfusion of blood obtained by hemodilution must begin when SBL begins. The RCM available for retransfusion after ANH (RCMm) can be calculated from the patients Hi and the final hematocrit after hemodilution(H_m)

$RCM = EVB \times (H_i - H_m)$

While the maximum SBL that is possible when ANH is used without falling below Hm(BLH) is found by assuming that all the blood removed during ANH is returned to the patient at a rate sufficient to maintaining the hematocrit at the minimum safe level

$BL_H = \frac {RCM_H} {H_m}$

If ANH is used as long as SBL does not exceed BL_H there will not be any need for blood transfusion. We can conclude from the foregoing BL_H should therefore not exceed BL_s. The difference between the BL_H and the BLs therefore is the incremental surgical blood loss (BL_i) possible when using ANH.

$\ {BL_i} = {BL_H} - {BL_s}$

When expressed in terms of the RCM

${RCM_i} = {BL_i} \times {H_m}$

Where RCM_i is the red cell mass that would have to be administered using homologous blood to maintain the H_m if ANH is not used and blood loss equals BLH. The model used assumes ANH used for a 70 kg patient with an estimated blood volume of 70mL/kg (4900mL). A range of Hi and Hm were evaluated to understand condition where hemodilution is necessary to achieve benefit to the patient.^[7][8]

Result

The result of the model calculations are presented in a table given in the appendix for a range of Hi from 0.30 to 0.50 with ANH performed to minimum hematocrits from 0.30 to 0.15. Given a Hi of 0.40, if the H_m is assumed to be 0.25.then from the equation above RCM count is still high and ANH is not necessary, if BLs does not exceed 2303mL, since the hemotocrit will not fall below H_m. though 5units of blood must be removed during hemodilution. Under these conditions to achieve the maximum benefit from the technique and if ANH is used no homologous blood will be required to maintain the Hm if blood loss does not exceed 2940mL. In such a case ANH can save a maximum of 1.1 packed red blood cell unit equivalent, in such a case homologous blood transfusion will be necessary to maintain Hm even if ANH is used. This model can be used to identify when ANH may be used for a given patient and the degree of ANH necessary to maximize that benefit. For example if Hi is 0.30 or less it is not possible to save a red cell mass equivalent to 2 unit of homologous PRBC even if the patient is hemodiluted to an H_m of 0.15. That is because from the RCM equation the patient RCM falls short from the equation giving above. If Hi is 0.40 one must remove at least 7.5 units of blood during ANH, resulting in an Hm of 0.20 to save 2 units equivalence. Clearly the greater the Hi and the greater the amount of units removed during hemodilution, the more effective ANH is for preventing homologous blood transfusion. The model here is designed to allow doctors determine where ANH may be beneficial for a patient based on their knowledge of the H_i , the potential for SBL and estimate of the Hm. Though the model used a 70 kg patient, the result can be applied to any patient. To apply these result to any body weight any of the values BLs, BLH and ANHH or PRBC given in the table need to be multiplied by the factor we will call T

$T = \frac {70 \times patients weight in kg} {4900}$

Basically the model we have considered above is designed to predict the maximum RCM that can be saved ANH. In summary the efficacy of ANH has been described mathematically by means of measurements of surgical blood loss and blood volume flow measurement. This form of analysis permits accurate estimation of the potential efficiency of the techniques and it goes to show the application of measurement in the medical field.

Table

Initial hematocrit(H_i)	Minimum safe hematocrit(H_m)	Maximum blood loss without ANH	Maximum blood loss with ANH	0No units removed by ANH(ANH_u)	Packed red cell equivalents saved (PRBC)
0.50	0.30	2503	3267	5.6	1.5
0.50	0.25	3396	4900	7.5	2.5
0.50	0.20	4490	7350	10.0	3.8
0.50	0.15	5899	11433	13.1	5.5
0.45	0.30	1987	2450	4.4	0.9
0.45	0.25	2880	3920	6.4	1.7
0.45	0.20	3974	6125	8.8	2.9
0.45	0.15	5383	9800	11.9	4.4
0.40	0.30	1410	1633	3.1	0.4
0.40	0.25	2303	2940	5.1	1.1
0.40	0.20	3396	4900	7.5	2.0
0.40	0.15	4806	8167	10.7	3.4
0.35	0.30	755	817	1.7	0.1
0.35	0.25	1649	1960	3.7	0.6
0.35	0.20	2742	3675	6.1	1.2
0.35	0.15	4152	6533	9.2	2.4
0.30	0.30	0	0	0	0
0.30	0.25	893	980	2.0	0.2
0.30	0.20	1987	2450	4.4	0.6
0.30	0.15	3396	4900	7.5	1.5

Table Model calculations for Hypothetical 70 kg patient.^[7]

Glossary of Terms

ANH	Acute Normovolemic Hemodilution
BLH	Maximum Blood Loss Possible When ANH Is Used Before Homologous Blood Transfusion Is Needed.
BLI	Incremental Blood Loss Possible with ANH.(BLH – BLs)
BLs	Maximum blood loss without ANH before homologous blood transfusion is required
EBV	Estimated Blood Volume(70mL/kg)
Hct	Hamatocrit Always Expressed Here As A Fraction
Hi	Initial Haematocrit
Hm	Minimum Safe Haematocrit
PRBC	Packed Red Blood Cell Equivalent Saved by ANH
RCM	Red cell mass.
RCMH <cd Cell Mass Available For Transfusion after ANH
RCMI	Red Cell Mass Saved by ANH
SBL	Surgical Blood Loss

glossary of times used^[7]

References

1. ^ 'Jan S., & Westerhof N., (1993). the physics of heart and circulation. institute of physics publishing. pp. 1–13,121–148. ISBN 0-7503-0278-X. 
2. ^ ^{a b c} transfusion medicine-is its future secure?. 08. Awake. 2006. p. 8. ISSN 005-237X. 
3. ^ ^{a b c d} 'caro C.G, Pedley, T.J, Schroter R.C., Seed. W.A. (1978). tthe mechanics of circulation. oxford university press. pp. 3–60, 151–176. ISBN 0-19-263323-6. 
4. ^ 'Leon G., Peter H. & Andrew M.,' (1991). theory of heart, biomechanics,biophysics and nonlinear dynamics of cardiac function. springer-verlag New york inc. pp. 239–283. ISBN 0-387-974830. 
5. ^ "Bloodless medicine and surgery". http://jic.sagepub.com/content/14/1/20. Retrieved 5 April 2011. 
6. ^ "Efficacy of Acute Normovolemic hemodilution,Accessed as a Function of Blood lost". the journal of American society of anesthsiologist inc. http://journals.lww.com/anesthesiology/Abstract/2001/03000/Efficacy_of_Acute_Normovolemic_Hemodilution.13.aspx. Retrieved 5 April 2011. 
7. ^ ^{a b c} "Hemodilution:Modelling and clinincal Aspects". IEEE. http://ieeexplore.ieee.org/Xplore/login.jsp?reason=login&url=stamp%2Fstamp.jsp%3Ftp%3D%26arnumber%3D1018881. Retrieved 5 April 2011. 
8. ^ [http://www.anesthesia-analgesia.org/content/80/1/108.full.pdf+ html "maximum blood savings by acute Normovolemic hemodilution"]. anesthesia & analgesia the gold standard in anesthesiology. http://www.anesthesia-analgesia.org/content/80/1/108.full.pdf+ html. Retrieved 5 April 2011.