- Omweso
-
Omweso Ranks Four Sowing Multilap Region Uganda Omweso (sometimes shortened to Mweso) is the traditional mancala game of the Ugandan people. The game was supposedly introduced by the Bachwezi people of the ancient Bunyoro-kitara empire of Uganda. Nowadays the game is dominated by Ugandan villagers. It is a very hard and fast game said to keep one's mind high and ever excited[citation needed], which can make it addictive. The equipment needed for the game is essentially the same as that of the Bao game (found in Tanzania and neighbouring countries). Omweso is strictly related to a wide family of mancalas found in eastern and southern Africa; these include Coro in the Lango region of Uganda, Aweet in Sudan, [[1]] in Namibia, Kombe in Lamu (Kenya), Mongale in Mombasa (Kenya), Mongola in Congo, Igisoro in Rwanda, and Kiela in Angola.
The name "Omweso" is derived from Swahili word michezo, which means "game".
Contents
Rules
Equipment
Omweso requires a board of 32 pits, arranged with eight pits lengthwise towards the players, and four pits deep. Each player's territory is the 16 pits on their side of the board. In addition, 64 undifferentiated seeds are needed. This equipment is the same used for many variants of Omweso as well as for the Bao game from Zanzibar and Tanzania. Unlike Bao boards, Omweso boards have no special pit (nyumba).
Object
The normal way to win the game is to be the last player to be able to make a legal move, possible by capturing all an opponent's stones or reducing the opponent to no more than one seed in each pit. Alternatively, a player can win by capturing on both ends of the board in one turn.
Setup
Before the game, four (4) seeds are placed in each of the eight pits closest to a player or alternatively, two seeds in each and every pit – to ensure that both players have exactly 32 seeds. The first player is chosen by lot. This player arranges all owned seeds on their side of the board according to preference (The arrengment should be strategic). Then, the second player also arranges their seeds. The first player then makes the first sowing move.
Sowing
Example turn:
















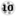















Preparing to sow from the highlighted hole.
















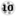















Sowing captures 6 seeds.
















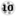















The 6 captured seeds are resown from the starting hole.
Play consists of turns, each of which may involve several moves. A player moves by selecting a pit with at least two seeds, and sowing them one by one around their side of the board in a counter-clockwise direction from the starting pit. The player may only sow from one of the sixteen pits in their territory, and the sowing proceeds around this territory, not directly involving the opponent's side.
Although in the past it was common for players to spend much time in thought, in modern tournaments only three seconds of thought is allowed per turn. The referee counts omu, ebiri, and if the turn is not started the other player may steal it.
Relay Sowing
If the last sowed seed lands in an occupied pit (without resulting in a capture, see below), then all seeds in that pit, including the one just placed, are immediately sown, before the opponent's turn. This continues until the last sowing ends in an empty pit.
Capturing
If the last seed sown lands in one of the player's eight inner pits, which is occupied, and furthermore both the opponent's pits in this same column are occupied, then all seeds from these two pits are captured and sown starting from the pit where this capturing move began (i.e., from the last pit scooped, NOT from the original hole from the very beginning of the turn).
Reverse Capturing
Instead of sowing in a counter-clockwise direction, a player may sow clockwise from any of their four leftmost pits if this results in a capture. Upon re-entering these reverse-captured seeds, the player may sow them clockwise again, if and only if this play results in a direct capture. The player may also choose to sow reverse-captured seeds in the usual counter-clockwise manner, and there is no compulsion to play one direction or the other when the choice is available. During a relay-sowing move, one leg of which ends at one of the four leftmost pits, a player may also change direction and begin sowing the next leg of the move clockwise, if and only if this play results in a direct capture.
Alternate victory conditions
The normal way to win the game is to be the last player left with a legal move. However, there are two additional victory conditions:
Victory conditions Victory condition Definition Emitwe-ebiri during the same move, a player can win by capturing opponent's seeds on both ends of the board. Akakyala in some tournaments, a player may win by capturing in each of two separate moves, before the opponent has captured their first seed. In addition, a special win called akawumbi occurs when a player captures seeds from each of an opponent's pits in one turn. In a tournament, this may be weighted several times a more mundane victory.
Never ending moves
It is possible for a move to lead to a never-ending sowing sequence. In tournament play, a player is allowed up to three minutes to finish his move - if this cannot be done, the game is annulled.
Never ending omweso moves have been of some mathematical interest. The Mayer Test can be used to determine whether a position can lead to a never-ending sowing.
See also
External links
- James S. Coleman, Play in Uganda: Omweso a Game People, UCLA African Studies Center, 1970
- Article on Omweso rules and society in East Africa.
Categories:- Ugandan culture
- Traditional mancala games
Wikimedia Foundation. 2010.

