Equipartition theorem

[
Thermal motion of an α-helical peptide. The jittery motion is random and complex, and the energy of any particular atom can fluctuate wildly. Nevertheless, the equipartition theorem allows the "average" kinetic energy of each atom to be computed, as well as the "average" potential energies of many vibrational modes. The grey, red and blue spheres represent atoms of carbon, oxygen and nitrogen, respectively; the smaller white spheres represent atoms of hydrogen.]

In classical statistical mechanics, the equipartition theorem is a general formula that relates the temperature of a system with its average energies. The equipartition theorem is also known as the law of equipartition, equipartition of energy, or simply equipartition. The original idea of equipartition was that, in thermal equilibrium, energy is shared equally among its various forms; for example, the average kinetic energy in the translational motion of a molecule should equal the average kinetic energy in its rotational motion.

The equipartition theorem makes quantitative predictions. Like the virial theorem, it gives the "total" average kinetic and potential energies for a system at a given temperature, from which the system's heat capacity can be computed. However, equipartition also gives the average values of "individual components" of the energy, such as the kinetic energy of a particular particle or the potential energy of a single spring. For example, it predicts that every molecule in an ideal gas has an average kinetic energy of (3/2)"k_BT" in thermal equilibrium, where "k_B" is the Boltzmann constant and "T" is the temperature. More generally, it can be applied to any classical system in thermal equilibrium, no matter how complicated. The equipartition theorem can be used to derive the classical ideal gas law, and the Dulong–Petit law for the specific heat capacities of solids. It can also be used to predict the properties of stars, even white dwarfs and neutron stars, since it holds even when relativistic effects are considered. Although the equipartition theorem makes very accurate predictions in certain conditions, it becomes inaccurate when quantum effects are significant, namely at low enough temperatures. When the thermal energy "k_BT" is smaller than the quantum energy spacing in a particular degree of freedom, the average energy and heat capacity of this degree of freedom are less than the values predicted by equipartition. Such a degree of freedom is said to be "frozen out" when the thermal energy is much smaller than this spacing. For example, the specific heat of a solid decreases at low temperatures as various types of motion become frozen out, rather than remaining constant as predicted by equipartition. Such decreases in specific heat were the first sign to physicists of the 19th century that classical physics was incorrect and that new physics was needed. Along with other evidence, equipartition's failure for electromagnetic radiation — also known as the ultraviolet catastrophe — led Albert Einstein to suggest that light itself was quantized into photons, a revolutionary hypothesis that spurred the development of quantum mechanics and quantum field theory.

Basic concept and simple examples

[

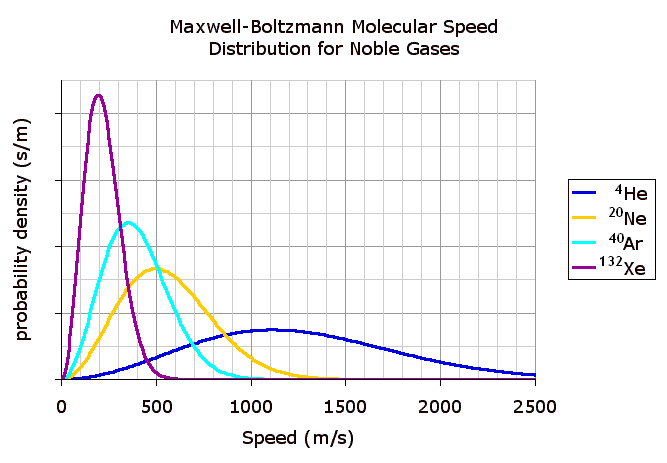
right|thumb|440px|Figure_2._Probability_density_functions_of_the_molecular_speed_for_four_noble gases at a temperature of 298.15 K (25 °C). The four gases are helium (⁴He), neon (²⁰Ne), argon (⁴⁰Ar) and xenon (¹³²Xe); the superscripts indicate their mass numbers. These probability density functions have dimensions of probability times inverse speed; since probability is dimensionless, they can be expressed in units of seconds per meter.]

The name "equipartition" means "share and share alike". The original concept of equipartition was that the total kinetic energy of a system is shared equally among all of its independent parts, "on the average", once the system has reached thermal equilibrium. Equipartition also makes quantitative predictions for these energies. For example, it predicts that every atom of a noble gas, in thermal equilibrium at temperature "T", has an average translational kinetic energy of (3/2)"k_BT", where "k_B" is the Boltzmann constant. As a consequence, the heavier atoms of xenon have a lower average speed than do the lighter atoms of helium at the same temperature. Figure 2 shows the Maxwell–Boltzmann distribution for the speeds of the atoms in four noble gases.

In this example, the key point is that the kinetic energy is quadratic in the velocity. The equipartition theorem shows that in thermal equilibrium, any degree of freedom (such as a component of the position or velocity of a particle) which appears only quadratically in the energy has an average energy of ½"k_BT" and therefore contributes ½"k_B" to the system's heat capacity. This has many applications.

Translational energy and ideal gases

The (Newtonian) kinetic energy of a particle of mass "m", velocity v is given by

: $H^{mathrm{kin = frac12 m |mathbf{v}|^2 = frac{1}{2} mleft( v_{x}^{2} + v_{y}^{2} + v_{z}^{2}
ight),$

where "v_x", "v_y" and "v_z" are the cartesian components of the velocity v. Here, "H" is short for Hamiltonian, and used henceforth as a symbol for energy because the Hamiltonian formalism plays a central role in the most general form of the equipartition theorem.

Since the kinetic energy is quadratic in the components of the velocity, by equipartition these three components each contribute ½"k_BT" to the average kinetic energy in thermal equilibrium. Thus the average kinetic energy of the particle is (3/2)"k_B"T, as in the example of noble gases above.

More generally, in an ideal gas, the total energy consists purely of (translational) kinetic energy: by assumption, the particles have no internal degrees of freedom and move independently of one another. Equipartition therefore predicts that the average total energy of an ideal gas of "N" particles is (3/2) "N k_BT".

It follows that the heat capacity of the gas is (3/2) "N k_B" and hence, in particular, the heat capacity of a mole of a such gas particles is (3/2)"N_Ak_B"=(3/2)"R", where "N_A" is Avogadro's number and "R" is the gas constant. Since "R" ≈ 2 cal/(mol·K), equipartition predicts that the molar heat capacity of an ideal gas is roughly 3 cal/(mol·K). This prediction is confirmed by experiment.

The mean kinetic energy also allows the root mean square speed "v_rms" of the gas particles to be calculated:

: $v_{mathrm{rms = sqrt{langle v^{2}
angle} = sqrt{frac{3 k_{B} T}{m = sqrt{frac{3 R T}{M,$

where "M = N_Am" is the mass of a mole of gas particles. This result is useful for many applications such as Graham's law of effusion, which provides a method for enriching uranium. [ [http://www.nrc.gov/reading-rm/doc-collections/fact-sheets/enrichment.html Fact Sheet on Uranium Enrichment] U.S. Nuclear Regulatory Commission. Accessed 30th April 2007]

Rotational energy and molecular tumbling in solution

A similar example is provided by a rotating molecule with principal moments of inertia "I₁", "I₂" and "I₃". The rotational energy of such a molecule is given by

: $H^{mathrm{rot = frac{1}{2} ( I_{1} omega_{1}^{2} + I_{2} omega_{2}^{2} + I_{3} omega_{3}^{2} ),$ where "ω₁", "ω₂", and "ω₃" are the principal components of the angular velocity. By exactly the same reasoning as in the translational case, equipartition implies that in thermal equilibrium the average rotational energy of each particle is (3/2)"k_BT". Similarly, the equipartition theorem allows the average (more precisely, the root mean square) angular speed of the molecules to be calculated.

The tumbling of rigid molecules — that is, the random rotations of molecules in solution — plays a key role in the relaxations observed by nuclear magnetic resonance, particularly protein NMR and residual dipolar couplings. [ Bigr angle = delta_{mn} k_{B} T.

Here "δ_mn" is the Kronecker delta, which is equal to one if "m"="n" and is zero otherwise. The averaging brackets $leftlangle ldots
ight
angle$ is assumed to be an ensemble average over phase space or, under an assumption of ergodicity, a time average of a single system.

: $H^{mathrm{grav_{mathrm{tot = -int_{0}^{R} frac{4pi r^{2} G}{r} M(r),
ho(r), dr,$

where "M(r)" is the mass within a radius "r" and "ρ(r)" is the stellar density at radius "r"; "G" represents the gravitational constant and "R" the total radius of the star. Assuming a constant density throughout the star, this integration yields the formula

: $H^{mathrm{grav_{mathrm{tot = - frac{3G M^{2{5R},$

where "M" is the star's total mass. Hence, the average potential energy of a single particle is

: $langle H^{mathrm{grav
angle = frac{H^{mathrm{grav_{mathrm{tot}{N} = - frac{3G M^{2{5RN},$

where "N" is the number of particles in the star. Since most stars are composed mainly of ionized hydrogen, "N" equals roughly "(M/m_p)", where "m_p" is the mass of one proton. Application of the equipartition theorem gives an estimate of the star's temperature

: $Bigllangle r frac{partial H^{mathrm{grav}{partial r} Bigr
angle = langle -H^{mathrm{grav
angle = k_{B} T = frac{3G M^{2{5RN}.$

Substitution of the mass and radius of the Sun yields an estimated solar temperature of "T" = 14 million kelvins, very close to its core temperature of 15 million kelvins. However, the Sun is much more complex than assumed by this model — both its temperature and density vary strongly with radius — and such excellent agreement (≈7% relative error) is partly fortuitous. [cite book | last = Noyes | first = RW | year = 1982 | title = The Sun, Our Star | publisher = Harvard University Press | location = Cambridge, MA | id = ISBN 0-674-85435-7]

tar formation

The same formulae may be applied to determining the conditions for star formation in giant molecular clouds. [cite book | last = Ostlie | first = DA | coauthors = Carroll BW | year = 1996 | title = An Introduction to Modern Stellar Astrophysics | publisher = Addison-Wesley | location = Reading, MA | id = ISBN 0-201-59880-9] A local fluctuation in the density of such a cloud can lead to a runaway condition in which the cloud collapses inwards under its own gravity. Such a collapse occurs when the equipartition theorem — or, equivalently, the virial theorem — is no longer valid, i.e., when the gravitational potential energy exceeds twice the kinetic energy

: $frac{3G M^{2{5R} > 3 N k_{B} T$

Assuming a constant density ρ for the cloud

: $M = frac{4}{3} pi R^{3}
ho$

yields a minimum mass for stellar contraction, the Jeans mass "M_J"

: $M_{J}^{2} = left( frac{5k_{B}T}{G m_{p
ight)^{3} left( frac{3}{4pi
ho}
ight)$

Substituting the values typically observed in such clouds ("T"=150 K, ρ = 2×10^-16 g/cm³) gives an estimated minimum mass of 17 solar masses, which is consistent with observed star formation. This effect is also known as the Jeans instability, after the British physicist James Hopwood Jeans who published it in 1902. [cite journal | last = Jeans | first = JH | authorlink = James Hopwood Jeans | year = 1902 | title = The Stability of a Spherical Nebula | journal = Phil.Trans. A | volume = 199 | pages = 1–53 | doi = 10.1098/rsta.1902.0012]

Derivations

Kinetic energies and the Maxwell–Boltzmann distribution

The original formulation of the equipartition theorem states that, in any physical system in thermal equilibrium, every particle has exactly the same average kinetic energy, (3/2)"k_BT".cite book | last = McQuarrie | first = DA | year = 2000 | title = Statistical Mechanics | edition = revised 2nd ed. | publisher = University Science Books | id = ISBN 978-1891389153 | pages = pp. 121–128] This may be shown using the Maxwell–Boltzmann distribution (see Figure 2), which is the probability distribution

: $f (v) = 4 pi left( frac{m}{2 pi k_B T}
ight)^{3/2}!!v^2exp Bigl(frac{-mv^2}{2k_B T}Bigr)$

for the speed of a particle of mass "m" in the system, where the speed "v" is the magnitude $sqrt{v_x^2 + v_y^2 + v_z^2}$ of the velocity vector $mathbf{v} = (v_x,v_y,v_z)$ .

The Maxwell–Boltzmann distribution applies to any system composed of atoms, and assumes only a canonical ensemble, specifically, that the kinetic energies are distributed according to their Boltzmann factor at a temperature "T". The average kinetic energy for a particle of mass "m" is then given by the integral formula

: $langle H^{mathrm{kin
angle = langle frac{1}{2} m v^{2}
angle = int _{0}^{infty} frac{1}{2} m v^{2} f(v) dv = frac{3}{2} k_{B} T,$

as stated by the equipartition theorem.The same result can also be obtained by averaging the particle energyusing the probability of finding the particle in certain quantum energy state.

Quadratic energies and the partition function

More generally, the equipartition theorem states that any degree of freedom "x" which appears in the total energy "H" only as a simple quadratic term "Ax"², where "A" is a constant, has an average energy of "½k_BT" in thermal equilibrium. In this case the equipartition theorem may be derived from the partition function "Z"("β"), where "β"=1/("k"_"B""T") is the canonical inverse temperature. [cite book | last = Callen | first = HB | authorlink = Herbert Callen | year = 1985 | title = Thermodynamics and an Introduction to Thermostatistics | publisher = John Wiley and Sons | location = New York | pages = pp. 375–377 | id = ISBN 0-471-86256-8] Integration over the variable "x" yields a factor

: $Z_{x} = int_{-infty}^{infty} dx e^{-eta A x^{2 = sqrt{frac{pi}{eta A,$

in the formula for "Z". The mean energy associated with this factor is given by

: $langle H_{x}
angle = - frac{partial log Z_{x{partial eta} = frac{1}{2eta} = frac{1}{2} k_{B} T$

as stated by the equipartition theorem.

General proofs

General derivations of the equipartition theorem can be found in many statistical mechanics textbooks, both for the microcanonical ensemble and for the canonical ensemble.They involve taking averages over the phase space of the system, which is a symplectic manifold.

To explain these derivations, the following notation is introduced. First, the phase space is described in terms of generalized position coordinates "q"_"j" together with their conjugate momenta "p"_"j". The quantities "q"_"j" completely describe the configuration of the system, while the quantities ("q"_"j","p"_"j") together completely describe its state.

Secondly, the infinitesimal volume: $dGamma = prod_{i} dq_{i} dp_{i}$ of the phase space is introduced and used to define the volume Γ("E", Δ"E") of the portion of phase space where the energy "H" of the system lies between two limits, "E" and "E+ΔE":

: $Gamma (E, Delta E) = int_{H in left [E, E+Delta E
ight] } dGamma .$ In this expression, "ΔE" is assumed to be very small, "ΔE<: $Sigma (E) = int_{H < E} dGamma .$

Since "ΔE" is very small, the following integrations are equivalent

: $int_{H in left [ E, E+Delta E
ight] } ldots dGamma = Delta E frac{partial}{partial E} int_{H < E} ldots dGamma,$

where the ellipses represent the integrand. From this, it follows that Γ is proportional to ΔE

: $Gamma = Delta E frac{partial Sigma}{partial E} = Delta E
ho(E),$

where "ρ(E)" is the density of states. By the usual definitions of statistical mechanics, the entropy "S" equals "k_B" log "Σ(E)", and the temperature "T" is defined by

: $frac{1}{T} = frac{partial S}{partial E} = k_{b} frac{partial log Sigma}{partial E} = k_{b} frac{1}{Sigma},frac{partial Sigma}{partial E} .$

The canonical ensemble

In the canonical ensemble, the system is in thermal equilibrium with an infinite heat bath at temperature "T" (in Kelvin). The probability of each state in phase space is given by its Boltzmann factor times a normalization factor $mathcal{N}$ , which is chosen so that the probabilities sum to one

: $mathcal{N} int e^{-eta H(p, q)} dGamma = 1,$

where "β = 1/k_BT". Integration by parts for a phase-space variable "x_k" (which could be either "q_k" or "p_k") between two limits "a" and "b" yields the equation

: $mathcal{N} int left [ e^{-eta H(p, q)} x_{k}
ight] _{x_{k}=a}^{x_{k}=b} dGamma_{k}+ mathcal{N} int e^{-eta H(p, q)} x_{k} eta frac{partial H}{partial x_{k dGamma = 1,$

where "dΓ_k = dΓ/dx_k", i.e., the first integration is not carried out over "x_k". The first term is usually zero, either because "x_k" is zero at the limits, or because the energy goes to infinity at those limits. In that case, the equipartition theorem for the canonical ensemble follows immediately

: $mathcal{N} int e^{-eta H(p, q)} x_{k} frac{partial H}{partial x_{k ,dGamma = Bigllangle x_{k} frac{partial H}{partial x_{k Bigr
angle = frac{1}{eta} = k_{B} T.$

Here, the averaging symbolized by $langle ldots
angle$ is the ensemble average taken over the canonical ensemble.

The microcanonical ensemble

In the microcanonical ensemble, the system is isolated from the rest of the world, or at least very weakly coupled to it. Hence, its total energy is effectively constant; to be definite, we say that the total energy "H" is confined between "E" and "E+ΔE". For a given energy "E" and spread "ΔE", there is a region of phase space Γ in which the system has that energy, and the probability of each state in that region of phase space is equal, by the definition of the microcanonical ensemble. Given these definitions, the equipartition average of phase-space variables "x_m" (which could be either "q_k"or "p_k") and "x_n" is given by

: $egin{align}Bigllangle x_{m} frac{partial H}{partial x_{n Bigr
angle &=frac{1}{Gamma} , int_{H in left [ E, E+Delta E
ight] } x_{m} frac{partial H}{partial x_{n ,dGamma\\&=frac{Delta E}{Gamma}, frac{partial}{partial E} int_{H < E} x_{m} frac{partial H}{partial x_{n ,dGamma\\&= frac{1}{
ho} ,frac{partial}{partial E} int_{H < E} x_{m} frac{partial left( H - E
ight)}{partial x_{n ,dGamma,end{align}$

where the last equality follows because "E" is a constant that does not depend on "x_n". Integrating by parts yields the relation

: $egin{align}int_{H < E} x_{m} frac{partial ( H - E )}{partial x_{n ,dGamma &= int_{H < E} frac{partial}{partial x_{n igl( x_{m} ( H - E ) igr) ,dGamma - int_{H < E} delta_{mn} ( H - E ) dGamma\\&= delta_{mn} int_{H < E} ( E - H ) ,dGamma,end{align}$ since the first term on the right hand side of the first line is zero (it can be rewritten as an integral of "H" - "E" on the hypersurface where "H" = "E").

Substitution of this result into the previous equation yields

: $Bigllangle x_{m} frac{partial H}{partial x_{n Bigr
angle = delta_{mn} frac{1}{
ho} , frac{partial}{partial E} int_{H < E}left( E - H
ight),dGamma = delta_{mn} frac{1}{
ho} , int_{H < E} ,dGamma = delta_{mn} frac{Sigma}{
ho}.$

Since $ho = frac{partial Sigma}{partial E}$ the equipartition theorem follows:

: $Bigllangle x_{m} frac{partial H}{partial x_{n Bigr
angle = delta_{mn} Bigl(frac{1}{Sigma} frac{partial Sigma}{partial E}Bigr)^{-1} = delta_{mn} Bigl(frac{partial log Sigma} {partial E}Bigr)^{-1} = delta_{mn} k_{B} T.$

Thus, we have derived the general formulation of the equipartition theorem

: $!Bigllangle x_{m} frac{partial H}{partial x_{n Bigr
angle = delta_{mn} k_{B} T,$

which was so useful in the applications described above.

Limitations

[
normal modes in an isolated system of ideal coupled oscillators; the energy in each mode is constant and independent of the energy in the other modes. Hence, the equipartition theorem does "not" hold for such a system in the microcanonical ensemble (when isolated), although it does hold in the canonical ensemble (when coupled to a heat bath). However, by adding a sufficiently strong nonlinear coupling between the modes, energy will be shared and equipartition holds in both ensembles.]

Requirement of ergodicity

The law of equipartition holds only for ergodic systems in thermal equilibrium, which implies that all states with the same energy must be equally likely to be populated. Consequently, it must be possible to exchange energy among all its various forms within the system, or with an external heat bath in the canonical ensemble. The number of physical systems that have been rigorously proven to be ergodic is small; a famous example is the hard-sphere system of Yakov Sinai. [cite book | last = Arnold | first = VI | authorlink = Vladimir Arnold | coauthors = Avez A | year = 1967 | title = Théorie ergodique des systèms dynamiques | publisher = Gauthier-Villars, Paris. fr icon (English edition: Benjamin-Cummings, Reading, Mass. 1968)] The requirements for isolated systems to ensure ergodicity — and, thus equipartition — have been studied, and provided motivation for the modern chaos theory of dynamical systems. A chaotic Hamiltonian system need not be ergodic, although that is usually a good assumption.

A commonly cited counter-example where energy is "not" shared among its various forms and where equipartition does "not" hold in the microcanonical ensemble is a system of coupled harmonic oscillators.cite book | last = Reichl | first = LE | year = 1998 | title = A Modern Course in Statistical Physics | edition = 2nd ed. | publisher = Wiley Interscience | id = ISBN 978-0471595205 | pages = 326–333] If the system is isolated from the rest of the world, the energy in each normal mode is constant; energy is not transferred from one mode to another. Hence, equipartition does not hold for such a system; the amount of energy in each normal mode is fixed at its initial value. If sufficiently strong nonlinear terms are present in the energy function, energy may be transferred between the normal modes, leading to ergodicity and rendering the law of equipartition valid. However, the Kolmogorov–Arnold–Moser theorem states that energy will not be exchanged unless the nonlinear perturbations are strong enough; if they are too small, the energy will remain trapped in at least some of the modes.

Failure due to quantum effects

The law of equipartition breaks down when the thermal energy "k_BT" is significantly smaller than the spacing between energy levels. Equipartition no longer holds because it is a poor approximation to assume that the energy levels form a smooth continuum, which is required in the derivations of the equipartition theorem above. Historically, the failures of the classical equipartition theorem to explain specific heats and blackbody radiation were critical in showing the need for a new theory of matter and radiation, namely, quantum mechanics and quantum field theory.

To illustrate the breakdown of equipartition, consider the average energy in a single (quantum) harmonic oscillator, which was discussed above for the classical case. Its quantum energy levels are given by "E_n = nhν", where "h" is Planck's constant, "ν" is the fundamental frequency of the oscillator, and "n" is an integer. The probability of a given energy level being populated in the canonical ensemble is given by its Boltzmann factor

: $P(E_{n}) = frac{e^{-neta h
u{Z},$

where "β" = 1/"k"_"B""T" and the denominator "Z" is the partition function, here a geometric series

: $Z = sum_{n=0}^{infty} e^{-neta h
u} = frac{1}{1 - e^{-eta h
u.$

Its average energy is given by

: $langle H
angle = sum_{n=0}^{infty} E_{n} P(E_{n}) =frac{1}{Z} sum_{n=0}^{infty} nh
u e^{-neta h
u} = -frac{1}{Z} frac{partial Z}{partial eta} = -frac{partial log Z}{partial eta}.$

Substituting the formula for "Z" gives the final result

: $langle H
angle = h
u frac{e^{-eta h
u{1 - e^{-eta h
u.$

At high temperatures, when the thermal energy "k_BT" is much greater than the spacing "hν" between energy levels, the exponential argument "βhν" is much less than one and the average energy becomes "k_BT", in agreement with the equipartition theorem (Figure 10). However, at low temperatures, when "hν" >> "k_BT", the average energy goes to zero — the higher-frequency energy levels are "frozen out" (Figure 10). As another example, the internal excited electronic states of a hydrogen atom do not contribute to its specific heat as a gas at room temperature, since the thermal energy "k_BT" (roughly 0.025 eV) is much smaller than the spacing between the lowest and next higher electronic energy levels (roughly 10 eV).

Similar considerations apply whenever the energy level spacing is much larger than the thermal energy. For example, this reasoning was used by Albert Einstein to resolve the ultraviolet catastrophe of blackbody radiation.cite journal | last = Einstein | first = A | authorlink = Albert Einstein | year = 1905 | title = Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt (A Heuristic Model of the Creation and Transformation of Light) | journal = Annalen der Physik | volume = 17 | pages = 132–148 | url = http://gallica.bnf.fr/ark:/12148/CadresFenetre?O=NUMM-209459&M=chemindefer | doi = 10.1002/andp.19053220607 de icon. An is available from Wikisource.] The paradox arises because there are an infinite number of independent modes of the electromagnetic field in a closed container, each of which may be treated as a harmonic oscillator. If each electromagnetic mode were to have an average energy "k_BT", there would be an infinite amount of energy in the container. [cite journal | last = Rayleigh | first = JWS | authorlink = John Strutt, 3rd Baron Rayleigh | year = 1900 | title = Remarks upon the Law of Complete Radiation | journal = Philosophical Magazine | volume = 49 | pages = 539–540] However, by the reasoning above, the average energy in the higher-ω modes goes to zero as ω goes to infinity; moreover, Planck's law of black body radiation, which describes the experimental distribution of energy in the modes, follows from the same reasoning.

Other, more subtle quantum effects can lead to corrections to equipartition, such as identical particles and continuous symmetries. The effects of identical particles can be dominant at very high densities and low temperatures. For example, the valence electrons in a metal can have a mean kinetic energy of a few electronvolts, which would normally correspond to a temperature of tens of thousands of kelvins. Such a state, in which the density is high enough that the Pauli exclusion principle invalidates the classical approach, is called a degenerate fermion gas. Such gases are important for the structure of white dwarf and nuetron stars. At low temperatures, a fermionic analogue of the Bose–Einstein condensate (in which a large number of identical particles occupy the lowest-energy state) can form; such superfluid electrons are responsible for superconductivity.

ee also

* Virial theorem
* Kinetic theory
* Statistical mechanics
* Quantum statistical mechanics

Notes and references

Further reading

* ASIN B00085D6OO

External links

* [http://webphysics.davidson.edu/physlet_resources/thermo_paper/thermo/examples/ex20_4.html Applet demonstrating equipartition in real time for a mixture of monatomic and diatomic gases]
* [http://www.sciencebits.com/StellarEquipartition The equipartition theorem in stellar physics] , written by Nir J. Shaviv, an associate professor at the Racah Institute of Physics in the Hebrew University of Jerusalem.

Wikimedia Foundation. 2010.

Игры ⚽ Поможем написать курсовую

Look at other dictionaries:

Equipartition de l'énergie — Équipartition de l énergie Agitation thermique d’un peptide avec une structure en hélice alpha. Les mouvements sont aléatoires et complexes, l’énergie d’un atome peut fluctuer énormément. Néanmoins, le théorème d’équipartition permet de calculer… … Wikipédia en Français
Équipartition de l'énergie — Agitation thermique d’un peptide avec une structure en hélice alpha. Les mouvements sont aléatoires et complexes, l’énergie d’un atome peut fluctuer énormément. Néanmoins, le théorème d’équipartition permet de calculer l’énergie cinétique moyenne … Wikipédia en Français
Theoreme d'equipartition — Équipartition de l énergie Agitation thermique d’un peptide avec une structure en hélice alpha. Les mouvements sont aléatoires et complexes, l’énergie d’un atome peut fluctuer énormément. Néanmoins, le théorème d’équipartition permet de calculer… … Wikipédia en Français
Théorème d'équipartition — Équipartition de l énergie Agitation thermique d’un peptide avec une structure en hélice alpha. Les mouvements sont aléatoires et complexes, l’énergie d’un atome peut fluctuer énormément. Néanmoins, le théorème d’équipartition permet de calculer… … Wikipédia en Français
Théorème d’équipartition — Équipartition de l énergie Agitation thermique d’un peptide avec une structure en hélice alpha. Les mouvements sont aléatoires et complexes, l’énergie d’un atome peut fluctuer énormément. Néanmoins, le théorème d’équipartition permet de calculer… … Wikipédia en Français
equipartition of energy — /ee kweuh pahr tish euhn, ek weuh , ee kweuh , ek weuh/, Thermodynamics. the theorem that the kinetic energy is the same for each degree of freedom in a system in thermal equilibrium. [1900 05; EQUI + PARTITION] * * * … Universalium
equipartition of energy — an ideal condition postulated as existing among the molecules, atoms, and ions of a gas or vapor wherein the total heat energy is equally apportioned among the various degrees of freedom possessed by those particles, the realization of this ideal … Useful english dictionary
Virial theorem — In mechanics, the virial theorem provides a general equation relating the average over time of the total kinetic energy, , of a stable system consisting of N particles, bound by potential forces, with that of the total potential energy, , where… … Wikipedia
Fluctuation dissipation theorem — In statistical physics, the fluctuation dissipation theorem is a powerful tool for predicting the non equilibrium behavior of a system such as the irreversible dissipation of energy into heat from its reversible fluctuations in thermal… … Wikipedia
Noisy-channel coding theorem — In information theory, the noisy channel coding theorem (sometimes Shannon s theorem), establishes that for any given degree of noise contamination of a communication channel, it is possible to communicate discrete data (digital information)… … Wikipedia

Academic Dictionaries and Encyclopedias

Equipartition theorem

Look at other dictionaries:

Share the article and excerpts

Academic Dictionaries and Encyclopedias

Wikipedia

Equipartition theorem

Look at other dictionaries:

Share the article and excerpts

Direct link