Degrees of freedom (physics and chemistry)

A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system. The set of all dimensions of a system is known as a phase space.

Definition

In physics, a degree of freedom of a system is a formal description of a parameter that contributes to the state of a physical system.

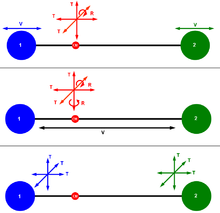
In mechanics, a point particle can move independently in the three directions of space. Thus, the momentum of a particle consists of three components, each called a degree of freedom. A system of N independent particles, therefore, has the total of 3N degrees of freedom.

Similarly in statistical mechanics, a degree of freedom is a single scalar number describing the microstate of a system. The specification of all microstates of a system is a point in the system's phase space.

A degree of freedom may be any useful property that is not dependent on other variables. For example, in the 3D ideal chain model, two angles are necessary to describe each monomer's orientation.

Example: diatomic gas

Different ways of visualizing the 3 degrees of freedom of a dumbbell-shaped diatomic molecule. (CM: center of mass of the system, T: translational motion, R: rotational motion, V: vibrational motion.)

In three-dimensional space, three degrees of freedom are associated with the movement of a mechanical particle. A diatomic gas molecule thus has 6 degrees of freedom. This set may be decomposed in terms of translations, rotations, and vibrations of the molecule. The center of mass motion of the entire molecule accounts for 3 degrees of freedom. In addition, the molecule has one vibrational mode and two rotational degrees of motion. The rotations occur around the two axes perpendicular to the line between the two atoms. The rotation around the atom-atom bond is not counted. This yields, for a diatomic molecule, a decomposition of:

3N = 6 = 3+1+2.

For a general molecule with N > 2 atoms, all 3 rotational degrees of freedom are considered, resulting in the decomposition:

3 N = 3 + 3 + (3 N - 6)

which means that an N-atom molecule has 3N - 6 vibrational degrees of freedom for N > 2.

Contrary to the classical equipartition theorem, at room temperature, the vibrational motion of molecules typically makes negligible contributions to the heat capacity. This is because these degrees of freedom are frozen because the spacing between the energy eigenvalues exceeds the energy corresponding to ambient temperatures (kT). In the following table such degrees of freedom are disregarded because of their low effect on total energy. However, at very high temperatures they cannot be neglected.

	Monatomic	Linear molecules	Non-Linear molecules
Position (x, y and z)	3	3	3
Rotation (x, y and z)	0	2	3
Vibration	0	3N - 5	3N - 6
Total	3	3N	3N

Independent degrees of freedom

The set of degrees of freedom $X_1, \ldots, X_N$ of a system is independent if the energy associated with the set can be written in the following form:

$E = \sum_{i=1}^N E_i(X_i),$

where E_i is a function of the sole variable X_i.

example: if X₁ and X₂ are two degrees of freedom, and E is the associated energy:

• If $E = X_1^4 + X_2^4$, then the two degrees of freedom are independent.
• If $E = X_1^4 + X_1 X_2 + X_2^4$, then the two degrees of freedom are not independent. The term involving the product of X₁ and X₂ is a coupling term, that describes an interaction between the two degrees of freedom.

At thermodynamic equilibrium, $X_1, \ldots, X_n$ are all statistically independent of each other.

For i from 1 to N, the value of the ith degree of freedom X_i is distributed according to the Boltzmann distribution. Its probability density function is the following:

$p_i(X_i) = \frac{e^{-\frac{E_i}{k_B T}}}{\int dX_i \, e^{-\frac{E_i}{k_B T}}}$,

In this section, and throughout the article the brackets $\langle \rangle$ denote the mean of the quantity they enclose.

The internal energy of the system is the sum of the average energies associated to each of the degrees of freedom:

$\langle E \rangle = \sum_{i=1}^N \langle E_i \rangle.$

Demonstrations

A system exchanges energy in the form of heat with its surroundings and the number of particles in the system remains fixed. This corresponds to studying the system in the canonical ensemble. Note that in statistical mechanics, a result that is demonstrated for a system in a particular ensemble remains true for this system at the thermodynamic limit in any ensemble. In the canonical ensemble, at thermodynamic equilibrium, the state of the system is distributed among all micro-states according to the Boltzmann distribution. If T is the system's temperature and k_B is Boltzmann's constant, then the probability density function associated to each micro-state is the following:

$P(X_1, \ldots, X_N) = \frac{e^{-\frac{E}{k_B T}}}{\int dX_1\,dX_2 \ldots dX_N e^{-\frac{E}{k_B T}}}$,

The denominator in the above expression plays an important role.^[1] This expression immediately breaks down into a product of terms depending of a single degree of freedom:

$P(X_1, \ldots, X_N) = p_1(X_1) \ldots p_N(X_N)$

The existence of such a breakdown of the multidimensional probability density function into a product of functions of one variable is enough by itself to demonstrate that $X_1 \ldots X_N$ are statistically independent from each other.

Since each function p_i is normalized, it follows immediately that p_i is the probability density function of the degree of freedom X_i, for i from 1 to N.

Finally, the internal energy of the system is its mean energy. The energy of a degree of freedom E_i is a function of the sole variable X_i. Since $X_1, \ldots, X_N$ are independent from each other, the energies $E_1(X_1), \ldots, E_N(X_N)$ are also statistically independent from each other. The total internal energy of the system can thus be written as:

$U = \langle E \rangle = \langle \sum_{i=1}^N E_i \rangle = \sum_{i=1}^N \langle E_i \rangle$

Quadratic degrees of freedom

A degree of freedom X_i is quadratic if the energy terms associated to this degree of freedom can be written as

$E = \alpha_i\,\,X_i^2 + \beta_i \,\, X_i Y$,

where Y is a linear combination of other quadratic degrees of freedom.

example: if X₁ and X₂ are two degrees of freedom, and E is the associated energy:

• If $E = X_1^4 + X_1^3 X_2 + X_2^4$, then the two degrees of freedom are not independent and non-quadratic.
• If $E = X_1^4 + X_2^4$, then the two degrees of freedom are independent and non-quadratic.
• If $E = X_1^2 + X_1 X_2 + 2X_2^2$, then the two degrees of freedom are not independent but are quadratic.
• If $E = X_1^2 + 2X_2^2$, then the two degrees of freedom are independent and quadratic.

For example, in Newtonian mechanics, the dynamics of a system of quadratic degrees of freedom are controlled by a set of homogeneous linear differential equations with constant coefficients.

Quadratic and independent degree of freedom

$X_1, \ldots, X_N$ are quadratic and independent degrees of freedom if the energy associated to a microstate of the system they represent can be written as:

$E = \sum_{i=1}^N \alpha_i X_i^2$

Equipartition theorem

In the classical limit of statistical mechanics, at thermodynamic equilibrium, the internal energy of a system of N quadratic and independent degrees of freedom is:

$U = \langle E \rangle = N\,\frac{k_B T}{2}$

Here, the mean energy associated with a degree of freedom is:

$\langle E_i \rangle = \int dX_i\,\,\alpha_i X_i^2\,\, p_i(X_i) = \frac{\int dX_i\,\,\alpha_i X_i^2\,\, e^{-\frac{\alpha_i X_i^2}{k_B T}}}{\int dX_i\,\, e^{-\frac{\alpha_i X_i^2}{k_B T}}}$

$\langle E_i \rangle = \frac{k_B T}{2}\frac{\int dx\,\,x^2\,\, e^{-\frac{x^2}{2}}}{\int dx\,\, e^{-\frac{x^2}{2}}} = \frac{k_B T}{2}$

Since the degrees of freedom are independent, the internal energy of the system is equal to the sum of the mean energy associated with each degree of freedom, which demonstrates the result.

References

1. ^ "Configuration integral (statistical mechanics)". http://clesm.mae.ufl.edu/wiki.pub/index.php/Configuration_integral_%28statistical_mechanics%29#Thermodynamic_properties.