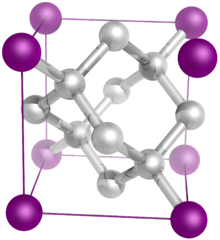
Crystal system

Diamond crystal structure consists of face-centered cubic lattice.

In crystallography, the terms crystal system, crystal family, and lattice system each refer to one of several classes of space groups, lattices, point groups, or crystals. Informally, two crystals tend to be in the same crystal system if they have similar symmetries, though there are many exceptions to this.

Crystal systems, crystal families, and lattice systems are similar but slightly different, and there is widespread confusion between them: in particular the trigonal crystal system is often confused with the rhombohedral lattice system, and the term "crystal system" is sometimes used to mean "lattice system" or "crystal family".

Space groups and crystals are divided into 7 crystal systems according to their point groups, and into 7 lattice systems according to their Bravais lattices. Five of the crystal systems are essentially the same as five of the lattice systems, but the hexagonal and trigonal crystal systems differ from the hexagonal and rhombohedral lattice systems. The six crystal families are formed by combining the hexagonal and trigonal crystal systems into one hexagonal family, in order to eliminate this confusion.

Overview

Hexagonal Hanksite crystal, with three-fold c-axis symmetry

A lattice system is a class of lattices with the same point group. In three dimensions there are seven lattice systems: triclinic, monoclinic, orthorhombic, tetragonal, rhombohedral, hexagonal, and cubic. The lattice system of a crystal or space group is determined by its lattice but not always by its point group.

A crystal system is a class of point groups. Two point groups are placed in the same crystal system if the sets of possible lattice systems of their space groups are the same. For many point groups there is only one possible lattice system, and in these cases the crystal system corresponds to a lattice system and is given the same name. However, for the five point groups in the trigonal crystal class there are two possible lattice systems for their point groups: rhombohedral or hexagonal. In three dimensions there are seven crystal systems: triclinic, monoclinic, orthorhombic, tetragonal, trigonal, hexagonal, and cubic. The crystal system of a crystal or space group is determined by its point group but not always by its lattice.

A crystal family also consists of point groups and is formed by combining crystal systems whenever two crystal systems have space groups with the same lattice. In three dimensions a crystal family is almost the same as a crystal system (or lattice system), except that the hexagonal and trigonal crystal systems are combined into one hexagonal family. In three dimensions there are six crystal families: triclinic, monoclinic, orthorhombic, tetragonal, hexagonal, and cubic. The crystal family of a crystal or space group is determined by either its point group or its lattice, and crystal families are the smallest collections of point groups with this property.

In dimensions less than three there is no essential difference between crystal systems, crystal families, and lattice systems. There are 1 in dimension 0, 1 in dimension 1, and 4 in dimension 2, called oblique, rectangular, square, and hexagonal.

The relation between three-dimensional crystal families, crystal systems, and lattice systems is shown in the following table:

Crystal family	Crystal system	Required symmetries of point group	point groups	space groups	bravais lattices	Lattice system
Triclinic		None	2	2	1	Triclinic
Monoclinic		1 twofold axis of rotation or 1 mirror plane	3	13	2	Monoclinic
Orthorhombic		3 twofold axes of rotation or 1 twofold axis of rotation and two mirror planes.	3	59	4	Orthorhombic
Tetragonal		1 fourfold axis of rotation	7	68	2	Tetragonal
Hexagonal	Trigonal	1 threefold axis of rotation	5	7	1	Rhombohedral
				18	1	Hexagonal
	Hexagonal	1 sixfold axis of rotation	7	27
Cubic		4 threefold axes of rotation	5	36	3	Cubic
Total: 6	7		32	230	14	7

Crystal systems

The distribution of the 32 point groups into the 7 crystal systems is given in the following table.

crystal family	crystal system	point group / crystal class	Schönflies	Hermann-Mauguin	Orbifold	Coxeter	Type	order	structure
triclinic		triclinic-pedial	C1	1	11	[ ]+	enantiomorphic polar	1	trivial
		triclinic-pinacoidal	Ci	1	1x	[2,1+]	centrosymmetric	2	cyclic
monoclinic		monoclinic-sphenoidal	C2	2	22	[2,2]+	enantiomorphic polar	2	cyclic
		monoclinic-domatic	Cs	m	*11	[ ]	polar	2	cyclic
		monoclinic-prismatic	C2h	2/m	2*	[2,2+]	centrosymmetric	4	2×cyclic
orthorhombic		orthorhombic-sphenoidal	D2	222	222	[2,2]+	enantiomorphic	4	dihedral
		orthorhombic-pyramidal	C2v	mm2	*22	[2]	polar	4	dihedral
		orthorhombic-bipyramidal	D2h	mmm	*222	[2,2]	centrosymmetric	8	2×dihedral
tetragonal		tetragonal-pyramidal	C4	4	44	[4]+	enantiomorphic polar	4	Cyclic
		tetragonal-disphenoidal	S4	4	2x	[2+,2]		4	cyclic
		tetragonal-dipyramidal	C4h	4/m	4*	[2,4+]	centrosymmetric	8	2×cyclic
		tetragonal-trapezoidal	D4	422	422	[2,4]+	enantiomorphic	8	dihedral
		ditetragonal-pyramidal	C4v	4mm	*44	[4]	polar	8	dihedral
		tetragonal-scalenoidal	D2d	42m or 4m2	2*2	[2+,4]		8	dihedral
		ditetragonal-dipyramidal	D4h	4/mmm	*422	[2,4]	centrosymmetric	16	2×dihedral
hexagonal	trigonal	trigonal-pyramidal	C3	3	33	[3]+	enantiomorphic polar	3	cyclic
		rhombohedral	S6 (C3i)	3	3x	[2+,3+]	centrosymmetric	6	cyclic
		trigonal-trapezoidal	D3	32 or 321 or 312	322	[3,2]+	enantiomorphic	6	dihedral
		ditrigonal-pyramidal	C3v	3m or 3m1 or 31m	*33	[3]	polar	6	dihedral
		ditrigonal-scalahedral	D3d	3m or 3m1 or 31m	2*3	[2+,6]	centrosymmetric	12	dihedral
	hexagonal	hexagonal-pyramidal	C6	6	66	[6]+	enantiomorphic polar	6	cyclic
		trigonal-dipyramidal	C3h	6	3*	[2,3+]		6	cyclic
		hexagonal-dipyramidal	C6h	6/m	6*	[2,6+]	centrosymmetric	12	2×cyclic
		hexagonal-trapezoidal	D6	622	622	[2,6]+	enantiomorphic	12	dihedral
		dihexagonal-pyramidal	C6v	6mm	*66	[6]	polar	12	dihedral
		ditrigonal-dipyramidal	D3h	6m2 or 62m	*322	[2,3]		12	dihedral
		dihexagonal-dipyramidal	D6h	6/mmm	*622	[2,6]	centrosymmetric	24	2×dihedral
cubic		tetrahedral	T	23	332	[3,3]+	enantiomorphic	12	Alternating
		tetrahedral	Td	43m	*332	[3,3]		24	symmetric
		diploidal	Th	m3	3*2	[3+,4]	centrosymmetric	24	2×alternating
		gyroidal	O	432	432	[4,3]+	enantiomorphic	24	symmetric
		hexoctahedral	Oh	m3m	*432	[4,3]	centrosymmetric	48	2×symmetric

The crystal structures of biological molecules (such as protein structures) can only occur in the 11 enantiomorphic point groups, as biological molecules are invariably chiral. The protein assemblies themselves may have symmetries other than those given above, because they are not intrinsically restricted by the Crystallographic restriction theorem. For example the Rad52 DNA binding protein has an 11-fold rotational symmetry (in human), however, it must form crystals in one of the 11 enantiomorphic point groups given above.

Lattice systems

The distribution of the 14 Bravais lattice types into 7 lattice systems is given in the following table.

The 7 lattice systems	The 14 Bravais Lattices
triclinic (parallelepiped)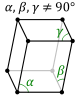
monoclinic (right prism with parallelogram base; here seen from above)	simple	base-centered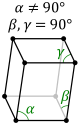
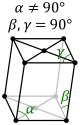
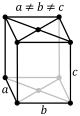
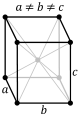
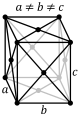
orthorhombic (cuboid)	simple	base-centered	body-centered	face-centered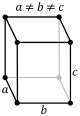
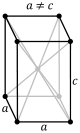
tetragonal (square cuboid)	simple	body-centered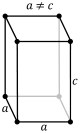
rhombohedral (trigonal trapezohedron)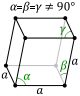
hexagonal (centered regular hexagon)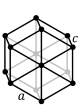
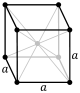
cubic (isometric; cube)	simple	body-centered	face-centered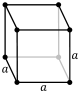

In geometry and crystallography, a Bravais lattice is a category of symmetry groups for translational symmetry in three directions, or correspondingly, a category of translation lattices.

Such symmetry groups consist of translations by vectors of the form

$\mathbf{R} = n_1 \mathbf{a}_1 + n_2 \mathbf{a}_2 + n_3 \mathbf{a}_3,$

where n₁, n₂, and n₃ are integers and a₁, a₂, and a₃ are three non-coplanar vectors, called primitive vectors.

These lattices are classified by space group of the translation lattice itself; there are 14 Bravais lattices in three dimensions; each can apply in one lattice system only. They represent the maximum symmetry a structure with the translational symmetry concerned can have.

All crystalline materials must, by definition fit in one of these arrangements (not including quasicrystals).

For convenience a Bravais lattice is depicted by a unit cell which is a factor 1, 2, 3 or 4 larger than the primitive cell. Depending on the symmetry of a crystal or other pattern, the fundamental domain is again smaller, up to a factor 48.

The Bravais lattices were studied by Moritz Ludwig Frankenheim (1801-1869), in 1842, who found that there were 15 Bravais lattices. This was corrected to 14 by A. Bravais in 1848.

See also

• Crystal cluster
• Crystal structure
• List of the 230 crystallographic 3D space groups

References

• Hahn, Theo, ed. (2002), International Tables for Crystallography, Volume A: Space Group Symmetry, A (5th ed.), Berlin, New York: Springer-Verlag, doi:10.1107/97809553602060000100, ISBN 978-0-7923-6590-7, http://it.iucr.org/A/ 

External links

• Overview of the 32 groups
• Mineral galleries - Symmetry
• all cubic crystal classes, forms and stereographic projections (interactive java applet)
• Crystal system at the Online Dictionary of Crystallography
• Crystal family at the Online Dictionary of Crystallography
• Lattice system at the Online Dictionary of Crystallography
• Conversion Primitive to Standard Conventional for VASP input files
• Learning Crystallography