Passive differentiator circuit

Figure 1: Capacitive Differentiator

Figure 2: Inductive Differentiator

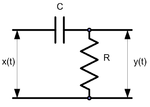
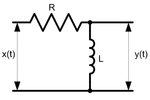
A passive differentiator circuit is a simple four-terminal network consisting of two passive elements as shown in Figures 1 and 2. It is a simple first-order high-pass filter.

Transfer function

The analysis here is for the capacitive circuit in Figure 1. The inductive case in Figure 2 can be handled in a similar way.

The transfer function shows the dependence of the network gain on the signal frequency for sinusoidal signals.

According to Ohm's law,

$Y=X\frac{Z_R}{Z_R+Z_C}=X\frac{R}{R+\frac{1}{j \omega C}}=X\frac{1}{1+\frac{1}{j \omega RC}},$

where X and Y are input and output signals' amplitudes respectively, and Z_R and Z_C are the resistor's and capacitor's impedances. Therefore, the complex transfer function is

$K(j \omega)=\frac{1}{1+\frac{1}{j \omega RC}}=\frac{1}{1+\frac{\omega_0}{j \omega}},$

where

$\omega_0=\frac{1}{RC}.$

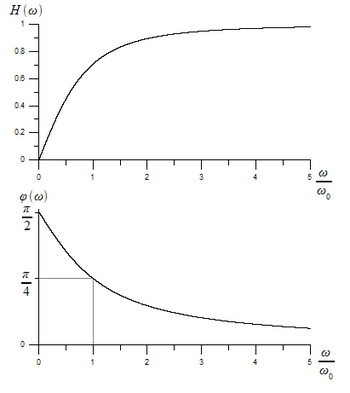
The amplitude transfer function

$H(\omega)\triangleq|K(j \omega)|=\frac{1}{\sqrt{1+\left(\frac{\omega_0}{\omega}\right)^2}},$

and the phase transfer function

$\phi (\omega)\triangleq\arg K(j \omega)=\arctan \frac{\omega_0}{\omega},$

which are both shown in Figure 3.

Figure 3: Amplitude and phase transfer functions for a passive differentiator circuit

Transfer functions for the second circuit are the same (with $\omega_0=\frac{R}{L}$).

Impulse response

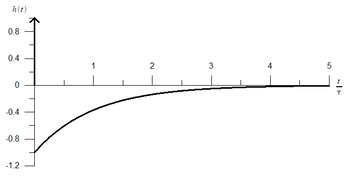
The circuit's impulse response, which is shown in Figure 4, can be derived as an inverse Laplace transform of the complex transfer function:

$h(t)=\mathcal{L}^{-1} \left \{K(p) \right \}=\delta (t)-\omega_0 e^{-\omega_0 t}=\delta (t)-\frac{1}{\tau} e^{-\frac{t}{\tau}}$

where $\tau=\frac{1}{\omega_0}$ is a time constant, and δ(t) is a Dirac delta function.

Figure 4: An impulse response of a passive differentiator circuit

Applications

A passive differentiator circuit is one of the basic electronic circuits, being widely used in circuit analysis based on the equivalent circuit method.

See also

• Passive integrator circuit
• RC circuit
• Electronic filter