- Process capability index
-
In process improvement efforts, the process capability index or process capability ratio is a statistical measure of process capability: The ability of a process to produce output within specification limits.[1] The concept of process capability only holds meaning for processes that are in a state of statistical control. Process capability indices measure how much "natural variation" a process experiences relative to its specification limits and allows different processes to be compared with respect to how well an organization controls them.
If the upper and lower specification limits of the process are USL and LSL, the target process mean is T, the estimated mean of the process is
 and the estimated variability of the process (expressed as a standard deviation) is
and the estimated variability of the process (expressed as a standard deviation) is  , then commonly-accepted process capability indices include:
, then commonly-accepted process capability indices include:Index Description 
Estimates what the process is capable of producing if the process mean were to be centered between the specification limits. Assumes process output is approximately normally distributed. 
Estimates process capability for specifications that consist of a lower limit only (for example, strength). Assumes process output is approximately normally distributed. 
Estimates process capability for specifications that consist of an upper limit only (for example, concentration). Assumes process output is approximately normally distributed. ![\hat{C}_{pk} = \min \Bigg[ {USL - \hat{\mu} \over 3 \hat{\sigma}}, { \hat{\mu} - LSL \over 3 \hat{\sigma}} \Bigg]](4/5d4e5de7cb0c59aae21a8d846f2f8555.png)
Estimates what the process is capable of producing, considering that the process mean may not be centered between the specification limits. (If the process mean is not centered,  overestimates process capability.)
overestimates process capability.)  if the process mean falls outside of the specification limits. Assumes process output is approximately normally distributed.
if the process mean falls outside of the specification limits. Assumes process output is approximately normally distributed.
Estimates process capability around a target, T.  is always greater than zero. Assumes process output is approximately normally distributed.
is always greater than zero. Assumes process output is approximately normally distributed.  is also known as the Taguchi capability index.[2]
is also known as the Taguchi capability index.[2]
Estimates process capability around a target, T, and accounts for an off-center process mean. Assumes process output is approximately normally distributed.  is estimated using the sample standard deviation.
is estimated using the sample standard deviation.Contents
Recommended values
Process capability indices are constructed to express more desirable capability with increasingly higher values. Values near or below zero indicate processes operating off target (
 far from T) or with high variation.
far from T) or with high variation.Fixing values for minimum "acceptable" process capability targets is a matter of personal opinion, and what consensus exists varies by industry, facility, and the process under consideration. For example, in the automotive industry, the AIAG sets forth guidelines in the Production Part Approval Process, 4th edition for recommended Cpk minimum values for critical-to-quality process characteristics. However, these criteria are debatable and several processes may not be evaluated for capability just because they have not properly been assessed.
Since the process capability is a function of the specification, the Process Capability Index is only as good as the specification . For instance, if the specification came from an engineering guideline without considering the function and criticality of the part, a discussion around process capability is useless, and would have more benefits if focused on what are the real risks of having a part borderline out of specification. The loss function of Taguchi better illustrates this concept.
At least one academic expert recommends[3] the following:
Situation Recommended minimum process capability for two-sided specifications Recommended minimum process capability for one-sided specification Existing process 1.33 1.25 New process 1.50 1.45 Safety or critical parameter for existing process 1.50 1.45 Safety or critical parameter for new process 1.67 1.60 Six Sigma quality process 2.00 2.00 It should be noted though that where a process produces a characteristic with a capability index greater than 2.5, the unnecessary precision may be expensive[4].
Relationship to measures of process fallout
The mapping from process capability indices, such as Cpk, to measures of process fallout is straightforward. Process fallout quantifies how many defects a process produces and is measured by DPMO or PPM. Process yield is, of course, the complement of process fallout and is approximately equal to the area under the probability density function
 if the process output is approximately normally distributed.
if the process output is approximately normally distributed.In the short term ("short sigma"), the relationships are:
Cpk Sigma level (σ) Area under the probability density function Φ(σ) Process yield Process fallout (in terms of DPMO/PPM) 0.33 1 0.6826894921 68.27% 317311 0.67 2 0.9544997361 95.45% 45500 1.00 3 0.9973002039 99.73% 2700 1.33 4 0.9999366575 99.99% 63 1.67 5 0.9999994267 99.9999% 1 2.00 6 0.9999999980 99.9999998% 0.002 In the long term, processes can shift or drift significantly (most control charts are only sensitive to changes of 1.5σ or greater in process output), so process capability indices are not applicable as they require statistical control.
Example
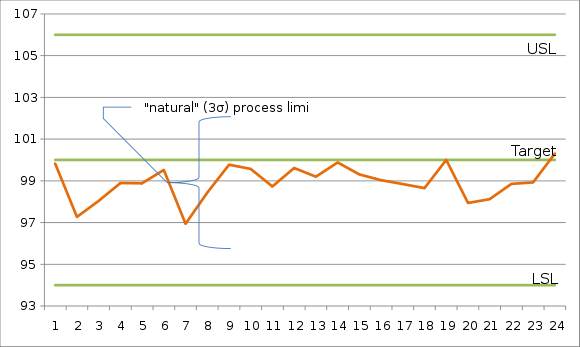
Consider a quality characteristic with target of 100.00 μm and upper and lower specification limits of 106.00 μm and 94.00 μm respectively. If, after carefully monitoring the process for a while, it appears that the process is in control and producing output predictably (as depicted in the run chart below), we can meaningfully estimate its mean and standard deviation.
If
 and
and  are estimated to be 98.94 μm and 1.03 μm, respectively, then
are estimated to be 98.94 μm and 1.03 μm, respectively, thenIndex 
![\hat{C}_{pk} = \min \Bigg[ {USL - \hat{\mu} \over 3 \hat{\sigma}}, { \hat{\mu} - LSL \over 3 \hat{\sigma}} \Bigg] = \min \Bigg[ {106.00 - 98.94 \over 3 \times 1.03}, { 98.94 - 94 \over 3 \times 1.03} \Bigg] = 1.60](8/1281127894eeb1d9c4b2686bd766c659.png)


The fact that the process is running off-center (about 1σ below its target) is reflected in the markedly different values for Cp, Cpk, Cpm, and Cpkm.
References
- ^ "What is Process Capability?". NIST/Sematech Engineering Statistics Handbook. National Institute of Standards and Technology. http://www.itl.nist.gov/div898/handbook/pmc/section1/pmc16.htm. Retrieved 2008-06-22.
- ^ Boyles, Russell (1991). "The Taguchi Capability Index". Journal of Quality Technology (Milwaukee, Wisconsin: American Society for Quality Control) 23 (1): pp. 17 – 26. ISSN 0022-4065. OCLC 1800135. http://www.asq.org/pub/jqt/
- ^ Montgomery, Douglas (2004). Introduction to Statistical Quality Control. New York, New York: John Wiley & Sons, Inc.. p. 776. ISBN 9780471656319. OCLC 56729567. http://www.eas.asu.edu/~masmlab/montgomery/.
- ^ Booker, J. M.; Raines, M.; Swift, K. G. (2001). Designing Capable and Reliable Products. Oxford: Butterworth-Heinemann. ISBN 9780750650762. OCLC 47030836.
See also
Categories:- Index numbers
- Process management
- Quality control
Wikimedia Foundation. 2010.