Mesh analysis

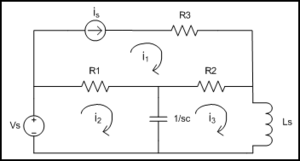
Figure 1: Essential Meshes of the planar circuit labeled 1, 2, and 3. R1, R2, R3, 1/sc, and Ls represent the impedance of the resistors, capacitor, and inductor values in the s-domain. Vs and Is are the values of the voltage source and current source respectively.

Mesh analysis (or the mesh current method) is a method that is used to solve planar circuits for the currents (and indirectly the voltages) at any place in the circuit. Planar circuits are circuits that can be drawn on a plane surface with no wires crossing each other. A more general technique, called loop analysis can be applied to any circuit, planar or not. Mesh analysis and loop analysis both make use of Kirchhoff’s voltage law to arrive at a set of equations guaranteed to be solvable if the circuit has a solution.^[1] Mesh analysis is usually easier to use when the circuit is planar, compared to loop analysis. ^[2]

Mesh currents and essential meshes

Figure 2: Circuit with Mesh Currents Labeled as i₁, i₂, and i₃. The arrows show the direction of the mesh current.

Mesh analysis works by arbitrarily assigning mesh currents in the essential meshes. An essential mesh is a loop in the circuit that does not contain any other loop. When looking at a circuit schematic, the essential meshes look like a “window pane”. Figure 1 labels the essential meshes with one, two, and three. Once the essential meshes are found, the mesh currents need to be labeled.^[3]

A mesh current is a current that loops around the essential mesh. The mesh current might not have a physical meaning but it is used to set up the mesh analysis equations.^[2] When assigning the mesh currents it is important to have all the mesh currents loop in the same direction. This will help prevent errors when writing out the equations. The convention is to have all the mesh currents looping in a clockwise direction.^[3] Figure 2 shows the same circuit shown before but with the mesh currents labeled.

The reason to use mesh currents instead of just using KCL and KVL to solve a problem is that the mesh currents can account for any unnecessary currents that may be drawn in when using KCL and KVL. Mesh analysis ensures that the least possible number of equations regarding currents is used, greatly simplifying the problem.

Setting up the equations

Figure 3: Simple Circuit using Mesh Analysis

After labeling the mesh currents, one only needs to write one equation per mesh in order to solve for all the currents in the circuit. These equations are the sum of the voltage drops in a complete loop of the mesh current.^[3] For other than current and voltage sources, the voltage drops will be the impedance of the electronic component multiplied by the mesh current in that loop. It is important to note that if a component exists between two essential meshes, the component's voltage drop will be the impedance of the component times the present mesh current minus the neighboring mesh current (computing the subtraction first).^[4]

If a voltage source is present within the mesh loop, the voltage at the source is either added or subtracted depending on if it is a voltage drop or a voltage rise in the direction of the mesh current. For a current source that is not contained between two meshes, the mesh current will take the positive or negative value of the current source depending on if the mesh current is in the same or opposite direction of the current source.^[3] The following is the same circuit from above with the equations needed to solve for all the currents in the circuit.

$\begin{cases} \text{Mesh 1: } i_1 = i_s\\ \text{Mesh 2: } -V_s + R_1(i_2-i_1) + \frac{1}{sc}(i_2-i_3)=0\\ \text{Mesh 3: } \frac{1}{sc}(i_3-i_2) + R_2(i_3-i_1) + Lsi_3=0\\ \end{cases} \,$

Once the equations are found, the system of linear equations can be solved by using any technique to solve linear equations.

Special cases

There are two special cases in mesh current: supermesh and dependent sources.

Supermesh

Figure 4: Circuit with a supermesh. Supermesh occurs because the current source is in between the essential meshes.

A supermesh occurs when a current source is contained between two essential meshes. To handle the supermesh, first treat the circuit as if the current source is not there. This leads to one equation that incorporates two mesh currents. Once this equation is formed, an equation is needed that relates the two mesh currents with the current source. This will be an equation where the current source is equal to one of the mesh currents minus the other. The following is a simple example of dealing with a supermesh.^[2]

$\begin{cases} \text{Mesh 1, 2: } -V_s + R_1i_1 + R_2i_2 = 0\\ \text{Current source: } i_s = i_2 - i_1 \end{cases} \,$

Dependent sources

Figure 5: Circuit with dependent source. i_x is the current that the dependent voltage source depends on.

A dependent source is a current source or voltage source that depends on the voltage or current on another element in the circuit. When a dependent source is contained within an essential mesh, the dependent source should be treated like a normal source. After the mesh equation is formed, a dependent source equation is needed. This equation is generally called a constraint equation. This is an equation that relates the dependent source’s variable to the voltage or current that the source depends on in the circuit. The following is a simple example of a dependent source.^[2]

$\begin{cases} \text{Mesh 1: } -V_s + R_1i_1 + R_3(i_1 - i_2) = 0\\ \text{Mesh 2: } R_2i_2 + 3i_x + R_3(i_2 - i_1) = 0\\ \text{Dependent variable: } i_x = i_1 - i_2 \end{cases} \,$

See also

• Ohm's law
• Analysis of resistive circuits
• Nodal analysis
• Kirchhoff's circuit laws
• Source transformation

External links

• Mesh current method
• Online three-mesh problem solver

References

1. ^ Hayt, William H., & Kemmerly, Jack E. (1993). Engineering Circuit Analysis (5th ed.), New York: McGraw Hill.
2. ^ ^{a b c d} Nilsson, James W., & Riedel, Susan A. (2002). Introductory Circuits for Electrical and Computer Engineering. New Jersey: Prentice Hall.
3. ^ ^{a b c d} Lueg, Russell E., & Reinhard, Erwin A. (1972). Basic Electronics for Engineers and Scientists (2nd ed.). New York: International Textbook Company.
4. ^ Puckett, Russell E., & Romanowitz, Harry A. (1976). Introduction to Electronics (2nd ed.). San Francisco: John Wiley and Sons, Inc.