Oriented matroid

Oriented-matroid theory allows a combinatorial approach to the max-flow min-cut theorem. A network with the value of flow equal to the capacity of an s-t cut

An oriented matroid is a mathematical structure that abstracts the properties of directed graphs and of arrangements of vectors in a vector space over an ordered field (particularly for partially ordered vector spaces).^[1] In comparison, an ordinary (i.e., non-oriented) matroid abstracts the dependence properties that are common both to graphs, which are not necessarily directed, and to arrangements of vectors over fields, which are not necessarily ordered.^[2] ^[3]

All oriented matroids have an underlying matroid. Thus, results on ordinary matroids can be applied to oriented matroids. However, the converse is false; some matroids cannot become an oriented matroid by orienting an underlying structure (e.g., circuits or independent sets).^[4] The distinction between matroids and oriented matroids is discussed further below.

Matroids are often useful in areas such as dimension theory and algorithms. Because of an oriented matroid's inclusion of additional details about the oriented nature of a structure, its usefulness extends further into several areas including geometry and optimization.

1 Axiomatizations
- 1.1 Circuit axioms
  - 1.1.1 Signed sets
  - 1.1.2 Axioms
2 Examples
3 Results
4 References
5 Further reading
6 External links

Axiomatizations

Like ordinary matroids, several equivalent systems of axioms exist. (Such structures that possess multiple equivalent axiomatizations are called cryptomorphic.)

Circuit axioms

Signed sets

Before we list the circuit axioms a few terms must be defined.

A signed set, $X$ , combines a set of objects $\underline{X}$ with a partition of that set into two subsets: $X +$ and $X -$ .

The members of

X +

are called the positive elements; members of

X -

are the negative elements.

The set $\underline{X} = X^+ \cup X^-$ is called the support of $X$ .

The empty signed set, $\empty$ is defined in the obvious way.

The signed set $Y$ is the opposite of $X$ , i.e., $Y = - X$ , if and only if $Y + = X -$ and $Y - = X +$

The concept of signed sets is key to distinguishing oriented from ordinary matroids.

Axioms

Let $E$ be any set. We refer to $E$ as the ground set. Let $\mathcal{C}$ be a collection of signed sets, each of which is supported by a subset of $E$ . If the following axioms hold for $\mathcal{C}$ , then equivalently $\mathcal{C}$ is the set of signed circuits for an oriented matroid on $E$ .

(C0) $\empty \notin \mathcal{C}$

(C1) (symmetric) $\mathcal{C} = -\mathcal{C}$

(C2) (incomparable) $\mbox{ for all } X,Y \in \mathcal{C} \mbox{ if } \underline{X} \subseteq \underline{Y}, \mbox{ then } X=Y \mbox{ or } X = -Y$

(C3) (weak elimination)
- $Z^+ \subseteq (X^+ \cup Y^+)\setminus\{e\} \mbox{ and }$
- $Z^- \subseteq (X^- \cup Y^-)\setminus\{e\}.$

Examples

A simple directed acyclic graph

Oriented matroids are often introduced (e.g., Bachem and Kern) as an abstraction for directed graphs or systems of linear inequalities. Thus, it may be helpful to first be knowledgeable of the structures for which oriented matroids are an abstraction. Several of these topics are listed below.

Directed graphs

Main article: Directed graph

Linear optimization

A 3-dimensional convex polytope

Main articles: Linear programming and Criss-cross algorithm

See also: Simplex algorithm and Bland's rule

The theory of oriented matroids was initiated by R. Tyrrell Rockafellar to describe the sign patterns of the matrices arising through the pivoting operations of Dantzig's simplex algorithm; Rockafellar was inspired by Albert W. Tucker studies of such sign patterns in "Tucker tableaux".^[5] Much of the theory of oriented matroids (OMs) was developed to study the combinatorial invariants of linear-optimization, particularly those visible in the basis-exchange pivoting of the simplex algorithm.^[6]

Convex polytope

Main article: Convex polytope

For example, Ziegler introduces oriented matroids via convex polytopes.

Results

Algebra: duality and polarity

Oriented matroids have a satisfying theory of duality.^[7]

Geometry

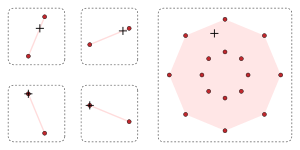Minkowski addition of four line-segments. The left-hand pane displays four sets, which are displayed in a two-by-two array. Each of the sets contains exactly two points, which are displayed in red. In each set, the two points are joined by a pink line-segment, which is the convex hull of the original set. Each set has exactly one point that is indicated with a plus-symbol. In the top row of the two-by-two array, the plus-symbol lies in the interior of the line segment; in the bottom row, the plus-symbol coincides with one of the red-points. This completes the description of the left-hand pane of the diagram. The right-hand pane displays the Minkowski sum of the sets, which is the union of the sums having exactly one point from each summand-set; for the displayed sets, the sixteen sums are distinct points, which are displayed in red: The right-hand red sum-points are the sums of the left-hand red summand-points. The convex hull of the sixteen red-points is shaded in pink. In the pink interior of the right-hand sumset lies exactly one plus-symbol, which is the (unique) sum of the plus-symbols from the right-hand side. The right-hand plus-symbol is indeed the sum of the four plus-symbols from the left-hand sets, precisely two points from the original non-convex summand-sets and two points from the convex hulls of the remaining summand-sets.

A zonotope, which is a Minkowski sum of line segments, is a fundamental model for oriented matroids. The sixteen dark-red points (on the right) form the Minkowski sum of the four non-convex sets (on the left), each of which consists of a pair of red points. Their convex hulls (shaded pink) contain plus-signs (+): The right plus-sign is the sum of the left plus-signs.

Main article: Combinatorial geometry

See also: Convex polytope and Antimatroid

The theory of oriented matroids has influenced the development of combinatorial geometry, especially the theory of convex polytopes, zonotopes, and of configurations of vectors (arrangements of hyperplanes).^[8] Many results—Carathéodory's theorem, Helly's theorem, Radon's theorem, the Hahn–Banach theorem, the Krein–Milman theorem, the lemma of Farkas—can be formulated using appropriate oriented matroids.^[9]

Rank 3 oriented matroids are equivalent to arrangements of pseudolines.^[10]

Similarly, matroid theory is useful for developing combinatorial notions of dimension, rank, etc.

In combinatorial convexity, the notion of an antimatroid is also useful.

Optimization

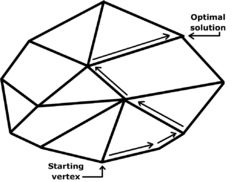In convex geometry, the simplex algorithm for linear programming is interpreted as tracing a path along the vertices of a convex polyhedron. Oriented matroid theory studies the combinatorial invariants that are revealed in the sign-patterns of the matrices that appear as pivoting algorithms exchange bases.

The theory of oriented matroids (OM) has led to break-throughs in combinatorial optimization. In linear programming, OM theory was the language in which Bland formulated his pivoting rule by which the simplex algorithm avoids cycles; similarly, OM theory was used by Terlakey and Zhang to prove that their criss-cross algorithms have finite termination for linear programming problems. Similar results were made in convex quadratic programming by Todd and Terlaky.^[11] The criss-cross algorithm is often studied using the theory of oriented matroids (OMs), which is a combinatorial abstraction of linear-optimization theory.^[6]^[12]

Historically, an OM algorithm for quadratic-programming problems and linear-complementarity problems was published by Michael J. Todd, before Terlaky and Wang published their criss-cross algorithms.^[6]^[13] However, Todd's pivoting-rule cycles on nonrealizable oriented matroids (and only on nonrealizable oriented matroids). Such cycling does not stump the OM criss-cross algorithms of Terlaky and Wang, however.^[6] There are oriented-matroid variants of the criss-cross algorithm for linear programming, for quadratic programming, and for the linear-complementarity problem.^[6]^[6]^[14]^[14] Oriented matroid theory is used in many areas of optimization, besides linear programming. OM theory has been applied to linear-fractional programming^[15] quadratic-programming problems, and linear complementarity problems.^[14]^[16]^[17]

Outside of combinatorial optimization, OM theory also appears in convex minimization in Rockafellar's theory of "monotropic programming" and related notions of "fortified descent".^[18]

Similarly, matroid theory has influenced the development of combinatorial algorithms, particularly the greedy algorithm.^[19] More generally, a greedoid is useful for studying the finite termination of algorithms.

References

^ Rockafellar 1969. Björner et alia, Chapters 1-3. Bokowski, Chapter 1. Ziegler, Chapter 7.
^ Björner et alia, Chapters 1-3. Bokowski, Chapters 1-4.
^ Because matroids and oriented matroids are abstractions of other mathematical abstractions, nearly all the relevant books are written for mathematical scientists rather than for the general public. For learning about oriented matroids, a good preparation is to study the textbook on linear optimization by Nering and Tucker, which is infused with oriented-matroid ideas, and then to proceed to Ziegler's lectures on polytopes.
^ Björner et alia, Chapter 7.9.
^ (Rockafellar 1969):
Rockafellar, R. T. (1969). "The elementary vectors of a subspace of $R N$ (1967)". In R. C. Bose and T. A. Dowling. Combinatorial Mathematics and its Applications. The University of North Carolina Monograph Series in Probability and Statistics. Chapel Hill, North Carolina: University of North Carolina Press.. pp. 104–127. MR 278972. PDF reprint. http://www.math.washington.edu/~rtr/papers/rtr-ElemVectors.pdf.
^ ^a ^b ^c ^d ^e ^f Björner, Anders; Las Vergnas, Michel; Sturmfels, Bernd; White, Neil; Ziegler, Günter (1999). "10 Linear programming". Oriented Matroids. Cambridge University Press. pp. 417–479. doi:10.1017/CBO9780511586507. ISBN 9780521777506. MR 1744046. http://ebooks.cambridge.org/ebook.jsf?bid=CBO9780511586507.
^ In oriented-matroid theory, duality differs from polarity; see Bachem and Kern, Chapters 5.11, 6, 7.2.
^ Bachem and Kern, Chapters 1–2 and 4–9. Björner et alia, Chapters 1–8. Ziegler, Chapter 7–8. Bokowski, Chapters 7–10.
^ Bachem and Wanka, Chapters 1–2, 5, 7–9. Björner et alia, Chapter 8.
^ Björner et alia, Chapter 6.
^ Björner et alia, Chapters 8-9. Fukuda and Terlaky. Compare Ziegler.
^ The theory of oriented matroids was initiated by R. Tyrrell Rockafellar to describe the sign patterns of the matrices arising through the pivoting operations of Dantzig's simplex algorithm; Rockafellar was inspired by Albert W. Tucker studies of such sign patterns in "Tucker tableaux". (Rockafellar 1969):
Rockafellar, R. T. (1969). "The elementary vectors of a subspace of $R N$ (1967)". In R. C. Bose and T. A. Dowling. Combinatorial Mathematics and its Applications. The University of North Carolina Monograph Series in Probability and Statistics. Chapel Hill, North Carolina: University of North Carolina Press.. pp. 104–127. MR 278972. PDF reprint. http://www.math.washington.edu/~rtr/papers/rtr-ElemVectors.pdf.
^ Todd, Michael J. (1985). "Linear and quadratic programming in oriented matroids". Journal of Combinatorial Theory. Series B 39 (2): 105–133. doi:10.1016/0095-8956(85)90042-5. MR 811116.
^ ^a ^b ^c Fukuda & Terlaky (1997)
^ Illés, Szirmai & Terlaky (1999)
^ Fukuda & Terlaky (1997, p. 385)
^ Fukuda & Namiki (1994, p. 367)
^ Rockafellar 1984 and 1998.
^ Lawler. Rockafellar 1984 and 1998.

External links

Categories:

Matroid theory
Convex geometry
Combinatorics
Discrete geometry
Dimension
Duality theories
Oriented matroids

Wikimedia Foundation. 2010.

Игры ⚽ Поможем написать курсовую

Look at other dictionaries:

Matroid — In combinatorics, a branch of mathematics, a matroid ( /ˈmeɪ … Wikipedia
Mnev's universality theorem — In algebraic geometry, Mnev s universality theorem is a result which can be used to represent algebraic (or semi algebraic) varieties as realizations of oriented matroids, a notion of combinatorics. Contents 1 Oriented matroids 2 Stable… … Wikipedia
Criss-cross algorithm — This article is about an algorithm for mathematical optimization. For the naming of chemicals, see crisscross method. The criss cross algorithm visits all 8 corners of the Klee–Minty cube in the worst case. It visits 3 additional… … Wikipedia
Separoid — In mathematics, a separoid is a relation defined in pairs of disjoint sets which is stable as an ideal in the canonical order induced by the contention. Many mathematical objects which appear to be quite different, find a common generalisation in … Wikipedia
Shannon switching game — The Shannon switching game is an abstract strategy game for two players, invented by the father of information theory , Claude Shannon, and (at least in its common rectangular grid form) independently invented by David Gale; it has also been… … Wikipedia
Linear programming — (LP, or linear optimization) is a mathematical method for determining a way to achieve the best outcome (such as maximum profit or lowest cost) in a given mathematical model for some list of requirements represented as linear relationships.… … Wikipedia
Flow network — In graph theory, a flow network is a directed graph where each edge has a capacity and each edge receives a flow. The amount of flow on an edge cannot exceed the capacity of the edge. Often in Operations Research, a directed graph is called a… … Wikipedia
Convex polytope — A 3 dimensional convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n dimensional space Rn.[1] Some authors use the terms convex polytope and convex… … Wikipedia
Signed graph — In the area of graph theory in mathematics, a signed graph is a graph in which each edge has a positive or negative sign.Formally, a signed graph Sigma; is a pair ( G , sigma;) that consists of a graph G = ( V , E ) and a sign mapping or… … Wikipedia
Pseudoforest — A 1 forest (a maximal pseudoforest), formed by three 1 trees In graph theory, a pseudoforest is an undirected graph[1] in which every connected component has at most one cycle. That is, it is a system of vertices and edges connecting pairs of ve … Wikipedia

Academic Dictionaries and Encyclopedias

Oriented matroid

Contents