- Max-flow min-cut theorem
-
In optimization theory, the max-flow min-cut theorem states that in a flow network, the maximum amount of flow passing from the source to the sink is equal to the minimum capacity which when removed in a specific way from the network causes the situation that no flow can pass from the source to the sink.
The max-flow min-cut theorem is a special case of the duality theorem and can be used to derive Menger's theorem and the König-Egerváry Theorem.
Contents
Definition
Let N = (V,E) be a network (directed graph) with s and t being the source and the sink of N respectively.
- The capacity of an edge is a mapping c: E→R+, denoted by cuv or c(u,v). It represents the maximum amount of flow that can pass through an edge.
- A flow is a mapping f: E→R+, denoted by fuv or f(u,v), subject to the following two constraints:
 for each
for each  (capacity constraint)
(capacity constraint) for each
for each  (conservation of flows).
(conservation of flows).
- The value of flow is defined by
 , where s is the source of N. It represents the amount of flow passing from the source to the sink.
, where s is the source of N. It represents the amount of flow passing from the source to the sink.
The maximum flow problem is to maximize | f |, that is, to route as much flow as possible from s to t.
- An s-t cut C = (S,T) is a partition of V such that s∈S and t∈T. The cut-set of C is the set {(u,v)∈E | u∈S, v∈T}. Note that if the edges in the cut-set of C are removed, | f | = 0.
- The capacity of an s-t cut is defined by
 .
.
The minimum cut problem is to minimize c(S,T), that is, to determine S and T such that the capacity of the S-T cut is minimal.
Statement
The max-flow min-cut theorem states
- The maximum value of an s-t flow is equal to the minimum capacity of an s-t cut.
Linear program formulation
The max-flow problem and min-cut problem can be formulated as two primal-dual linear programs.
Max-flow (Primal)
Min-cut (Dual)
maximize

minimize

subject to

subject to

The equality in the max-flow min-cut theorem follows from the strong duality theorem, which states that if the primal program has an optimal solution, x*, then the dual program also has an optimal solution, y*, such that the optimal values formed by the two solutions are equal.
Example
The figure on the right is a network having a value of flow of 7. The vertex in white and the vertices in grey form the subsets S and T of an s-t cut, whose cut-set contains the dashed edges. Since the capacity of the s-t cut is 7, which is equal to the value of flow, the max-flow min-cut theorem tells us that the value of flow and the capacity of the s-t cut are both optimal in this network.
Application
Generalized max-flow min-cut theorem
In addition to edge capacity, consider there is capacity at each vertex, that is, a mapping c: V→R+, denoted by c(v), such that the flow f has to satisfy not only the capacity constraint and the conservation of flows, but also the vertex capacity constraint
 for each
for each 
In other words, the amount of flow passing through a vertex cannot exceed its capacity. Define an s-t cut to be the set of vertices and edges such that for any path from s to t, the path contains a member of the cut. In this case, the capacity of the cut is the sum the capacity of each edge and vertex in it.
In this new definition, the generalized max-flow min-cut theorem states that the maximum value of an s-t flow is equal to the minimum capacity of an s-t cut in the new sense.
Menger's theorem
See also: Menger's TheoremIn the undirected edge-disjoint paths problem, we are given an undirected graph G = (V, E) and two vertices s and t, and we have to find the maximum number of edge-disjoint s-t paths in G.
The Menger's theorem states that the maximum number of edge-disjoint s-t paths in an undirected graph is equal to the minimum number of edges in an s-t cut-set.
Project selection problem
See also: Maximum flow problemIn the project selection problem, there are n projects and m equipments. Each project pi yields revenue r(pi) and each equipment qj costs c(qj) to purchase. Each project requires a number of equipments and each equipment can be shared by several projects. The problem is to determine which projects and equipments should be selected and purchased respectively, so that the profit is maximized.
Let P be the set of projects not selected and Q be the set of equipments purchased, then the problem can be formulated as,
Since r(pi) and c(qj) are positive, this maximization problem can be formulated as a minimization problem instead, that is,
The above minimization problem can then be formulated as a minimum-cut problem by constructing a network, where the source is connected to the projects with capacity r(pi), and the sink is connected by the equipments with capacity c(qj). An edge (pi, qj) with infinite capacity is added if project pi requires equipment qj. The s-t cut-set represents the projects and equipments in P and Q respectively. By the max-flow min-cut theorem, one can solve the problem as a maximum flow problem.
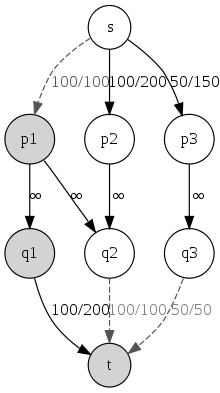
The figure on the right gives a network formulation of the following project selection problem:
Project r(pi)
Equipment c(qj)
1 100 200 Project 1 requires equipments 1 and 2.
2 200 100 Project 2 requires equipment 2.
3 150 50 Project 3 requires equipment 3.
The minimum capacity of a s-t cut is 250 and the sum of the revenue of each project is 450; therefore the maximum profit g is 450 − 250 = 200, by selecting projects p2 and p3.
History
The max-flow min-cut theorem was proved by P. Elias, A. Feinstein, and C.E. Shannon in 1956, and independently also by L.R. Ford, Jr. and D.R. Fulkerson in the same year.
See also
- Linear programming
- Maximum flow
- Minimum cut
- Flow network
- Edmonds-Karp algorithm
References
- Eugene Lawler (2001). "4.5. Combinatorial Implications of Max-Flow Min-Cut Theorem, 4.6. Linear Programming Interpretation of Max-Flow Min-Cut Theorem". Combinatorial Optimization: Networks and Matroids. Dover. pp. 117–120. ISBN 0486414531.
- Christos H. Papadimitriou, Kenneth Steiglitz (1998). "6.1 The Max-Flow, Min-Cut Theorem". Combinatorial Optimization: Algorithms and Complexity. Dover. pp. 120–128. ISBN 0486402584.
- Vijay V. Vazirani (2004). "12. Introduction to LP-Duality". Approximation Algorithms. Springer. pp. 93–100. ISBN 3540653678.
Categories:- Combinatorial optimization
- Theorems in discrete mathematics
Wikimedia Foundation. 2010.