Ant colony optimization algorithms

Ant behavior was the inspiration for the metaheuristic optimization technique.

In computer science and operations research, the ant colony optimization algorithm (ACO) is a probabilistic technique for solving computational problems which can be reduced to finding good paths through graphs.

This algorithm is a member of ant colony algorithms family, in swarm intelligence methods, and it constitutes some metaheuristic optimizations. Initially proposed by Marco Dorigo in 1992 in his PhD thesis,^[1][2] the first algorithm was aiming to search for an optimal path in a graph, based on the behavior of ants seeking a path between their colony and a source of food. The original idea has since diversified to solve a wider class of numerical problems, and as a result, several problems have emerged, drawing on various aspects of the behavior of ants.

Overview

Summary

In the natural world, ants (initially) wander randomly, and upon finding food return to their colony while laying down pheromone trails. If other ants find such a path, they are likely not to keep travelling at random, but to instead follow the trail, returning and reinforcing it if they eventually find food (see Ant communication).

Over time, however, the pheromone trail starts to evaporate, thus reducing its attractive strength. The more time it takes for an ant to travel down the path and back again, the more time the pheromones have to evaporate. A short path, by comparison, gets marched over more frequently, and thus the pheromone density becomes higher on shorter paths than longer ones. Pheromone evaporation also has the advantage of avoiding the convergence to a locally optimal solution. If there were no evaporation at all, the paths chosen by the first ants would tend to be excessively attractive to the following ones. In that case, the exploration of the solution space would be constrained.

Thus, when one ant finds a good (i.e., short) path from the colony to a food source, other ants are more likely to follow that path, and positive feedback eventually leads all the ants following a single path. The idea of the ant colony algorithm is to mimic this behavior with "simulated ants" walking around the graph representing the problem to solve.

Detailed

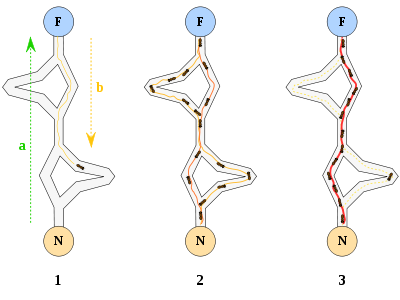
The original idea comes from observing the exploitation of food resources among ants, in which ants’ individually limited cognitive abilities have collectively been able to find the shortest path between a food source and the nest.

1. The first ant finds the food source (F), via any way (a), then returns to the nest (N), leaving behind a trail pheromone (b)
2. Ants indiscriminately follow four possible ways, but the strengthening of the runway makes it more attractive as the shortest route.
3. Ants take the shortest route, long portions of other ways lose their trail pheromones.

In a series of experiments on a colony of ants with a choice between two unequal length paths leading to a source of food, biologists have observed that ants tended to use the shortest route. ^{[3] [4]} A model explaining this behaviour is as follows:

1. An ant (called "blitz") runs more or less at random around the colony;
2. If it discovers a food source, it returns more or less directly to the nest, leaving in its path a trail of pheromone;
3. These pheromones are attractive, nearby ants will be inclined to follow, more or less directly, the track;
4. Returning to the colony, these ants will strengthen the route;
5. If there are two routes to reach the same food source then, in a given amount of time, the shorter one will be traveled by more ants than the long route;
6. The short route will be increasingly enhanced, and therefore become more attractive;
7. The long route will eventually disappear because pheromones are volatile;
8. Eventually, all the ants have determined and therefore "chosen" the shortest route.

Ants use the environment as a medium of communication. They exchange information indirectly by depositing pheromones, all detailing the status of their "work". The information exchanged has a local scope, only an ant located where the pheromones were left has a notion of them. This system is called "Stigmergy" and occurs in many social animal societies (it has been studied in the case of the construction of pillars in the nests of termites). The mechanism to solve a problem too complex to be addressed by single ants is a good example of a self-organized system. This system is based on positive feedback (the deposit of pheromone attracts other ants that will strengthen it themselves) and negative (dissipation of the route by evaporation prevents the system from thrashing). Theoretically, if the quantity of pheromone remained the same over time on all edges, no route would be chosen. However, because of feedback, a slight variation on an edge will be amplified and thus allow the choice of an edge. The algorithm will move from an unstable state in which no edge is stronger than another, to a stable state where the route is composed of the strongest edges.

The basic philosophy of the algorithm involves the movement of a colony of ants through the different states of the problem influenced by two local decision policies, viz., trails and attractiveness. Thereby, each such ant incrementally constructs a solution to the problem. When an ant completes a solution, or during the construction phase, the ant evaluates the solution and modifies the trail value on the components used in its solution. This pheromone information will direct the search of the future ants. Furthermore, the algorithm also includes two more mechanisms, viz., trail evaporation and daemon actions. Trail evaporation reduces all trail values over time thereby avoiding any possibilities of getting stuck in local optima. The daemon actions are used to bias the search process from a non-local perspective.

Common extensions

Here are some of most popular variations of ACO Algorithms

Elitist ant system

The global best solution deposits pheromone on every iteration along with all the other ants.

Max-Min ant system (MMAS)

Added Maximum and Minimum pheromone amounts [τ_max,τ_min] Only global best or iteration best tour deposited pheromone. All edges are initialized to τ_max and reinitialized to τ_max when nearing stagnation. ^[5]

Ant Colony System

It has been presented above.^[6]

Rank-based ant system (ASrank)

All solutions are ranked according to their length. The amount of pheromone deposited is then weighted for each solution, such that solutions with shorter paths deposit more pheromone than the solutions with longer paths.

Continuous orthogonal ant colony (COAC)

The pheromone deposit mechanism of COAC is to enable ants to search for solutions collaboratively and effectively. By using an orthogonal design method, ants in the feasible domain can explore their chosen regions rapidly and efficiently, with enhanced global search capability and accuracy.

The orthogonal design method and the adaptive radius adjustment method can also be extended to other optimization algorithms for delivering wider advantages in solving practical problems.^[7]

Convergence

For some versions of the algorithm, it is possible to prove that it is convergent (i.e. it is able to find the global optimum in a finite time). The first evidence of a convergence ant colony algorithm was made in 2000, the graph-based ant system algorithm, and then algorithms for ACS and MMAS. Like most metaheuristics, it is very difficult to estimate the theoretical speed of convergence. In 2004, Zlochin and his colleagues^[8] showed that COA-type algorithms could be assimilated methods of stochastic gradient descent, on the cross-entropy and estimation of distribution algorithm. They proposed these metaheuristics as a "research-based model".

Example pseudo-code and formulae

  procedure ACO_MetaHeuristic
    while(not_termination)
       generateSolutions()
       daemonActions()
       pheromoneUpdate()
    end while
  end procedure

Edge selection

An ant is a simple computational agent in the ant colony optimization algorithm. It iteratively constructs a solution for the problem at hand. The intermediate solutions are referred to as solution states. At each iteration of the algorithm, each ant moves from a state x to state y, corresponding to a more complete intermediate solution. Thus, each ant k computes a set A_k(x) of feasible expansions to its current state in each iteration, and moves to one of these in probability. For ant k, the probability $p_{xy}^k$ of moving from state x to state y depends on the combination of two values, viz., the attractiveness η_xy of the move, as computed by some heuristic indicating the a priori desirability of that move and the trail level τ_xy of the move, indicating how proficient it has been in the past to make that particular move.

The trail level represents a posteriori indication of the desirability of that move. Trails are updated usually when all ants have completed their solution, increasing or decreasing the level of trails corresponding to moves that were part of "good" or "bad" solutions, respectively.

In general, the kth ant moves from state x to state y with probability

$p_{xy}^k = \frac { (\tau_{xy}^{\alpha}) (\eta_{xy}^{\beta}) } { \sum (\tau_{xy}^{\alpha}) (\eta_{xy}^{\beta}) }$

where

τ_xy is the amount of pheromone deposited for transition from state x to y, 0 ≤ α is a parameter to control the influence of τ_xy, η_xy is the desirability of state transition xy (a priori knowledge, typically 1 / d_xy, where d is the distance) and β ≥ 1 is a parameter to control the influence of η_xy.

Pheromone update

When all the ants have completed a solution, the trails are updated by $\tau^{k}_{xy} = (1-\rho)\tau^{k}_{xy} + \Delta \tau^{k}_{xy}$

where

$\tau^{k}_{xy}$ is the amount of pheromone deposited for a state transition xy, ρ is the pheromone evaporation coefficient and $\Delta \tau^{k}_{i,j}$ is the amount of pheromone deposited, typically given for a TSP problem (with moves corresponding to arcs of the graph) by

$\Delta \tau^{k}_{xy} = \begin{cases} Q/L_k & \mbox{if ant }k\mbox{ uses curve }xy\mbox{ in its tour} \\ 0 & \mbox{otherwise} \end{cases}$

where L_k is the cost of the kth ant's tour (typically length) and Q is a constant.

Applications

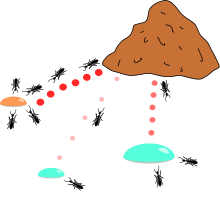Knapsack problem. The ants prefer the smaller drop of honey over the more abundant, but less nutritious, sugar.

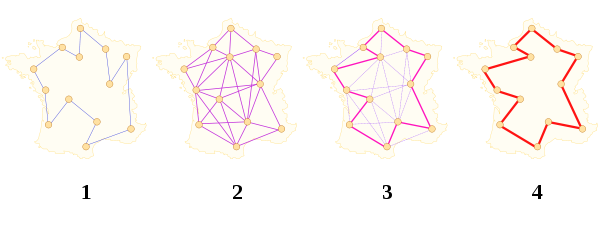
Ant colony optimization algorithms have been applied to many combinatorial optimization problems, ranging from quadratic assignment to protein folding or routing vehicles and a lot of derived methods have been adapted to dynamic problems in real variables, stochastic problems, multi-targets and parallel implementations. It has also been used to produce near-optimal solutions to the travelling salesman problem. They have an advantage over simulated annealing and genetic algorithm approaches of similar problems when the graph may change dynamically; the ant colony algorithm can be run continuously and adapt to changes in real time. This is of interest in network routing and urban transportation systems.

As a very good example, ant colony optimization algorithms have been used to produce near-optimal solutions to the travelling salesman problem. The first ACO algorithm was called the Ant system ^[9] and it was aimed to solve the travelling salesman problem, in which the goal is to find the shortest round-trip to link a series of cities. The general algorithm is relatively simple and based on a set of ants, each making one of the possible round-trips along the cities. At each stage, the ant chooses to move from one city to another according to some rules:

1. It must visit each city exactly once;
2. A distant city has less chance of being chosen (the visibility);
3. The more intense the pheromone trail laid out on an edge between two cities, the greater the probability that that edge will be chosen;
4. Having completed its journey, the ant deposits more pheromones on all edges it traversed, if the journey is short;
5. After each iteration, trails of pheromones evaporate.

Scheduling problem

• Job-shop scheduling problem (JSP)^[10]
• Open-shop scheduling problem (OSP)^[11][12]
• Permutation flow shop problem (PFSP)^[13]
• Single machine total tardiness problem (SMTTP)^[14]
• Single machine total weighted tardiness problem (SMTWTP)^[15][16][17]
• Resource-constrained project scheduling problem (RCPSP)^[18]
• Group-shop scheduling problem (GSP)^[19]
• Single-machine total tardiness problem with sequence dependent setup times (SMTTPDST)^[20]
• Multistage Flowshop Scheduling Problem (MFSP) with sequence dependent setup/changeover times^[21]

Vehicle routing problem

• Capacitated vehicle routing problem (CVRP)^[22][23][24]
• Multi-depot vehicle routing problem (MDVRP)^[25]
• Period vehicle routing problem (PVRP)^[26]
• Split delivery vehicle routing problem (SDVRP)^[27]
• Stochastic vehicle routing problem (SVRP)^[28]
• Vehicle routing problem with pick-up and delivery (VRPPD)^[29][30]
• Vehicle routing problem with time windows (VRPTW)^[31][32][33]
• Time Dependent Vehicle Routing Problem with Time Windows (TDVRPTW)^[34]

Assignment problem

• Quadratic assignment problem (QAP)^[35]
• Generalized assignment problem (GAP)^[36][37]
• Frequency assignment problem (FAP)^[38]
• Redundancy allocation problem (RAP)^[39]

Set problem

• Set covering problem(SCP)^[40][41]
• Set partition problem (SPP)^[42]
• Weight constrained graph tree partition problem (WCGTPP)^[43]
• Arc-weighted l-cardinality tree problem (AWlCTP)^[44]
• Multiple knapsack problem (MKP)^[45]
• Maximum independent set problem (MIS)^[46]

Others

• Classification^[47]
• Connection-oriented network routing^[48]
• Connectionless network routing^[49][50]
• Data mining ^{[51][47][52][53]}
• Discounted cash flows in project scheduling^[54]
• Distributed Information Retrieval^[55][56]
• Grid Workflow Scheduling Problem^[57]
• Image processing^[58][59]
• Intelligent testing system^[60]
• System identification^[61][62]
• Protein Folding^[63][64]
• Power Electronic Circuit Design^[65]

Definition difficulty

With an ACO algorithm, the shortest path in a graph, between two points A and B, is built from a combination of several paths. It is not easy to give a precise definition of what algorithm is or is not an ant colony, because the definition may vary according to the authors and uses. Broadly speaking, ant colony algorithms are regarded as populated metaheuristics with each solution represented by an ant moving in the search space. Ants mark the best solutions and take account of previous markings to optimize their search. They can be seen as probabilistic multi-agent algorithms using a probability distribution to make the transition between each iteration. In their versions for combinatorial problems, they use an iterative construction of solutions. According to some authors, the thing which distinguishes ACO algorithms from other relatives (such as algorithms to estimate the distribution or particle swarm optimization) is precisely their constructive aspect. In combinatorial problems, it is possible that the best solution eventually be found, even though no ant would prove effective. Thus, in the example of the Travelling salesman problem, it is not necessary that an ant actually travels the shortest route: the shortest route can be built from the strongest segments of the best solutions. However, this definition can be problematic in the case of problems in real variables, where no structure of 'neighbours' exists. The collective behaviour of social insects remains a source of inspiration for researchers. The wide variety of algorithms (for optimization or not) seeking self-organization in biological systems has led to the concept of "swarm intelligence", which is a very general framework in which ant colony algorithms fit.

Stigmergy algorithms

There is in practice a large number of algorithms claiming to be "ant colonies", without always sharing the general framework of optimization by canonical ant colonies (COA). In practice, the use of an exchange of information between ants via the environment (a principle called "Stigmergy") is deemed enough for an algorithm to belong to the class of ant colony algorithms. This principle has led some authors to create the term "value" to organize methods and behavior based on search of food, sorting larvae, division of labour and cooperative transportation.^[66]

Related methods

• Genetic algorithms (GA) maintain a pool of solutions rather than just one. The process of finding superior solutions mimics that of evolution, with solutions being combined or mutated to alter the pool of solutions, with solutions of inferior quality being discarded.
• Simulated annealing (SA) is a related global optimization technique which traverses the search space by generating neighboring solutions of the current solution. A superior neighbor is always accepted. An inferior neighbor is accepted probabilistically based on the difference in quality and a temperature parameter. The temperature parameter is modified as the algorithm progresses to alter the nature of the search.
• Reactive search optimization focuses on combining machine learning with optimization, by adding an internal feedback loop to self-tune the free parameters of an algorithm to the characteristics of the problem, of the instance, and of the local situation around the current solution.
• Tabu search (TS) is similar to simulated annealing in that both traverse the solution space by testing mutations of an individual solution. While simulated annealing generates only one mutated solution, tabu search generates many mutated solutions and moves to the solution with the lowest fitness of those generated. To prevent cycling and encourage greater movement through the solution space, a tabu list is maintained of partial or complete solutions. It is forbidden to move to a solution that contains elements of the tabu list, which is updated as the solution traverses the solution space.
• Artificial immune system (AIS) algorithms are modeled on vertebrate immune systems.
• Particle swarm optimization (PSO), a Swarm intelligence method
• Intelligent Water Drops (IWD), a swarm-based optimization algorithm based on natural water drops flowing in rivers
• Gravitational Search Algorithm (GSA), a Swarm intelligence method
• Ant colony clustering method (ACCM), a method that make use of clustering approach,extending the ACO.
• Stochastic diffusion search (SDS), an agent-based probabilistic global search and optimization technique best suited to problems where the objective function can be decomposed into multiple independent partial-functions

History

Chronology of COA algorithms

Chronology of Ant colony optimization algorithms.

• 1959, Pierre-Paul Grassé invented the theory of Stigmergy to explain the behavior of nest building in termites;^[67]
• 1983, Deneubourg and his colleagues studied the collective behavior of ants;^[68]
• 1988, and Moyson Manderick have an article on self-organization among ants;^[69]
• 1989, the work of Goss, Aron, Deneubourg and Pasteels on the collective behavior of Argentine ants, which will give the idea of Ant colony optimization algorithms;^[3]
• 1989, implementation of a model of behavior for food by Ebling and his colleagues;^[70]
• 1991, M. Dorigo proposed the Ant System in his doctoral thesis (which was published in 1992^[2]). A technical report extracted from the thesis and co-authored by V. Maniezzo and A. Colorni ^[71] was published five years later;^[9]
• 1996, publication of the article on Ant System;^[9]
• 1996, Hoos and Stützle invent the MAX-MIN Ant System;^[5]
• 1997, Dorigo and Gambardella publish the Ant Colony System;^[6]
• 1997, Schoonderwoerd and his colleagues developed the first application to telecommunication networks;^[72]
• 1998, Dorigo launches first conference dedicated to the ACO algorithms;^[73]
• 1998, Stützle proposes initial parallel implementations;^[74]
• 1999, Bonabeau, Dorigo and Theraulaz publish a book dealing mainly with artificial ants ^[75]
• 2000, special issue of the Future Generation Computer Systems journal on ant algorithms^[76]
• 2000, first applications to the scheduling, scheduling sequence and the satisfaction of constraints;
• 2000, Gutjahr provides the first evidence of convergence for an algorithm of ant colonies^[77]
• 2001, the first use of COA Algorithms by companies (Eurobios and AntOptima);
• 2001, IREDA and his colleagues published the first multi-objective algorithm ^[78]
• 2002, first applications in the design of schedule, Bayesian networks;
• 2002, Bianchi and her colleagues suggested the first algorithm for stochastic problem;^[79]
• 2004, Zlochin and Dorigo show that some algorithms are equivalent to the stochastic gradient descent, the cross-entropy and algorithms to estimate distribution ^[8]
• 2005, first applications to protein folding problems.

References

1. ^ A. Colorni, M. Dorigo et V. Maniezzo, Distributed Optimization by Ant Colonies, actes de la première conférence européenne sur la vie artificielle, Paris, France, Elsevier Publishing, 134-142, 1991.
2. ^ ^{a b} M. Dorigo, Optimization, Learning and Natural Algorithms, PhD thesis, Politecnico di Milano, Italie, 1992.
3. ^ ^{a b} S. Goss, S. Aron, J.-L. Deneubourg et J.-M. Pasteels, Self-organized shortcuts in the Argentine ant, Naturwissenschaften, volume 76, pages 579-581, 1989
4. ^ J.-L. Deneubourg, S. Aron, S. Goss et J.-M. Pasteels, The self-organizing exploratory pattern of the Argentine ant, Journal of Insect Behavior, volume 3, page 159, 1990
5. ^ ^{a b} T. Stützle et H.H. Hoos, MAX MIN Ant System, Future Generation Computer Systems, volume 16, pages 889-914, 2000
6. ^ ^{a b} M. Dorigo et L.M. Gambardella, Ant Colony System : A Cooperative Learning Approach to the Traveling Salesman Problem, IEEE Transactions on Evolutionary Computation, volume 1, numéro 1, pages 53-66, 1997.
7. ^ X Hu, J Zhang, and Y Li (2008). Orthogonal methods based ant colony search for solving continuous optimization problems. Journal of Computer Science and Technology, 23(1), pp.2-18.
8. ^ ^{a b} M. Zlochin, M. Birattari, N. Meuleau, et M. Dorigo, Model-based search for combinatorial optimization: A critical survey, Annals of Operations Research, vol. 131, pp. 373-395, 2004.
9. ^ ^{a b c} M. Dorigo, V. Maniezzo, et A. Colorni, Ant system: optimization by a colony of cooperating agents, IEEE Transactions on Systems, Man, and Cybernetics--Part B , volume 26, numéro 1, pages 29-41, 1996.
10. ^ D. Martens, M. De Backer, R. Haesen, J. Vanthienen, M. Snoeck, B. Baesens, Classification with Ant Colony Optimization, IEEE Transactions on Evolutionary Computation, volume 11, number 5, pages 651—665, 2007.
11. ^ B. Pfahring, "Multi-agent search for open scheduling: adapting the Ant-Q formalism," Technical report TR-96-09, 1996.
12. ^ C. Blem, "Beam-ACO, Hybridizing ant colony optimization with beam search. An application to open shop scheduling," Technical report TR/IRIDIA/2003-17, 2003.
13. ^ T. Stützle, "An ant approach to the flow shop problem," Technical report AIDA-97-07, 1997.
14. ^ A. Baucer, B. Bullnheimer, R. F. Hartl and C. Strauss, "Minimizing total tardiness on a single machine using ant colony optimization," Central European Journal for Operations Research and Economics, vol.8, no.2, pp.125-141, 2000.
15. ^ M. den Besten, "Ants for the single machine total weighted tardiness problem," Master’s thesis, University of Amsterdam, 2000.
16. ^ M, den Bseten, T. Stützle and M. Dorigo, "Ant colony optimization for the total weighted tardiness problem," Proceedings of PPSN-VI, Sixth International Conference on Parallel Problem Solving from Nature, vol. 1917 of Lecture Notes in Computer Science, pp.611-620, 2000.
17. ^ D. Merkle and M. Middendorf, "An ant algorithm with a new pheromone evaluation rule for total tardiness problems," Real World Applications of Evolutionary Computing, vol. 1803 of Lecture Notes in Computer Science, pp.287-296, 2000.
18. ^ D. Merkle, M. Middendorf and H. Schmeck, "Ant colony optimization for resource-constrained project scheduling," Proceedings of the Genetic and Evolutionary Computation Conference (GECCO 2000), pp.893-900, 2000.
19. ^ C. Blum, "ACO applied to group shop scheduling: a case study on intensification and diversification," Proceedings of ANTS 2002, vol. 2463 of Lecture Notes in Computer Science, pp.14-27, 2002.
20. ^ C. Gagné, W. L. Price and M. Gravel, "Comparing an ACO algorithm with other heuristics for the single machine scheduling problem with sequence-dependent setup times," Journal of the Operational Research Society, vol.53, pp.895-906, 2002.
21. ^ A. V. Donati, V. Darley, B. Ramachandran, "An Ant-Bidding Algorithm for Multistage Flowshop Scheduling Problem: Optimization and Phase Transitions", book chapter in Advances in Metaheuristics for Hard Optimization, Springer, ISBN 978-3-540-72959-4, pp.111-138, 2008.
22. ^ P. Toth, D. Vigo, "Models, relaxations and exact approaches for the capacitated vehicle routing problem," Discrete Applied Mathematics, vol.123, pp.487-512, 2002.
23. ^ J. M. Belenguer, and E. Benavent, "A cutting plane algorithm for capacitated arc routing problem," Computers & Operations Research, vol.30, no.5, pp.705-728, 2003.
24. ^ T. K. Ralphs, "Parallel branch and cut for capacitated vehicle routing," Parallel Computing, vol.29, pp.607-629, 2003.
25. ^ S. Salhi and M. Sari, "A multi-level composite heuristic for the multi-depot vehicle fleet mix problem," European Journal for Operations Research, vol.103, no.1, pp.95-112, 1997.
26. ^ E. Angelelli and M. G. Speranza, "The periodic vehicle routing problem with intermediate facilities," European Journal for Operations Research, vol.137, no.2, pp.233-247, 2002.
27. ^ S. C. Ho and D. Haugland, "A tabu search heuristic for the vehicle routing problem with time windows and split deliveries," Computers & Operations Research, vol.31, no.12, pp.1947-1964, 2004.
28. ^ N. Secomandi, "Comparing neuro-dynamic programming algorithms for the vehicle routing problem with stochastic demands," Computers & Operations Research, vol.27, no.11, pp.1201-1225, 2000.
29. ^ W. P. Nanry and J. W. Barnes, "Solving the pickup and delivery problem with time windows using reactive tabu search," Transportation Research Part B, vol.34, no. 2, pp.107-121, 2000.
30. ^ R. Bent and P.V. Hentenryck, "A two-stage hybrid algorithm for pickup and delivery vehicle routing problems with time windows," Computers & Operations Research, vol.33, no.4, pp.875-893, 2003.
31. ^ A. Bachem, W. Hochstattler and M. Malich, "The simulated trading heuristic for solving vehicle routing problems," Discrete Applied Mathematics, vol. 65, pp.47-72, 1996..
32. ^ [57] S. C. Hong and Y. B. Park, "A heuristic for bi-objective vehicle routing with time window constraints," International Journal of Production Economics, vol.62, no.3, pp.249-258, 1999.
33. ^ R. A. Rusell and W. C. Chiang, "Scatter search for the vehicle routing problem with time windows," European Journal for Operations Research, vol.169, no.2, pp.606-622, 2006.
34. ^ A. V. Donati, R. Montemanni, N. Casagrande, A. E. Rizzoli, L. M. Gambardella, "Time Dependent Vehicle Routing Problem with a Multi Ant Colony System", European Journal of Operational Research, vol.185, no.3, pp.1174–1191, 2008.
35. ^ T. Stützle, "MAX-MIN Ant System for the quadratic assignment problem," Technical Report AIDA-97-4, FB Informatik, TU Darmstadt, Germany, 1997.
36. ^ R. Lourenço and D. Serra "Adaptive search heuristics for the generalized assignment problem," Mathware & soft computing, vol.9, no.2-3, 2002.
37. ^ M. Yagiura, T. Ibaraki and F. Glover, "An ejection chain approach for the generalized assignment problem," INFORMS Journal on Computing, vol. 16, no. 2, pp. 133–151, 2004.
38. ^ K. I. Aardal, S. P. M.van Hoesel, A. M. C. A. Koster, C. Mannino and Antonio. Sassano, "Models and solution techniques for the frequency assignment problem," A Quarterly Journal of Operations Research, vol.1, no.4, pp.261-317, 2001.
39. ^ Y. C. Liang and A. E. Smith, "An ant colony optimization algorithm for the redundancy allocation problem (RAP)," IEEE Transactions on Reliability, vol.53, no.3, pp.417-423, 2004.
40. ^ G. Leguizamon and Z. Michalewicz, "A new version of ant system for subset problems," Proceedings of the 1999 Congress on Evolutionary Computation(CEC 99), vol.2, pp.1458-1464, 1999.
41. ^ R. Hadji, M. Rahoual, E. Talbi and V. Bachelet "Ant colonies for the set covering problem," Abstract proceedings of ANTS2000, pp.63-66, 2000.
42. ^ V Maniezzo and M Milandri, "An ant-based framework for very strongly constrained problems," Proceedings of ANTS2000, pp.222-227, 2002.
43. ^ R. Cordone and F. Maffioli,"Colored Ant System and local search to design local telecommunication networks," Applications of Evolutionary Computing: Proceedings of Evo Workshops, vol.2037, pp.60-69, 2001.
44. ^ C. Blum and M.J. Blesa, "Metaheuristics for the edge-weighted k-cardinality tree problem," Technical Report TR/IRIDIA/2003-02, IRIDIA, 2003.
45. ^ S. Fidanova, "ACO algorithm for MKP using various heuristic information", Numerical Methods and Applications, vol.2542, pp.438-444, 2003.
46. ^ G. Leguizamon, Z. Michalewicz and Martin Schutz, "An ant system for the maximum independent set problem," Proceedings of the 2001 Argentinian Congress on Computer Science, vol.2, pp.1027-1040, 2001.
47. ^ ^{a b} D. Martens, M. De Backer, R. Haesen, J. Vanthienen, M. Snoeck, B. Baesens, "Classification with Ant Colony Optimization", IEEE Transactions on Evolutionary Computation, volume 11, number 5, pages 651—665, 2007.
48. ^ G. D. Caro and M. Dorigo, "Extending AntNet for best-effort quality-of-service routing," Proceedings of the First Internation Workshop on Ant Colony Optimization (ANTS’98), 1998.
49. ^ G.D. Caro and M. Dorigo "AntNet: a mobile agents approach to adaptive routing," Proceedings of the Thirty-First Hawaii International Conference on System Science, vol.7, pp.74-83, 1998.
50. ^ G. D. Caro and M. Dorigo, "Two ant colony algorithms for best-effort routing in datagram networks," Proceedings of the Tenth IASTED International Conference on Parallel and Distributed Computing and Systems (PDCS’98), pp.541-546, 1998.
51. ^ D. Martens, B. Baesens, T. Fawcett "Editorial Survey: Swarm Intelligence for Data Mining," Machine Learning, volume 82, number 1, pp. 1-42, 2011
52. ^ R. S. Parpinelli, H. S. Lopes and A. A Freitas, "An ant colony algorithm for classification rule discovery," Data Mining: A heuristic Approach, pp.191-209, 2002.
53. ^ R. S. Parpinelli, H. S. Lopes and A. A Freitas, "Data mining with an ant colony optimization algorithm," IEEE Transaction on Evolutionary Computation, vol.6, no.4, pp.321-332, 2002.
54. ^ W. N. Chen, J. ZHANG and H. Chung, "Optimizing Discounted Cash Flows in Project Scheduling--An Ant Colony Optimization Approach", IEEE Transactions on Systems, Man, and Cybernetics--Part C: Applications and Reviews Vol.40 No.5 pp.64-77, Jan. 2010.
55. ^ D. Picard, A. Revel, M. Cord, "An Application of Swarm Intelligence to Distributed Image Retrieval", Information Sciences, 2010
56. ^ D. Picard, M. Cord, A. Revel, "Image Retrieval over Networks : Active Learning using Ant Algorithm", IEEE Transactions on Multimedia, vol. 10, no. 7, pp. 1356--1365 - nov 2008
57. ^ W. N. Chen and J. ZHANG "Ant Colony Optimization Approach to Grid Workflow Scheduling Problem with Various QoS Requirements", IEEE Transactions on Systems, Man, and Cybernetics--Part C: Applications and Reviews, Vol. 31, No. 1,pp.29-43,Jan 2009.
58. ^ S. Meshoul and M Batouche, "Ant colony system with extremal dynamics for point matching and pose estimation," Proceeding of the 16th International Conference on Pattern Recognition, vol.3, pp.823-826, 2002.
59. ^ H. Nezamabadi-pour, S. Saryazdi, and E. Rashedi, " Edge detection using ant algorithms", Soft Computing, vol. 10, no.7, pp. 623-628, 2006.
60. ^ Xiao. M.Hu, J. ZHANG, and H. Chung, "An Intelligent Testing System Embedded with an Ant Colony Optimization Based Test Composition Method", IEEE Transactions on Systems, Man, and Cybernetics--Part C: Applications and Reviews, Vol. 39, No. 6, pp. 659-669, Dec 2009.
61. ^ L. Wang and Q. D. Wu, "Linear system parameters identification based on ant system algorithm," Proceedings of the IEEE Conference on Control Applications, pp.401-406, 2001.
62. ^ K. C. Abbaspour, R. Schulin, M. T. Van Genuchten, "Estimating unsaturated soil hydraulic parameters using ant colony optimization," Advances In Water Resources, vol.24, no.8, pp.827-841, 2001.
63. ^ X. M. Hu, J. ZHANG，J. Xiao and Y. Li, "Protein Folding in Hydrophobic-Polar Lattice Model: A Flexible Ant- Colony Optimization Approach ", Protein and Peptide Letters, Volume 15, Number 5, 2008, Pp. 469-477.
64. ^ A. Shmygelska, R. A. Hernández and H. H. Hoos, "An ant colony algorithm for the 2D HP protein folding problem," Proceedings of the 3rd International Workshop on Ant Algorithms/ANTS 2002, Lecture Notes in Computer Science, vol.2463, pp.40-52, 2002.
65. ^ J. ZHANG, H. Chung, W. L. Lo, and T. Huang, "Extended Ant Colony Optimization Algorithm for Power Electronic Circuit Design", IEEE Transactions on Power Electronic. Vol.24,No.1, pp.147-162, Jan 2009.
66. ^ A. Ajith; G. Crina; R. Vitorino (éditeurs), Stigmergic Optimization, Studies in Computational Intelligence , volume 31, 299 pages, 2006. ISBN 978-3-540-34689-0
67. ^ P.-P. Grassé, La reconstruction du nid et les coordinations inter-individuelles chez Belicositermes natalensis et Cubitermes sp. La théorie de la Stigmergie : Essai d’interprétation du comportement des termites constructeurs, Insectes Sociaux, numéro 6, p. 41-80, 1959.
68. ^ J.L. Denebourg, J.M. Pasteels et J.C. Verhaeghe, Probabilistic Behaviour in Ants : a Strategy of Errors?, Journal of Theoretical Biology, numéro 105, 1983.
69. ^ F. Moyson, B. Manderick, The collective behaviour of Ants : an Example of Self-Organization in Massive Parallelism, Actes de AAAI Spring Symposium on Parallel Models of Intelligence, Stanford, Californie, 1988.
70. ^ M. Ebling, M. Di Loreto, M. Presley, F. Wieland, et D. Jefferson,An Ant Foraging Model Implemented on the Time Warp Operating System, Proceedings of the SCS Multiconference on Distributed Simulation, 1989
71. ^ Dorigo M., V. Maniezzo et A. Colorni, Positive feedback as a search strategy, rapport technique numéro 91-016, Dip. Elettronica, Politecnico di Milano, Italy, 1991
72. ^ R. Schoonderwoerd, O. Holland, J. Bruten et L. Rothkrantz, Ant-based load balancing in telecommunication networks, Adaptive Behaviour, volume 5, numéro 2, pages 169-207, 1997
73. ^ M. Dorigo, ANTS’ 98, From Ant Colonies to Artificial Ants : First International Workshop on Ant Colony Optimization, ANTS 98, Bruxelles, Belgique, octobre 1998.
74. ^ T. Stützle, Parallelization Strategies for Ant Colony Optimization, Proceedings of PPSN-V, Fifth International Conference on Parallel Problem Solving from Nature, Springer-Verlag, volume 1498, pages 722-731, 1998.
75. ^ É. Bonabeau, M. Dorigo et G. Theraulaz, Swarm intelligence, Oxford University Press, 1999.
76. ^ M. Dorigo , G. Di Caro et T. Stützle, Special issue on "Ant Algorithms", Future Generation Computer Systems, volume 16, numéro 8, 2000
77. ^ W.J. Gutjahr, A graph-based Ant System and its convergence, Future Generation Computer Systems, volume 16, pages 873-888, 2000.
78. ^ S. Iredi, D. Merkle et M. Middendorf, Bi-Criterion Optimization with Multi Colony Ant Algorithms, Evolutionary Multi-Criterion Optimization, First International Conference (EMO’01), Zurich, Springer Verlag, pages 359-372, 2001.
79. ^ L. Bianchi, L.M. Gambardella et M.Dorigo, An ant colony optimization approach to the probabilistic traveling salesman problem, PPSN-VII, Seventh International Conference on Parallel Problem Solving from Nature, Lecture Notes in Computer Science, Springer Verlag, Berlin, Allemagne, 2002.

Publications (selected)

• M. Dorigo, 1992. Optimization, Learning and Natural Algorithms, PhD thesis, Politecnico di Milano, Italy.
• M. Dorigo, V. Maniezzo & A. Colorni, 1996. "Ant System: Optimization by a Colony of Cooperating Agents", IEEE Transactions on Systems, Man, and Cybernetics–Part B, 26 (1): 29–41.
• M. Dorigo & L. M. Gambardella, 1997. "Ant Colony System: A Cooperative Learning Approach to the Traveling Salesman Problem". IEEE Transactions on Evolutionary Computation, 1 (1): 53–66.
• M. Dorigo, G. Di Caro & L. M. Gambardella, 1999. "Ant Algorithms for Discrete Optimization". Artificial Life, 5 (2): 137–172.
• S. Ghosh, M. Dorigo et G. Theraulaz, 1999. Swarm Intelligence: From Natural to Artificial Systems, Oxford University Press. ISBN 0-19-513159-2
• M. Dorigo & T. Stützle, 2004. Ant Colony Optimization, MIT Press. ISBN 0-262-04219-3
• M. Dorigo, 2007. "Ant Colony Optimization". Scholarpedia.
• C. Blum, 2005 "Ant colony optimization: Introduction and recent trends". Physics of Life Reviews, 2: 353-373
• M. Dorigo, M. Birattari & T. Stützle, 2006 Ant Colony Optimization: Artificial Ants as a Computational Intelligence Technique. TR/IRIDIA/2006-023
• Mohd Murtadha Mohamad,"Articulated Robots Motion Planning Using Foraging Ant Strategy",Journal of Information Technology - Special Issues in Artificial Intelligence, Vol.20, No. 4 pp. 163–181, December 2008, ISSN0128-3790.
• N. Monmarché, F. Guinand & P. Siarry (eds), "Artificial Ants", August 2010 Hardback 576 pp. ISBN 9781848211940.

External links

• Ant Colony Optimization Home Page
• AntSim - Simulation of Ant Colony Algorithms
• MIDACO-Solver General purpose optimization software based on Ant Colony Optimization (Matlab, Excel, C/C++, Fortran, Python)
• University of Kaiserslautern, Germany, AG Wehn: Ant Colony Optimization Applet Visualization of Traveling Salesman solved by Ant System with numerous options and parameters (Java Applet)
• Ant Farm Simulator