Steiner tree problem

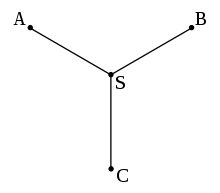Steiner tree for three points A, B, and C (note there are no direct connections between A, B, C). The Steiner point S is located at the Fermat point of the triangle ABC.

Solution for four points—note that there are two Steiner points, S₁ and S₂

The Steiner tree problem, or the minimum Steiner tree problem, named after Jakob Steiner, is a problem in combinatorial optimization, which may be formulated in a number of settings, with the common part being that it is required to find the shortest interconnect for a given set of objects.

The Steiner tree problem is superficially similar to the minimum spanning tree problem: given a set V of points (vertices), interconnect them by a network (graph) of shortest length, where the length is the sum of the lengths of all edges. The difference between the Steiner tree problem and the minimum spanning tree problem is that, in the Steiner tree problem, extra intermediate vertices and edges may be added to the graph in order to reduce the length of the spanning tree. These new vertices introduced to decrease the total length of connection are known as Steiner points or Steiner vertices. It has been proved that the resulting connection is a tree, known as the Steiner tree. There may be several Steiner trees for a given set of initial vertices.

The Steiner tree problem has applications in circuit layout or network design. Most versions of the Steiner tree problem are NP-complete. In fact, one of these was among Karp's original 21 NP-complete problems. Some restricted cases can be solved in polynomial time. In practice, heuristics are used.

Euclidean Steiner tree

The original problem was stated in the form that has become known as the Euclidean Steiner tree problem or geometric Steiner tree problem: Given N points in the plane, the goal is to connect them by lines of minimum total length in such a way that any two points may be interconnected by line segments either directly or via other points and line segments.

It may be shown that the connecting line segments do not intersect each other except at the endpoints and form a tree, hence the name of the problem.

For the Euclidean Steiner problem, points added to the graph (Steiner points) must have a degree of three, and the three edges incident to such a point must form three 120 degree angles^{[citation needed]}. It follows that the maximum number of Steiner points that a Steiner tree can have is N − 2, where N is the initial number of given points.

For N = 3, solution is given by a Steiner point located at the Fermat point of the triangle formed by the given points.

For general N, the Euclidean Steiner tree problem is NP-hard, and hence it is not known whether an optimal solution can be found by using a polynomial-time algorithm. However, there is a polynomial-time approximation scheme (PTAS) for Euclidean Steiner trees, i.e., a near-optimal solution can be found in polynomial time.^[1]

Rectilinear Steiner tree

Main article: Rectilinear Steiner tree

The minimum rectilinear Steiner tree problem (MRST) is a variant of the geometric Steiner tree problem in the plane, in which the Euclidean distance is replaced with the rectilinear distance. The problem arises in the physical design of electronic design automation. In VLSI circuits, wire routing is carried out by wires running only in vertical and horizontal directions, due to high computational complexity of the task.^[2]

Generalization of minimum spanning tree

Steiner trees have also been studied in the context of weighted graphs. In the general Steiner tree problem (Steiner tree in graphs), we are given an edge-weighted graph G = (V, E, w) and a subset S ⊆ V of required vertices. A Steiner tree is a tree in G that spans all vertices of S. There are two versions of the problem: in the optimization problem associated with Steiner trees, the task is to find a minimum-weight Steiner tree; in the decision problem, we are given a value k and the task is to determine whether a Steiner tree of total weight at most k exists. The decision problem was one of Karp's 21 NP-complete problems; hence the optimization problem is NP-hard.

A special case of this problem is when G is a complete graph, each vertex v ∈ V corresponds to a point in a metric space, and the edge weights w(e) for each e ∈ E correspond to distances in the space. Put otherwise, the edge weights satisfy the triangle inequality. This variant is known as the metric Steiner tree problem. Given an instance of the (non-metric) Steiner tree problem, we can transform it in polynomial time into an equivalent instance of the metric Steiner tree problem; the transformation preserves the approximation factor.^[3]

While the Euclidean version admits a PTAS, it is known that the metric Steiner tree problem is APX-complete, i.e., it is believed that arbitrarily good approximation ratios cannot in general be achieved in polynomial time. There is a polynomial-time algorithm that finds a factor 1.55 approximation of a minimum Steiner tree.^[4]

In a special case of the graph problem, the Steiner tree problem for quasi-bipartite graphs, S is required to include at least one endpoint of every edge in G.

The Steiner tree problem has also been investigated in higher dimensions and on various surfaces. Algorithms to find the Steiner minimal tree have been found on the sphere, torus, projective plane, wide and narrow cones, and others.^[5]

Another generalizations of the Steiner tree problem are the k-edge-connected Steiner network problem and the k-vertex-connected Steiner network problem, where the goal is to find a k-edge-connected graph or a k-vertex-connected graph rather than any connected graph.

Steiner ratio

A minimum spanning tree is a feasible but not usually optimal solution to the Steiner tree problem. The Steiner ratio is the largest possible ratio between the total length of a minimum spanning tree and the total length of a minimum Steiner tree.^[6]

In the metric Steiner tree problems, the Steiner ratio is 2. Therefore an algorithm that finds a minimum spanning tree is a polynomial-time factor-2 approximation algorithm for the metric Steiner tree problem.

In the Euclidean Steiner tree problem, the Steiner ratio is conjectured to be $\frac{2}{\sqrt{3}}$. Despite earlier claims of a proof, the conjecture is still open.^[7]

Notes

1. ^ Crescenzi, Pierluigi; Kann, Viggo; Halldórsson, Magnús; Karpinski, Marek; Woeginger, Gerhard (2000), "Minimum geometric Steiner tree", A Compendium of NP Optimization Problems, http://www.nada.kth.se/~viggo/wwwcompendium/node79.html .
2. ^ Naveed Sherwani, "Algorithms for VLSI Physical Design Automation"
3. ^ Vazirani 2003, pp. 27–28.
4. ^ Crescenzi, Pierluigi; Kann, Viggo; Halldórsson, Magnús; Karpinski, Marek; Woeginger, Gerhard (2000), "Minimum Steiner tree", A Compendium of NP Optimization Problems, http://www.nada.kth.se/~viggo/wwwcompendium/node78.html .
5. ^ Dingzhu Du, Frank Hwang (1995). Computing in Euclidean geometry. Lecture Notes of Computing. 4 (2nd ed.). River Edge, NJ: World Scientific Publishing Co. ISBN 9810218761. , p. 361
6. ^ Ganley, Joseph L. (2004), "Steiner ratio", in Black, Paul E., Dictionary of Algorithms and Data Structures, U.S. National Institute of Standards and Technology, http://www.itl.nist.gov/div897/sqg/dads/HTML/steinerratio.html, retrieved 2009-12-16 .
7. ^ Ivanov, A.O. (2011), http://www.springerlink.com/content/4433031487u14777/, retrieved 2011-4-15 .

References

• Garey, Michael R.; Johnson, David S. (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness, W. H. Freeman, ISBN 0-7167-1045-5 , p. 208–209, problems ND12 and ND13.
• F. K. Hwang, D. S. Richards, P. Winter (1992). The Steiner Tree Problem. Annals of Discrete Mathematics. 53. North-Holland: Elsevier. ISBN 0-444-89098-X. 
• A. O. Ivanov, A. A. Tuzhilin (1994). Minimal Networks: The Steiner Problem and Its Generalizations. N.W., Boca Raton, Florida: CRC Press. ISBN 978-0849386428. 
• A. O. Ivanov, A. A. Tuzhilin (2000). Branching solutions to one-dimensional variational problems. Singapore-New Jersey-London-Hong Kong: World Scientific. ISBN 978-9810240608. 
• A. O. Ivanov, A. A. Tuzhilin (2003) (in Russian). Extreme Networks Theory. Moscow-Izhevsk: Institute of Computer Investigations. ISBN 5-93972-292-X. 
• Korte, Bernhard; Vygen, Jens (2006). "Section 20.1". Combinatorial Optimization: Theory and Algorithms (3rd ed.). Springer. ISBN 3-540-25684-9. 
• Vazirani, Vijay V. (2003). Approximation Algorithms. Berlin: Springer. ISBN 3540653678. 
• Wu, Bang Ye; Chao, Kun-Mao (2004). "Chapter 7". Spanning Trees and Optimization Problems. Chapman & Hall/CRC. ISBN 1-58488-436-3. 
• Bern, Marshall W.; Graham, Ronald L. (1989). "The Shortest-Network Problem". Scientific American 260 (1): 84–89. doi:10.1038/scientificamerican0189-84. 
• Dietmar Cieslik (1998). Steiner Minimal Trees. pp. 319. ISBN 0792349830. 

External links

• Hazewinkel, M. (2001), "Steiner tree problem", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Springer, ISBN 978-1556080104, http://eom.springer.de/s/s110270.htm 
• GeoSteiner (Steiner tree solver, Source available, for non commercial use)
• http://www.archive.org/details/RonaldLG1988 (Movie: Ronald L Graham: The Shortest Network Problem (1988)
• Fortran subroutine for finding the Steiner vertex of a triangle (i.e., Fermat point), its distances from the triangle vertices, and the relative vertex weights.
• Phylomurka (Solver for the Steiner tree problem in networks)