- Circle packing
-
- This article describes the packing of circles on surfaces. For the related article on circle packing with a prescribed intersection graph, please see the circle packing theorem.
In geometry, circle packing is the study of the arrangement of circles (of equal or varying sizes) on a given surface such that no overlapping occurs and so that all circles touch another. The associated "packing density", η of an arrangement is the proportion of the surface covered by the circles. Generalisations can be made to higher dimensions – this is called sphere packing, which usually deals only with identical spheres.
The branch of mathematics generally known as "circle packing", however, is not overly concerned with dense packing of equal-sized circles (the densest packing is known) but with the geometry and combinatorics of packings of arbitrarily-sized circles: these give rise to discrete analogs of conformal mapping, Riemann surfaces and the like.
While the circle has a relatively low maximum packing density, it does not have the lowest possible. The "worst" shape to pack onto a plane is not known, but the smoothed octagon has a packing density of about 0.902414, which is the lowest maximum packing density known of any centrally-symmetric convex shape.[1] Packing densities of concave shapes such as star polygons can be arbitrarily small.
Contents
Packings in the plane
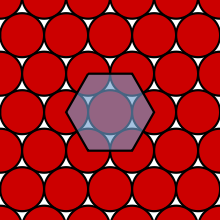
In two dimensional Euclidean space, Joseph Louis Lagrange proved in 1773 that the lattice arrangement of circles with the highest density is the hexagonal packing arrangement,[2] in which the centres of the circles are arranged in a hexagonal lattice (staggered rows, like a honeycomb), and each circle is surrounded by 6 other circles. The density of this arrangement is
Axel Thue provided the first proof that this was optimal in 1890, showing that the hexagonal lattice is the densest of all possible circle packings, both regular and irregular. However, his proof was considered by some to be incomplete. The first rigorous proof is attributed to László Fejes Tóth in 1940.[2]
At the other extreme, very low density arrangements of rigidly packed circles have been identified.
Packings on the sphere
A related problem is to determine the lowest-energy arrangement of identically interacting points that are constrained to lie within a given surface. The Thomson problem deals with the lowest energy distribution of identical electric charges on the surface of a sphere. The Tammes problem is a generalisation of this, dealing with maximising the minimum distance between circles on sphere. This is analogous to distributing non-point charges on a sphere.
Packings in bounded areas
 Fifteen equal circles packed within the smallest possible square. Only four equilateral triangles are formed by adjacent circles.
Fifteen equal circles packed within the smallest possible square. Only four equilateral triangles are formed by adjacent circles.
Packing circles in simple bounded shapes is a common type of problem in recreational mathematics. The influence of the container walls is important, and hexagonal packing is generally not optimal for small numbers of circles.
Unequal circles
There are also a range of problems which permit the sizes of the circles to be non-uniform. One such extension is to find the maximum possible density of a system with two specific sizes of circle (a binary system). Only nine particular radius ratios permit compact packing, which is when every pair of circles in contact is in mutual contact with two other circles (when line segments are drawn from contacting circle-center to circle-center, they triangulate the surface).[3]
See also
Bibliography
- Wells D (1991). The Penguin Dictionary of Curious and Interesting Geometry. New York: Penguin Books. pp. 30–31, 167. ISBN 0-14-011813-6.
References
- ^ Weisstein, Eric W., "Smoothed Octagon" from MathWorld.
- ^ a b Chang, Hai-Chau; Wang, Lih-Chung (2010). "A Simple Proof of Thue's Theorem on Circle Packing". arXiv:1009.4322v1 [math.MG].
- ^ Tom Kennedy (2006). "Compact packings of the plane with two sizes of discs". Discrete and Computational Geometry 35 (2): 255–267. arXiv:math/0407145v2. doi:10.1007/s00454-005-1172-4.
Categories:
Wikimedia Foundation. 2010.