Malfatti circles

Malfatti circles

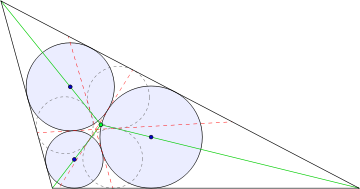
In geometry, the Malfatti circles are three circles inside a given triangle such that each circle is tangent to the other two and to two sides of the triangle. They are named after Gian Francesco Malfatti, who made early studies of the problem of constructing these circles in the mistaken belief that they would have the largest possible total area of any three disjoint circles within the triangle. Malfatti's problem has been used to refer both to the problem of constructing the Malfatti circles and to the problem of finding three area-maximizing circles within a triangle.

Malfatti's problem

Comparison of the Malfatti circles and the three area-maximizing circles within an equilateral triangle

In 1803 Gian Francesco Malfatti posed the problem of cutting three cylindrical columns out of a rectangular wedge of marble, maximizing the total volume of the columns. He assumed, as did many others after him, that the solution to this problem was given by three tangent circles within the triangular cross-section of the wedge. That is, more abstractly, he conjectured that the three Malfatti circles have the maximum total area of any three disjoint circles within a given triangle.

Malfatti published in Italian and his work may not have been read by many in the original. It was popularised for a wider readership in French by Joseph Diaz Gergonne in the first volume of his ``Annales" (1810/11), with further discussion in the second and tenth. However, this advertisement most likely acted as a filter, as Gergonne only stated the circle-tangency problem, not the area-maximizing one.

The conjecture is wrong; Lob and Richmond (1930), who went back to the original Italian text, observed that for some triangles a larger area can be achieved by a greedy algorithm that inscribes a single circle of maximal radius within the triangle, inscribes a second circle within the largest of the three remaining corners of the triangle, and inscribes a third circle within the largest of the five remaining pieces. The difference in area for an equilateral triangle is small, just over 1%,^[1] but as Howard Eves pointed out in 1946, for an isosceles triangle with a very sharp apex, the optimal circles (stacked one atop each other above the base of the triangle) have nearly twice the area of the Malfatti circles.^[2]

Goldberg (1967) showed that, for every triangle, the Lob–Richmond procedure produces three circles with larger area than the Malfatti circles, so the Malfatti circles are never optimal. Zalgaller and Los' (1994) classified all of the different ways that a set of maximal circles can be packed within a triangle; using their classification, they proved that the greedy algorithm always finds three area-maximizing circles, and they provided a formula for determining which packing is optimal for a given triangle. In his 1997 Ph.D. thesis, Melissen^[3] conjectured more generally that, for any integer n, the greedy algorithm finds the area-maximizing set of n circles within a given triangle; the conjecture is known to be true for n ≤ 3.^[4]

History

The problem of constructing three circles tangent to each other within a triangle was posed by the 18th-century Japanese mathematician Ajima Naonobu prior to the work of Malfatti, and included in an unpublished collection of Ajima's works made a year after Ajima's death by his student Kusaka Makoto.^[5] Even earlier, the same problem was considered in a 1384 manuscript by Gilio di Cecco da Montepulciano, now in the Municipal Library of Sienna, Italy.^[6]

Since the work of Malfatti, there has been a significant amount of work on methods for constructing Malfatti's three tangent circles; Richard K. Guy writes that the literature on the problem is "extensive, widely scattered, and not always aware of itself".^[7] Notably, in 1826 Jakob Steiner presented a simple geometric construction based on bitangents; other authors have since claimed that Steiner's presentation lacked a proof, which was later supplied by Andrew Hart (1856), but Guy points to the proof scattered within two of Steiner's own papers from that time. Lob and Richmond cite solutions by C. L. Lehmus (1819), Eugène Charles Catalan (1845), J. Derousseau (1895), A. Pampuch (1904), and J. L. Coolidge (1916), all based on algebraic formulations of the problem. The algebraic solutions do not distinguish between internal and external tangencies among the circles and the given triangle; if the problem is generalized to allow tangencies of either kind, then a given triangle will have 32 different solutions^[8] and conversely a triple of mutually tangent circles will be a solution for eight different triangles.^[7] Bottema^[9] and Guy cite additional work on the problem and its generalizations by C. Adams (1846), Adolphe Quidde (1850), K. H. Schellbach (1853), Arthur Cayley (1854, 1857, 1875), Alfred Clebsch (1857), P. Simons (1874), J. Casey (1888), Rouché and Comberousse (1900), H. F. Baker (1925), L. J. Rogers (1928), Angelo Procissi (1932), Jun Naito (1975), and D. G. Rogers (2005).

Gatto and Mazotti^[10] recount an episode in 19th-century Neapolitan mathematics related to the Malfatti circles. In 1839, Vincenzo Flauti, a synthetic geometer, posed a challenge involving the solution of three geometry problems, one of which was the construction of Malfatti's circles; his intention in doing so was to show the superiority of synthetic to analytic techniques. Despite a solution being given by Fortunato Padula, a student in a rival school of analytic geometry, Flauti awarded the prize to his own student, Nicola Trudi, whose solutions Flauti had known of when he posed his challenge. More recently, the problem of constructing the Malfatti circles has been used as a test problem for computer algebra systems.^[11]

Steiner's construction

Steiner's construction of the Malfatti circles.

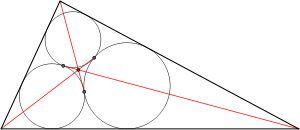
Although much of the early work on the Malfatti circles used analytic geometry, in 1826 Jakob Steiner provided the following simple synthetic construction.

A circle that is tangent to two sides of a triangle, as the Malfatti circles are, must be centered on one of the angle bisectors of the triangle (green in the figure). These bisectors partition the triangle into three smaller triangles, and Steiner's construction of the Malfatti circles begins by drawing a different triple of circles (shown dashed in the figure) inscribed within each of these three smaller triangles. Each pair of two of these three inscribed circles has two bitangents, lines that touch both of the dashed circles and pass between them: one bitangent is the angle bisector, and the second bitangent is shown as the red dashed line in the figure. Label the three sides of the given triangle as a, b, and c, and label the three bitangents that are not angle bisectors as x, y, and z, where x is the bitangent to the two circles that do not touch side a, y is the bitangent to the two circles that do not touch side b, and z is the bitangent to the two circles that do not touch side c. Then the three Malfatti circles are the inscribed circles to the three tangential quadrilaterals abyx, aczx, and bczy.^[12] The three bitangents x, y, and z cross the triangle sides at the point of tangency with the third inscribed circle, and may also be found as the reflections of the angle bisectors across the lines connecting pairs of centers of these incircles.^[7]

Radius formula

The radius of each of the three Malfatti circles may be determined as a formula involving the three side lengths a, b, and c of the triangle, the inradius r, the semiperimeter , and the three distances d, e, and f from the incenter of the triangle to the vertices opposite sides a, b, and c respectively. The formulae for the three radii are:

$r_1 = \frac{r}{2(s-a)}(s+d-r-e-f),$

$r_2 = \frac{r}{2(s-b)}(s+e-r-d-f),$ and

$r_3 = \frac{r}{2(s-c)}(s+f-r-d-e).$

According to Stevanović (2003), these formulae were discovered by Malfatti and published posthumously by him in 1811.

Related formulae may be used to find examples of triangles whose side lengths, inradii, and Malfatti radii are all rational numbers or all integers. For instance, the triangle with side lengths 28392, 21000, and 25872 has inradius 6930 and Malfatti radii 3969, 4900, and 4356. As another example, the triangle with side lengths 152460, 165000, and 190740 has inradius 47520 and Malfatti radii 27225, 30976, and 32400.^[13]

Ajima–Malfatti points

First Ajima–Malfatti point

Given a triangle ABC and its three Malfatti circles, let D, E, and F be the points where two of the circles touch each other, opposite vertices A, B, and C respectively. Then the three lines AD, BE, and CF meet in a single triangle center known as the first Ajima–Malfatti point after the contributions of Ajima and Malfatti to the circle problem. The second Ajima–Malfatti point is the meeting point of three lines connecting the tangencies of the Malfatti circles with the centers of the excircles of the triangle.^[14][15] Other triangle centers also associated with the Malfatti circles include the Yff–Malfatti point, formed in the same way as the first Malfatti point from three mutually tangent circles that are all tangent to the lines through the sides of the given triangle, but that lie partially outside the triangle,^[16] and the radical center of the three Malfatti circles.^[17]

See also

• Circle packing in an equilateral triangle
• Circle packing in an isosceles right triangle
• Six circles theorem

Notes

1. ^ Wells (1991).
2. ^ Eves (1946); Ogilvy (1990).
3. ^ Melissen, J.B.M. (1997), Packing and Covering with Circles (PhD thesis), Utrecht University .
4. ^ Andreatta, Bezdek & Boroński (2010).
5. ^ Fukagawa, Hidetoshi; Rothman, Tony (2008), Sacred mathematics: Japanese temple geometry, Princeton University Press, p. 79, ISBN 9780691127453, http://books.google.com/books?id=OxKKDCmGDlEC&pg=PA79 .
6. ^ Simi, A.; Toti Rigatelli, L. (1993), "Some 14th- and 15th-century texts on practical geometry", Vestigia mathematica, Amsterdam: Rodopi, pp. 453–470, MR1258835 .
7. ^ ^{a b c} Guy (2007).
8. ^ Bottema (2001) credits the enumeration of these solutions to Pampuch (1904), but Cajori (1893) notes that this count of the number of solutions was already given in an 1826 remark by Steiner. See Cajori, Florian (1893), A history of mathematics, Macmillan & Co., p. 296, http://books.google.com/books?id=bfgRxVzjbMYC&pg=PA296 .
9. ^ Bottema (2001).
10. ^ Mazzotti, Massimo (1998), "The geometers of God: mathematics and reaction in the kingdom of Naples", Isis 89 (4): 674–701, doi:10.1086/384160, MR1670633, http://history.berkeley.edu/faculty/Mazzotti/The%20Geometers%20of%20God.pdf . Gatto, Romano (2000), "The debate about methods and Vincenzo Flauti's challenge to the mathematicians of the Kingdom of Naples", Società Nazionale di Scienze, Lettere e Arti in Napoli. Rendiconto dell'Accademia delle Scienze Fisiche e Matematiche. Serie IV 67: 181–233, MR1834240 .
11. ^ Hitotumatu, Sin (1995), "The Malfatti problem" (in Japanese), The state of the art of scientific computing and its prospects, II, Sūrikaisekikenkyūsho Kōkyūroku, 915, pp. 167–170, MR1385273 . Takeshima, Taku; Anai, Hirokazu (1996), "Computer algebra applied to Malfatti's problem of constructing three tangent circles inside a triangle—the construction of towers over the field of rational functions" (in Japanese), Studies in the theory of computer algebra and its applications, Sūrikaisekikenkyūsho Kōkyūroku, 941, pp. 15–24, MR1410316 .
12. ^ Martin (1998), exercise 5.20, p. 96.
13. ^ Miller, W. J. C., ed. (1875), "Problem 4331", Mathematical questions with their solutions, from the "Educational times", Hodgson, p. 70, http://books.google.com/books?id=7QYAAAAAQAAJ&pg=PA70 . Proposed by Artemas Martin; solved by the proposer and by Asher B. Evans.
14. ^ Weisstein, Eric W., "Ajima-Malfatti Points" from MathWorld..
15. ^ C. Kimberling, Encyclopedia of Triangle Centers, X(179) and X(180).
16. ^ Encyclopedia of Triangle Centers, X(400).
17. ^ Stevanović (2003).

References

• Andreatta, Marco; Bezdek, András; Boroński, Jan P. (2010), "The problem of Malfatti: two centuries of debate", The Mathematical Intelligencer 33 (1): 72–76, doi:10.1007/s00283-010-9154-7, http://alpha.science.unitn.it/~andreatt/Malfatti.pdf .
• Andreescu, Titu; Mushkarov, Oleg; Stoyanov, Luchezar N. (2006), "2.3 Malfatti's Problems", Geometric problems on maxima and minima, Springer-Verlag, pp. 80–87, ISBN 9780817635176, http://books.google.com/books?id=Gvrr-7wt__gC&pg=PA80 .
• Bottema, Oene (2001), "The Malfatti problem", Forum Geometricorum 1: 43–50, MR1891514, http://forumgeom.fau.edu/FG2001volume1/FG200107.pdf .
• Dörrie, H. (1965), "§30. Malfatti's Problem", 100 Great Problems of Elementary Mathematics: Their History and Solutions, New York: Dover, pp. 147–151, ISBN 0-486-61348-8, http://books.google.com/books?id=i4SJwNrYuAUC&pg=PA147 .
• Eves, Howard (1946), Malfatti Problem (problem 4145), "Problems and Solutions", American Mathematical Monthly 53 (5): 285–286, JSTOR 2305117 .
• Goldberg, M. (1967), "On the Original Malfatti Problem", Mathematics Magazine 40: 241–247, JSTOR 2688277, MR1571715 .
• Guy, Richard K. (2007), "The lighthouse theorem, Morley & Malfatti—a budget of paradoxes", American Mathematical Monthly 114 (2): 97–141, JSTOR 27642143, MR2290364, http://www.math.ucalgary.ca/files/publications/3414848.pdf .
• Lob, H.; Richmond, H. W. (1930), "On the Solutions of Malfatti's Problem for a Triangle", Proceedings of the London Mathematical Society, 2nd ser. 30 (1): 287–304, doi:10.1112/plms/s2-30.1.287 .
• Martin, George Edward (1998), "Malfatti's Problem", Geometric Constructions, Undergraduate Texts in Mathematics, Springer-Verlag, pp. 92–95, ISBN 9780387982762, http://books.google.com/books?id=ABLtD3IE_RQC&pg=PA92 . The cover of Martin's book features an illustration of the Malfatti circles.
• Ogilvy, C. Stanley (1990), "Malfatti's problem", Excursions in Geometry, Dover, pp. 145–147, ISBN 0-486-26530-7, http://books.google.com/books?id=B2eLvr-jiG4C&pg=PA145 .
• Stevanović, Milorad R. (2003), "Triangle centers associated with the Malfatti circles", Forum Geometricorum 3: 83–93, MR2004112, http://forumgeom.fau.edu/FG2003volume3/FG200308.pdf .
• Wells, David (1991), "Malfatti's problem", The Penguin Dictionary of Curious and Interesting Geometry, New York: Penguin Books, pp. 145–146, ISBN 0-14-011813-6 .
• Zalgaller, V.A.; Los', G.A. (1994), "The solution of Malfatti's problem", Journal of Mathematical Sciences 72 (4): 3163–3177, doi:10.1007/BF01249514 .

External links

• Weisstein, Eric W., "Malfatti Circles" from MathWorld.
• Weisstein, Eric W., "Malfatti's Problem" from MathWorld.
• Malfatti's Problem at cut-the-knot