Sudoku

Not to be confused with Sodoku.

A Sudoku puzzle...

...and its solution numbers marked in red

Sudoku (数独, sūdoku^?,  listen (help·info); English pronunciation: /suːˈdoʊkuː/ soo-doh-koo) is a logic-based,^[1][2] combinatorial^[3] number-placement puzzle. The objective is to fill a 9×9 grid with digits so that each column, each row, and each of the nine 3×3 sub-grids that compose the grid (also called "boxes", "blocks", "regions", or "sub-squares") contains all of the digits from 1 to 9. The puzzle setter provides a partially completed grid, which typically has a unique solution.

Completed puzzles are always a type of Latin square with an additional constraint on the contents of individual regions. For example, the same single integer may not appear twice in the same 9×9 playing board row or column or in any of the nine 3×3 subregions of the 9×9 playing board.^[4]

The puzzle was popularized in 1986 by the Japanese puzzle company Nikoli, under the name Sudoku, meaning single number.^[5] It became an international hit in 2005.^[6]

History

From La France newspaper, July 6, 1895

Number puzzles appeared in newspapers in the late 19th century, when French puzzle setters began experimenting with removing numbers from magic squares. Le Siècle, a Paris-based daily, published a partially completed 9×9 magic square with 3×3 sub-squares on November 19, 1892.^[7] It was not a Sudoku because it contained double-digit numbers and required arithmetic rather than logic to solve, but it shared key characteristics: each row, column and sub-square added up to the same number.

On July 6, 1895, Le Siècle's rival, La France, refined the puzzle so that it was almost a modern Sudoku. It simplified the 9×9 magic square puzzle so that each row, column and broken diagonals contained only the numbers 1–9, but did not mark the sub-squares. Although they are unmarked, each 3×3 sub-square does indeed comprise the numbers 1–9 and the additional constraint on the broken diagonals leads to only one solution.^[8]

These weekly puzzles were a feature of French newspapers such as L'Echo de Paris for about a decade but disappeared about the time of World War I.^[9]

According to Will Shortz, the modern Sudoku was most likely designed anonymously by Howard Garns, a 74-year-old retired architect and freelance puzzle constructor from Indiana, and first published in 1979 by Dell Magazines as Number Place (the earliest known examples of modern Sudoku). Garns' name was always present on the list of contributors in issues of Dell Pencil Puzzles and Word Games that included Number Place, and was always absent from issues that did not.^[10] He died in 1989 before getting a chance to see his creation as a worldwide phenomenon.^[10] It is unclear if Garns was familiar with any of the French newspapers listed above.

The puzzle was introduced in Japan by Nikoli in the paper Monthly Nikolist in April 1984^[10] as Sūji wa dokushin ni kagiru (数字は独身に限る^?), which can be translated as "the digits must be single" or "the digits are limited to one occurrence." (In Japanese,"dokushin" means an "unmarried person".) At a later date, the name was abbreviated to Sudoku(數獨) by Maki Kaji (鍜治 真起, Kaji Maki^?), taking only the first kanji of compound words to form a shorter version.^[10] In 1986, Nikoli introduced two innovations: the number of givens was restricted to no more than 32, and puzzles became "symmetrical" (meaning the givens were distributed in rotationally symmetric cells). It is now published in mainstream Japanese periodicals, such as the Asahi Shimbun.

Variants

A nonomino or Jigsaw Sudoku puzzle, as seen in the Sunday Telegraph

Solution numbers in red for above puzzle

Although the 9×9 grid with 3×3 regions is by far the most common, variations abound. Sample puzzles can be 4×4 grids with 2×2 regions; 5×5 grids with pentomino regions have been published under the name Logi-5; the World Puzzle Championship has featured a 6×6 grid with 2×3 regions and a 7×7 grid with six heptomino regions and a disjoint region. Larger grids are also possible. The Times offers a 12×12-grid Dodeka sudoku with 12 regions of 4×3 squares. Dell regularly publishes 16×16 Number Place Challenger puzzles (the 16×16 variant often uses 1 through G rather than the 0 through F used in hexadecimal). Nikoli offers 25×25 Sudoku the Giant behemoths. Sudoku-zilla,^[11] a 100x100-grid was published in print in 2010.

A Killer Sudoku puzzle

Solution for puzzle to the left

Hypersudoku puzzle

Solution numbers for puzzle to the left

A Wordoku puzzle

Solution in red for puzzle to the left

Another common variant is to add limits on the placement of numbers beyond the usual row, column, and box requirements. Often the limit takes the form of an extra "dimension"; the most common is to require the numbers in the main diagonals of the grid also to be unique. The aforementioned Number Place Challenger puzzles are all of this variant, as are the Sudoku X puzzles in the Daily Mail, which use 6×6 grids.

Mini Sudoku

A variant named "Mini Sudoku" appears in the American newspaper USA Today and elsewhere, which is played on a 6×6 grid with 3×2 regions. The object is the same as standard Sudoku, but the puzzle only uses the numbers 1 through 6.

Cross Sums Sudoku

Another variant is the combination of Sudoku with Kakuro on a 9×9 grid, called Cross Sums Sudoku, in which clues are given in terms of cross sums. The clues can also be given by cryptic alphametics in which each letter represents a single digit from 0 to 9. An excellent example is NUMBER+NUMBER=KAKURO which has a unique solution 186925+186925=373850. Another example is SUDOKU=IS*FUNNY whose solution is 426972=34*12558.

Killer Sudoku

Example of a Killer Sudoku problem

Solution to the example above

The same example problem, as it would be printed in black and white

Killer sudoku (also killer su doku, sumdoku, sum doku, addoku, or samunamupure) is a puzzle that combines elements of sudoku and kakuro. Despite the name, the simpler killer sudokus can be easier to solve than regular sudokus, depending on the solver's skill at mental arithmetic; the hardest ones, however, can take hours to crack.

History

Killer sudokus were already an established variant of sudoku in Japan by the mid 1990s, where they were known as "samunamupure." The name stemmed from a Japanized form of the English words "sum number place." Killer sudokus were introduced to most of the English-speaking world by The Times in 2005.

Traditionally, as with regular sudoku puzzles, the grid layout is symmetrical around a diagonal, horizontal or vertical axis, or a quarter or half turn about the centre. This is a matter of aesthetics, though, rather than obligatory: many Japanese puzzle-makers will make small deviations from perfect symmetry for the sake of improving the puzzle. Other puzzle-makers may produce entirely asymmetrical puzzles.

Terminology

Cell 

A single square that contains one number in the grid

Row 

A horizontal line of 9 cells

Column 

A vertical line of 9 cells

Nonet 

A 3×3 grid of cells, as outlined by the bolder lines in the diagram above

Cage 

The grouping of cells denoted by a dotted line or by individual colours.

House 

Any nonrepeating set of 9 cells: can be used as a general term for "row, column, or nonet" (or, in Killer X variants, "long diagonal")

Rules

The objective is to fill the grid with numbers from 1 to 9 in a way that the following conditions are met:

• Each row, column, and nonet contains each number exactly once.
• The sum of all numbers in a cage must match the small number printed in its corner.
• No number appears more than once in a cage. (This is the standard rule for killer sudokus, and implies that no cage can include more than 9 cells.)

In 'Killer X', an additional rule is that each of the long diagonals contains each number once.

Duplicate cell ambiguity

By convention in Japan, killer sudoku cages do not include duplicate numbers. However, when The Times first introduced the killer sudoku on 31 August 2005, the newspaper did not make this rule explicit. Even though the vast majority of killer sudoku puzzles followed the rule anyway, English-speaking solvers scratched their heads over appropriate solving strategies given the ambiguity. On September 16, 2005 The Times added a new ruling that “Within each dotted-line shape, a digit CAN be repeated if the normal row, column and 3×3 box rules are not broken”. But on September 19 the rule changed to “Within each dotted-line shape, a digit CANNOT be repeated if the normal row, column and 3×3 box rules are not broken” - causing even more scratching of heads. This revised rule stuck and the world standard^{[citation needed]} is no duplicates within cages.

Solving strategies

Fewest possible combinations

Generally the problem is best tackled starting from the extreme sums — cages with the largest or the smallest sums. This is because these have the fewest possible combinations. For example, 3 cells within the same cage totalling 23 can only be 6, 8, and 9.

In the early stages of the game, the most common way to begin filling in numbers is to look at such low-sum or high-sum cages that form a 'straight line'. As the solver can infer from these that certain numbers are in a certain row or column, he can begin 'cross-hatching' across from them.

The 45 rule

A further technique can be derived from the knowledge that the numbers in all houses (rows, columns and nonets) add up to 45. By adding up the cages and single numbers in a particular house, the user can deduce the result of a single cell. If the cell calculated is within the house itself, it is referred to as an 'innie'; conversely if the cell is outside it, it is called an 'outie'. Even if this is not possible, advanced players may find it useful to derive the sum of two or three cells, then use other elimination techniques (see below for an example of this). The '45' technique can also be extended to calculate the innies or outies of N adjacent houses, as the difference between the cage-sums and N*45.

Initial analysis of the sample problem

The sample problem

Fewest possible combinations

The two cells in the top left must be 1+2. The 3 cells to the right totaling 15 cannot therefore have either a 1 or a 2, so they must be either 3+4+8, 3+5+7, or 4+5+6.

The two vertical cells in the top left of the top right nonet cannot be 2+2 as that would mean duplicates, so they must be 1+3. The 1 cannot be in the top line as that conflicts with our first 2 cells therefore the top cell of this pair is 3 and the lower cell 1. This also means the 3 cell cage 15 to the left cannot contain a 3 and so is 4+5+6.

Similarly the neighbouring 16 must be 9+7.

The four cells in the top right cage (totaling 15) can only include one of 1, 3, 7, or 9 (if at all) because of the presence of 1, 3, 7, and 9 in the top right hand nonet. If any one of 1, 3, 7, or 9 is present then this must be the lone square in the nonet below. Therefore these 4 cells is one of 1+2+4+8 or 2+3+4+6.

The 2 cells in the middle of the left edge must be either 1+5 or 2+4. And so on.

45

Looking at the nonet on the left hand side in the middle, we can see that there are three cages which do not cross over into another nonet; these add up to 33, meaning that the sum of the remaining two cells must be 12. This does not seem particularly useful, but consider that the cell in the bottom right of the nonet is part of a 3-cage of 6; it can therefore only contain 1, 2 or 3. If it contained 1 or 2, the other cell would have to contain 11 or 10 respectively; this is impossible. It must, therefore, contain 3, and the other cell 9.

Cage total tables

The following tables list the possible combinations for various sums.

2 cells

 3: 12
 4: 13
 5: 14 23
 6: 15 24
 7: 16 25 34
 8: 17 26 35
 9: 18 27 36 45
10: 19 28 37 46
11: 29 38 47 56
12: 39 48 57
13: 49 58 67
14: 59 68 
15: 69 78
16: 79
17: 89

3 cells

 6: 123
 7: 124
 8: 125 134
 9: 126 135 234
10: 127 136 145 235
11: 128 137 146 236 245
12: 129 138 147 156 237 246 345
13: 139 148 157 238 247 256 346
14: 149 158 167 239 248 257 347 356
15: 159 168 249 258 267 348 357 456
16: 169 178 259 268 349 358 367 457
17: 179 269 278 359 368 458 467
18: 189 279 369 378 459 468 567
19: 289 379 469 478 568
20: 389 479 569 578
21: 489 579 678
22: 589 679
23: 689
24: 789

4 cells

10: 1234
11: 1235
12: 1236 1245
13: 1237 1246 1345
14: 1238 1247 1256 1346 2345
15: 1239 1248 1257 1347 1356 2346
16: 1249 1258 1267 1348 1357 1456 2347 2356
17: 1259 1268 1349 1358 1367 1457 2348 2357 2456
18: 1269 1278 1359 1368 1458 1467 2349 2358 2367 2457 3456
19: 1279 1369 1378 1459 1468 1567 2359 2368 2458 2467 3457
20: 1289 1379 1469 1478 1568 2369 2378 2459 2468 2567 3458 3467
21: 1389 1479 1569 1578 2379 2469 2478 2568 3459 3468 3567
22: 1489 1579 1678 2389 2479 2569 2578 3469 3478 3568 4567
23: 1589 1679 2489 2579 2678 3479 3569 3578 4568
24: 1689 2589 2679 3489 3579 3678 4569 4578
25: 1789 2689 3589 3679 4579 4678
26: 2789 3689 4589 4679 5678
27: 3789 4689 5679
28: 4789 5689
29: 5789
30: 6789

5 cells

15: 12345
16: 12346
17: 12347 12356
18: 12348 12357 12456
19: 12349 12358 12367 12457 13456
20: 12359 12368 12458 12467 13457 23456
21: 12369 12378 12459 12468 12567 13458 13467 23457
22: 12379 12469 12478 12568 13459 13468 13567 23458 23467
23: 12389 12479 12569 12578 13469 13478 13568 14567 23459 23468 23567
24: 12489 12579 12678 13479 13569 13578 14568 23469 23478 23568 24567
25: 12589 12679 13489 13579 13678 14569 14578 23479 23569 23578 24568 34567
26: 12689 13589 13679 14579 14678 23489 23579 23678 24569 24578 34568
27: 12789 13689 14589 14679 15678 23589 23679 24579 24678 34569 34578
28: 13789 14689 15679 23689 24589 24679 25678 34579 34678
29: 14789 15689 23789 24689 25679 34589 34679 35678
30: 15789 24789 25689 34689 35679 45678
31: 16789 25789 34789 35689 45679
32: 26789 35789 45689
33: 36789 45789
34: 46789
35: 56789

6 cells

21: 123456
22: 123457
23: 123458 123467
24: 123459 123468 123567
25: 123469 123478 123568 124567
26: 123479 123569 123578 124568 134567
27: 123489 123579 123678 124569 124578 134568 234567
28: 123589 123679 124579 124678 134569 134578 234568
29: 123689 124589 124679 125678 134579 134678 234569 234578
30: 123789 124689 125679 134589 134679 135678 234579 234678
31: 124789 125689 134689 135679 145678 234589 234679 235678
32: 125789 134789 135689 145679 234689 235679 245678
33: 126789 135789 145689 234789 235689 245679 345678
34: 136789 145789 235789 245689 345679
35: 146789 236789 245789 345689
36: 156789 246789 345789
37: 256789 346789
38: 356789
39: 456789

7 cells

28: 1234567
29: 1234568
30: 1234569 1234578
31: 1234579 1234678
32: 1234589 1234679 1235678
33: 1234689 1235679 1245678
34: 1234789 1235689 1245679 1345678
35: 1235789 1245689 1345679 2345678
36: 1236789 1245789 1345689 2345679
37: 1246789 1345789 2345689
38: 1256789 1346789 2345789
39: 1356789 2346789
40: 1456789 2356789
41: 2456789
42: 3456789

8 cells

36: 12345678
37: 12345679
38: 12345689
39: 12345789
40: 12346789
41: 12356789
42: 12456789
43: 13456789
44: 23456789

9 cells

45: 123456789

6, 7, and 8 cells

It is easiest to determine the combinations within large cages by means of complements. The table for 6 cell cages is the complement of the 3 cell table adding up to 45 minus the listed value; similarly, the 7 cell table complements the 2 cell table. An 8-cell cage is of course missing only one digit (45 minus the sum of the cage).

Photo Sudoku

Photo Sudoku is a variation that allows users to play sudoku with pictures.

Alphabetical Sudoku

Alphabetical variations have emerged, sometimes called Wordoku; there is no functional difference in the puzzle unless the letters spell something. Some variants, such as in the TV Guide, include a word reading along a main diagonal, row, or column once solved; determining the word in advance can be viewed as a solving aid. A Wordoku might contain other words, other than the main word. Like in the example to the left, the words "Kari", "Park" and "Per" could also be found in the solution. This might be avoided by e.g. substituting the character "R" with e.g. a "Q".

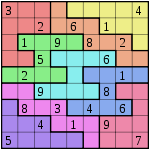
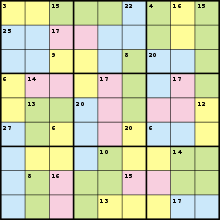
A typical problem is shown on the right, using colors to define the groups of cells. More often, puzzles are printed in black and white, with thin dotted lines used to outline the "cages" (see below for terminology).

Hypersudoku

Hypersudoku is one of the most popular variants. It is published by newspapers and magazines around the world and is also known as "NRC Sudoku", "Windoku", "Hyper-Sudoku" and "4 Square Sudoku". The layout is identical to a normal Sudoku, but with additional interior areas defined in which the numbers 1 to 9 must appear. The solving algorithm is slightly different from the normal Sudoku puzzles because of the leverage on the overlapping squares. This overlap gives the player more information to logically reduce the possibilities in the remaining squares. The approach to playing is similar to Sudoku but with possibly more emphasis on scanning the squares and overlap rather than columns and rows.

Puzzles constructed from multiple Sudoku grids are common. Five 9×9 grids which overlap at the corner regions in the shape of a quincunx is known in Japan as Gattai 5 (five merged) Sudoku. In The Times, The Age and The Sydney Morning Herald this form of puzzle is known as Samurai SuDoku. The Baltimore Sun and the Toronto Star publish a puzzle of this variant (titled High Five) in their Sunday edition. Often, no givens are to be found in overlapping regions. Sequential grids, as opposed to overlapping, are also published, with values in specific locations in grids needing to be transferred to others.

Str8ts shares the Sudoku requirement of uniqueness in the rows and columns but the third constraint is very different. Str8ts uses black cells (some with clue numbers) to divide the board into compartments. These must be filled with a set of numbers that form a 'straight', like the poker hand. A straight is a set of numbers with no gaps in them, such as '4,3,6,5' – and the order can be non-sequential. 9×9 is the traditional size but with suitable placement of black cells any size board is possible.

An example of Greater Than Sudoku

A tabletop version of Sudoku can be played with a standard 81-card Set deck (see Set game). A three-dimensional Sudoku puzzle was invented by Dion Church and published in the Daily Telegraph in May 2005. The Times also publishes a three-dimensional version under the name Tredoku. There is a Sudoku version of the Rubik's Cube named Sudoku Cube.

There are many other variants. Some are different shapes in the arrangement of overlapping 9×9 grids, such as butterfly, windmill, or flower.^[12] Others vary the logic for solving the grid. One of these is Greater Than Sudoku. In this a 3×3 grid of the Sudoku is given with 12 symbols of Greater Than (>) or Less Than (<) on the common line of the two adjacent numbers.^[10] Another variant on the logic of solution is Clueless Sudoku, in which nine 9×9 Sudoku grids are themselves placed in a three-by-three array. The center cell in each 3×3 grid of all nine puzzles is left blank and form a tenth Sudoku puzzle without any cell completed; hence, "clueless".^[12]

Mathematics of Sudoku

Main article: Mathematics of Sudoku

A completed Sudoku grid is a special type of Latin square with the additional property of no repeated values in any of the 9 blocks of contiguous 3×3 cells. The relationship between the two theories is now completely known, after Denis Berthier proved in his book The Hidden Logic of Sudoku (May 2007) that a first-order formula^{[clarification needed]} that does not mention blocks (also called boxes or regions) is valid for Sudoku if and only if it is valid for Latin Squares (this property is trivially true for the axioms and it can be extended to any formula). (Citation taken from p. 76 of the first edition: "any block-free resolution rule is already valid in the theory of Latin Squares extended to candidates" – which is restated more explicitly in the second edition, p. 86, as: "a block-free formula is valid for Sudoku if and only if it is valid for Latin Squares").

The first known calculation of the number of classic 9×9 Sudoku solution grids was posted on the USENET newsgroup rec.puzzles in September 2003^[13] and is 6,670,903,752,021,072,936,960 (sequence A107739 in OEIS), or approximately 6.67 x 10²¹. This is roughly 1.2×10⁻⁶ times the number of 9×9 Latin squares. A detailed calculation of this figure was provided by Bertram Felgenhauer and Frazer Jarvis in 2005.^[14] Various other grid sizes have also been enumerated—see the main article for details. The number of essentially different solutions, when symmetries such as rotation, reflection, permutation and relabelling are taken into account, was shown by Ed Russell and Frazer Jarvis to be just 5,472,730,538^[15] (sequence A109741 in OEIS).

The maximum number of givens provided while still not rendering a unique solution is four short of a full grid; if two instances of two numbers each are missing and the cells they are to occupy form the corners of an orthogonal rectangle, and exactly two of these cells are within one region, there are two ways the numbers can be assigned. Since this applies to Latin squares in general, most variants of Sudoku have the same maximum. The inverse problem—the fewest givens that render a solution unique—is unsolved, although the lowest number yet found for the standard variation without a symmetry constraint is 17, a number of which have been found by Japanese puzzle enthusiasts,^[16][17] and 18 with the givens in rotationally symmetric cells. Over 48,000 examples of Sudokus with 17 givens resulting in a unique solution are known.

Early in 2009, Puerto Rican mathematician Francisco Javier Rodriguez, lead researcher at the Centro Chaguin de Investigación Matematicas y Filosoficas in Mayaguez, discovered a variation, called Sudoku de Calne, based on the conbíf algorithm.^{[citation needed]}

In 2010 mathematicians Paul Newton and Stephen DeSalvo of the University of Southern California showed that the arrangement of numbers in Sudoku puzzles are more random than the number arrangements in randomly generated 9x9 matrices. This is because the rules of Sudoku exclude some random arrangements that have an innate symmetry.^[18]

Recent popularity

In 1997, New Zealander and retired Hong Kong judge Wayne Gould, then in his early 50s, saw a partly completed puzzle in a Japanese bookshop. Over six years he developed a computer program to produce puzzles quickly. Knowing that British newspapers have a long history of publishing crosswords and other puzzles, he promoted Sudoku to The Times in Britain, which launched it on 12 November 2004 (calling it Su Doku). The first letter to The Times regarding Su Doku was published the following day on 13 November from Ian Payn of Brentford, complaining that the puzzle had caused him to miss his stop on the tube.^[19]

The rapid rise of Sudoku in Britain from relative obscurity to a front-page feature in national newspapers attracted commentary in the media and parody (such as when The Guardian's G2 section advertised itself as the first newspaper supplement with a Sudoku grid on every page).^[20] Recognizing the different psychological appeals of easy and difficult puzzles, The Times introduced both side by side on 20 June 2005. From July 2005, Channel 4 included a daily Sudoku game in their Teletext service. On 2 August, the BBC's programme guide Radio Times featured a weekly Super Sudoku which features a 16×16 grid.

In the United States, the first newspaper to publish a Sudoku puzzle by Wayne Gould was The Conway Daily Sun (New Hampshire), in 2004.^[21]

The world's first live TV Sudoku show, 1 July 2005, Sky One

The world's first live TV Sudoku show, Sudoku Live, was a puzzle contest first broadcast on 1 July 2005 on Sky One. It was presented by Carol Vorderman. Nine teams of nine players (with one celebrity in each team) representing geographical regions competed to solve a puzzle. Each player had a hand-held device for entering numbers corresponding to answers for four cells. Phil Kollin of Winchelsea, England was the series grand prize winner taking home over £23,000 over a series of games. The audience at home was in a separate interactive competition, which was won by Hannah Withey of Cheshire.

Later in 2005, the BBC launched SUDO-Q, a game show that combines Sudoku with general knowledge. However, it uses only 4×4 and 6×6 puzzles. Four seasons were produced, before the show ended in 2007.

In 2006, a Sudoku website published songwriter Peter Levy's Sudoku tribute song,^[22] but quickly had to take down the mp3 due to heavy traffic. British and Australian radio picked up the song, which is to feature in a British-made Sudoku documentary. The Japanese Embassy also nominated the song for an award, with Levy doing talks with Sony in Japan to release the song as a single.^[23]

Sudoku software is very popular on PCs, websites, and mobile phones. It comes with many distributions of Linux. Software has also been released on video game consoles, such as the Nintendo DS, PlayStation Portable, the Game Boy Advance, Xbox Live Arcade, the Nook e-book reader, several iPod models, and the iPhone. In fact, just two weeks after Apple Inc. debuted the online App Store within its iTunes store on July 11, 2008, there were already nearly 30 different Sudoku games, created by various software developers, specifically for the iPhone and iPod Touch. One of the most popular video games featuring Sudoku is Brain Age: Train Your Brain in Minutes a Day!. Critically and commercially well received, it generated particular praise for its Sudoku implementation^[24][25][26] and sold more than 8 million copies worldwide.^[27] Due to its popularity, Nintendo made a second Brain Age game titled Brain Age², which has over 100 new Sudoku puzzles and other activities.

In June 2008 an Australian drugs-related jury trial costing over A$1,000,000 was aborted when it was discovered that five of the twelve jurors had been playing Sudoku instead of listening to evidence.^[28]

Competitions

• The first World Sudoku Championship was held in Lucca, Italy, from March 10–12, 2006. The winner was Jana Tylová of the Czech Republic.^[29] The competition included numerous variants.^[30]
• The second World Sudoku Championship was held in Prague from March 28 to April 1, 2007.^[31] The individual champion was Thomas Snyder of the USA. The team champion was Japan.^[32]
• The third World Sudoku Championship was held in Goa, India, from April 14–16, 2008. Thomas Snyder repeated as the individual overall champion, and also won the first ever Classic Trophy (a subset of the competition counting only classic Sudoku). The Czech Republic won the team competition.^[33]
• The fourth World Sudoku Championship was held in Žilina, Slovakia, from April 24–27, 2009. After past champion Thomas Snyder of USA won the general qualification, Jan Mrozowski of Poland emerged from a 36-competitor playoff to become the new World Sudoku Champion. Host nation Slovakia emerged as the top team in a separate competition of three-membered squads.^[34]
• The fifth World Sudoku Championship was held in Philadelphia, USA from April 29 – May 2, 2010. Jan Mrozowski of Poland successfully defended his world title in the individual competition while Germany won a separate team event. The puzzles were written by Thomas Snyder and Wei-Hwa Huang, both past US Sudoku champions.^[35]
• In the United States, The Philadelphia Inquirer Sudoku National Championship has been held three times, each time offering a $10,000 prize to the advanced division winner and a spot on the U.S. National Sudoku Team traveling to the world championships. Puzzlemaster Will Shortz has served as tournament host. The winners of the event have been Thomas Snyder (2007),^[36] Wei-Hwa Huang (2008), and Tammy McLeod (2009).^[37] In the most recent event, the third place finalist in the advanced division, Eugene Varshavsky, performed quite poorly onstage after setting a very fast qualifying time on paper, which caught the attention of organizers and competitors including past champion Thomas Snyder who requested organizers reconsider his results due to a suspicion of cheating.^[38] Following an investigation and a retest of Varshavsky, the organizers disqualified him and awarded Chris Narrikkattu third place.^[39]

See also

• 36 cube
• Algorithmics of Sudoku
• Futoshiki
• Hidato
• Kakuro
• KenKen
• List of Nikoli puzzle types
• List of Sudoku terms and jargon
• Logic puzzle
• Mathematics of Sudoku
• Nonogram (aka Paint by numbers, O'ekaki)
• Str8ts sequential numbers

Notes

1. ^ Arnoldy, Ben. "Sudoku Strategies". The Home Forum (The Christian Science Monitor). 
2. ^ Schaschek, Sarah (March 22, 2006). "Sudoku champ's surprise victory". The Prague Post. Archived from the original on August 13, 2006. http://web.archive.org/web/20060813145953/http://www.praguepost.com/P03/2006/Art/0323/news5.php. Retrieved February 18, 2009. 
3. ^ Lawler, E.L.; Jan Karel Lenstra, A. H. G. Rinnooy Kan, D. B. Shmoys (1985). The Traveling Salesman problem – A Guided Tour of Combinatorial Optimization. John Wiley & Sons. ISBN 0471904139. 
4. ^ Sudoku.name
5. ^ Brian Hayes (2006). Unwed Numbers. 94. American Scientist. pp. 12–15. 
6. ^ So you thought Sudoku came from the Land of the Rising Sun ... The puzzle gripping the nation actually began at a small New York magazine by David Smith The Observer, Sunday May 15, 2005 Accessed June 13, 2008
7. ^ Boyer, Christian (May 2006). "Supplément de l’article « Les ancêtres français du sudoku »" (PDF). Pour la Science: 1–6. Archived from the original on December 10, 2006. http://web.archive.org/web/20061210103525/http://cboyer.club.fr/multimagie/SupplAncetresSudoku.pdf. Retrieved 3 August 2009. 
8. ^ Boyer, Christian (2007). "Sudoku's French ancestors". Archived from the original on October 10, 2007. http://web.archive.org/web/20071010081626/http://cboyer.club.fr/multimagie/English/SudokuAncestors.htm. Retrieved 3 August 2009. 
9. ^ Malvern, Jack (2006-06-03). "Les fiendish French beat us to Su Doku". Times Online (London). http://www.timesonline.co.uk/article/0,,2-2208881,00.html. Retrieved 2006-09-16. 
10. ^ ^{a b c d e} Pegg, Ed, Jr. (2005-09-15). "Ed Pegg Jr.'s Math Games: Sudoku Variations". MAA Online. The Mathematical Association of America. http://www.maa.org/editorial/mathgames/mathgames_09_05_05.html. Retrieved October 3, 2006. 
11. ^ Eisenhauer, William (2010). Sudoku-zilla. CreateSpace. pp. 220. ISBN 978-1-45-151049-2. 
12. ^ ^{a b} "www.janko.at". http://www.janko.at/Raetsel/Zahlenraetsel.htm. 
13. ^ "Combinatorial question on 9×9". Google newsgroups archive. http://groups.google.co.uk/group/rec.puzzles/browse_thread/thread/3ba62ed2d76a052/94ce2b94b84f4e53?lnk=st&q=6670903752021072936960++#94ce2b94b84f4e53. Retrieved September 2003. 
14. ^ Jarvis, Frazer (2006-07-31). "Sudoku enumeration problems". Frazer Jarvis's home page. http://www.afjarvis.staff.shef.ac.uk/sudoku/. Retrieved September 16, 2006. 
15. ^ Jarvis, Frazer; Ed Russell (2005-09-07). "There are 5472730538 essentially different Sudoku grids ... and the Sudoku symmetry group". Frazer Jarvis's home page. http://www.afjarvis.staff.shef.ac.uk/sudoku/sudgroup.html. Retrieved September 16, 2006. 
16. ^ "プログラミングパズルに関心のある人は雑談しましょう" (in Japanese). プログラミングパズル雑談コーナー / Programming Puzzle Idle Talk Corner. http://www2.ic-net.or.jp/~takaken/auto/guest/bbs46.html. Retrieved September 16, 2006. 
17. ^ Royle, Gordon. "Minimum Sudoku". http://www.csse.uwa.edu.au/~gordon/sudokumin.php. Retrieved September 16, 2006. 
18. ^ Paul K. Newton and Stephen A. DeSalvo. The Shannon entropy of Sudoku matrices Proceedings of the Royal Society A. doi: 10.1098/rspa.2009.0522.
19. ^ Timesonline.co.uk
20. ^ "G2, home of the discerning Sudoku addict". The Guardian (London: Guardian Newspapers Limited). 2005-05-13. http://www.guardian.co.uk/g2/story/0,,1482817,00.html. Retrieved 2006-09-16. 
21. ^ Correction attached to "Inside Japan’s Puzzle Palace", New York Times, March 21, 2007
22. ^ "Sudoku the song, by Peter Levy". Sudoku.org.uk. 2006-08-17. http://www.sudoku.org.uk/news.htm. Retrieved 2008-10-05. 
23. ^ "Hit Song Has the Numbers". The Herald Sun. 2006-08-17. http://www.news.com.au/heraldsun/story/0,21985,20152238-28957,00.html. Retrieved 2008-10-05. ^{[dead link]}
24. ^ Gamerankings.com
25. ^ Gamespot.com
26. ^ IGN.com
27. ^ Gamespot.com
28. ^ Knox, Malcolm (2008-06-11). "The game's up: jurors playing Sudoku abort trial". The Sydney Morning Herald. http://www.smh.com.au/news/national/jurors-get-1-million-trial-aborted/2008/06/10/1212863636766.html. Retrieved 2008-06-11. 
29. ^ "Sudoku title for Czech accountant" (Free). BBC NEWS. 2006-03-11. http://news.bbc.co.uk/1/hi/world/europe/4797540.stm. Retrieved 2006-09-11. 
30. ^ "World Sudoku Championship 2006 Instructions Booklet" (PDF). BBC News. http://news.bbc.co.uk/2/shared/bsp/hi/pdfs/10_03_06_sudoku.pdf. Retrieved 2010-05-24. 
31. ^ "Report on the 8th General Assembly of the World Puzzle Federation" (Free). WPF. 2006-10-30. http://www.worldpuzzle.org/championships/2006/report.html. Retrieved 2006-11-15. 
32. ^ "Thomas Snyder wins World Sudoku Championship". US Puzzle Team. 2007-03-31. http://wpc.puzzles.com/press/index.htm#2007-2. Retrieved 2008-04-18. 
33. ^ Harvey, Michael (2008-04-17). "It’s a puzzle but sun, sea and beer can’t compete with Sudoku for British team". TimesOnline (London). http://entertainment.timesonline.co.uk/tol/arts_and_entertainment/games_and_puzzles/article3761511.ece. Retrieved 2008-04-18. 
34. ^ Malvern, Jack (2009-04-27). "Su Doku battle goes a little off the wall". TimesOnline (London). http://entertainment.timesonline.co.uk/tol/arts_and_entertainment/games_and_puzzles/sudoku/article6175809.ece. Retrieved 2009-04-27. 
35. ^ "Pole, 23, repeats as Sudoku world champ". PhillyInquirer. 2009-05-02. http://www.philly.com/philly/news/local/92606119.html. Retrieved 2009-05-03. ^{[dead link]}
36. ^ "Thomas Snyder, World Sudoku champion" (Free). Philadelphia Inquirer. 2007-10-21. http://www.philly.com/philly/comics_games/sudoku/Thomas_Snyder__World_Sudoku_champion.html. Retrieved 2007-10-21. 
37. ^ "Going for 2d, she wins 1st" (Free). Philadelphia Inquirer. 2009-10-25. http://www.philly.com/philly/news/local/65922787.html. Retrieved 2009-10-27. ^{[dead link]}
38. ^ "Possible cheating probed at Sudoku National Championship" (Free). Philadelphia Inquirer. 2009-10-27. http://www.philly.com/inquirer/local/20091027_Possible_cheating_probed_at_Sudoku_tournament.html. Retrieved 2009-10-27. ^{[dead link]}
39. ^ "3rd-place winner disqualified in sudoku scandal" (Free). Philadelphia Inquirer. 2009-11-24. http://www.philly.com/philly/news/local/20091124_3d-place_winner_disqualified_in_Sudoku_scandal.html. Retrieved 2009-11-24. ^{[dead link]}

Further reading

• Delahaye, Jean-Paul, "The Science Behind Sudoku", Scientific American magazine, June 2006.
• Kim, Scott, "The Science of Sudoku", 2006
• Provan, J. Scott, "Sudoku: Strategy Versus Structure", American Mathematical Monthly, October 2009. Published also as a University of North Carolina technical report UNC/STOR/08/04, 2008.

External links

• Sudoku at the Open Directory Project – An active listing of Sudoku links.
• 'Father of Sudoku' puzzles next move BBC