Chamberlin trimetric projection

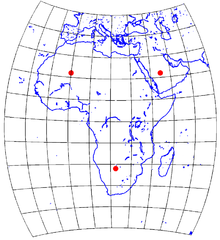A map of Africa using the Chamberlin trimetric projection. The three red dots indicate the selected "base" locations: (22°N, 0°), (22°N, 45°E), (22°S, 22.5°E). 10° graticule.

The Chamberlin trimetric projection is a map projection where three points are fixed on the globe and the points on the sphere are mapped onto a plane by triangulation. It was developed in 1946 by Wellman Chamberlin for the National Geographic Society.^[1] Chamberlin was chief cartographer for the Society from 1964 to 1971.^[2] The projection's principal feature is that it compromises between distortions of area, direction, and distance. A Chamberlin trimetric map therefore gives an excellent overall sense of the area being mapped.^[3] National Geographic Society maps have often used this projection for representations of many of the continents.^[2]

As originally implemented, the projection algorithm begins with the selection of three points near the outer boundary of the area to be mapped. From these three base points, the true distances to a point on the mapping area are calculated. The distances from each of the three base points are then drawn on the plane by compass circles. Unlike triangulation on a plane where three such compass circles will intersect at a unique point, the compass circles from a sphere do not intersect precisely at a point. A small triangle is generated from the intersections, and the center of this triangle is calculated as the mapped point.^[1]

A Chamberlin trimetric projection map was originally obtained by graphically mapping points at regular intervals of latitude and longitude, with shorelines and other features then mapped by interpolation. Based on the principles of the projection, precise, but lengthy, mathematical formulas were later developed for calculating this projection by computer for a spherical earth.^[2][3][4]

The Chamberlin trimetric projection is not equidistant, not conformal, inequivalent, and not azimuthal. Rather, the projection strikes a balanced compromise between each of these distortions.^[3] This projection is not appropriate for mapping the entire sphere.

See also

• Two-point equidistant projection

References

1. ^ ^{a b} Chamberlin, Wellman (1947). The Round Earth on Flat Paper: Map Projections Used by Cartographers. Washington, D.C.: National Geographic Society. ASIN B000WTCPXE. 
2. ^ ^{a b c} Snyder, John P. (1997). Flattening the earth: two thousand years of map projections. University of Chicago Press. ISBN 9780226767475. 
3. ^ ^{a b c} Christensen, Albert H.J. (1992). "The Chamberlin Trimetric Projection". 19. Cartography and Geographic Information Science. pp. 88–100. http://www.ingentaconnect.com/content/acsm/cagis/1992/00000019/00000002/art00003. Retrieved 2009-12-19. 
4. ^ Bretterbauer, Kurt (1989). "Die trimetrische Projektion von W. Chamberlin". 39. Kartographische Nachrichten. pp. 51–55. 

External links

• The Chamberlin Trimetric Projection - Implementations of the projection using Matlab scripts.
• The Chamberlin Trimetric Projection - Notes on the projection from a cartography class at Colorado State University.
• National Geographic Map Collection - Many examples of National Geographic Society maps employing the Chamberlin Trimetric Projection can be seen here.