Singular function

The graph of the winding number of the circle map is an example of a singular function.

In mathematics, a singular function is any function ƒ defined on the interval [a, b] that has the following properties:

• ƒ is continuous on [a, b]. (**)
• there exists a set N of measure 0 such that for all x outside of N the derivative ƒ ′(x) exists and is zero, that is, the derivative of f vanishes almost everywhere.
• ƒ is nondecreasing on [a, b].
• ƒ(a) < ƒ(b).

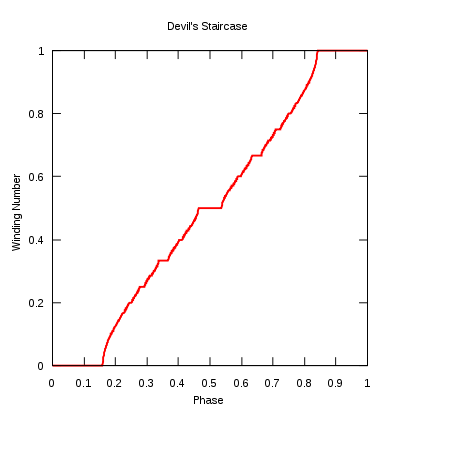
A standard example of a singular function is the Cantor function, which is sometimes called the devil's staircase (a term also used for singular functions in general). There are, however, other functions that have been given that name. One is defined in terms of the circle map.

If ƒ(x) = 0 for all x ≤ a and ƒ(x) = 1 for all x ≥ b, then the function can be taken to represent a cumulative distribution function for a random variable which is neither a discrete random variable (since the probability is zero for each point) nor an absolutely continuous random variable (since the probability density is zero everywhere it exists).

Singular functions occur, for instance, as sequences of spatially modulated phases or structures in solids and magnets, described in a prototypical fashion by the model of Frenkel and Kontorova and by the ANNNI model, as well as in some dynamical systems. Most famously, perhaps, they lie at the center of the fractional quantum Hall effect.

See also

• Absolute continuity

References

(**) This condition depends on the references ^[1]

1. ^ singular function -- Springer Online Reference Works, http://eom.springer.de/s/s085550.htm 

• Lebesgue, H. (1955-1961), Theory of functions of a real variable, F. Ungar 

• Halmos, P.R. (1950), Measure theory, v. Nostrand 

• Royden, H.L (1988), Real Analysis, Prentice-Hall, Englewood Cliffs, New Jersey 

• Lebesgue, H. (1928), Leçons sur l'intégration et la récherche des fonctions primitives, Gauthier-Villars