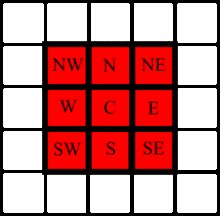
Moore neighborhood

The Moore neighborhood comprises eight cells which surround center C.

In cellular automata, the Moore neighborhood comprises the eight cells surrounding a central cell on a two-dimensional square lattice. The neighborhood is named after Edward F. Moore, a pioneer of cellular automata theory. It is one of the two most commonly used neighborhood types, the other one being the 4-cell von Neumann neighborhood. The well known Conway's Game of Life, for example, uses the Moore neighborhood. It is similar to the notion of 8-connected pixels in computer graphics.

The concept can be extended to higher dimensions, for example forming a 26-cell cubic neighborhood for a cellular automaton in three dimensions.

The Moore neighbourhood of a point is the points at a Chebyshev distance of 1.

Algorithm

The idea behind the formulation of Moore neighborhood is to find the contour of a given graph. This idea was a great challenge for most analysts of the 18th century, and as a result an algorithm was derived from the Moore graph which was later then called the Moore Neighborhood algorithm.

The following is a formal description of the Moore-Neighbor tracing algorithm: Input: A square tessellation, T, containing a connected component P of black cells. Output: A sequence B (b1, b2 ,..., bk) of boundary pixels i.e. the contour. Define M(a) to be the Moore neighborhood of pixel a. Let p denote the current boundary pixel. Let c denote the current pixel under consideration i.e. c is in M(p). Let b denote the backtrack of c (i.e. neighbor pixel of p that was previously tested)

  Begin
  Set B to be empty.
  From bottom to top and left to right scan the cells of T until a black pixel, s, of P is found.
  Insert s in B.
  Set the current boundary point p to s i.e. p=s
  b = the pixel from which s was entered during the image scan.
  Set c to be the next clockwise pixel (from b) in M(p).
  While c not equal to s do
    If c is black
      insert c in B
      b = p
      p = c
      (backtrack: move the current pixel c to the pixel from which p was entered)
      c = next clockwise pixel (from b) in M(p).
    else
      (advance the current pixel c to the next clockwise pixel in M(p) and update backtrack)
      b = c
      c = next clockwise pixel (from b) in M(p).
    end While
  End

Termination Condition

The original termination condition was to stop after visiting the start pixel for the second time. This limits the set of contours the algorithm will walk completely. An improved stopping condition proposed by Jacob Eliosoff is to stop after entering the start pixel for the second time in the same direction you originally entered it.

Applications

Because of its flexibility, it is widely used on most image editing software such as the Photoshop line of Adobe Systems and the MX Fireworks of Macromedia. It is used on their image editing tool with concerns regarding cellular automata on image engine. Some of these tools are the edge finder and magic wand which greatly deals with the proper management and allocation of the boundary and edge of a digital image

See also

• Neighbourhood (graph theory)
• King's graph

References

• Weisstein, Eric W., "Moore Neighborhood" from MathWorld.
• Tyler, Tim, The Moore neighborhood at cell-auto.com