Trigonometric integral

Si(x) (blue) and Ci(x) (green) plotted on the same plot.

In mathematics, the trigonometric integrals are a family of integrals which involve trigonometric functions. A number of the basic trigonometric integrals are discussed at the list of integrals of trigonometric functions.

Sine integral

Plot of Si(x) for 0 ≤ x ≤ 8π.

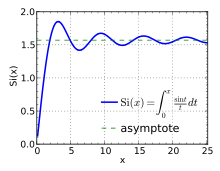
The different sine integral definitions are:

${\rm Si}(x) = \int_0^x\frac{\sin t}{t}\,dt$

${\rm si}(x) = -\int_x^\infty\frac{\sin t}{t}\,dt$

Si(x) is the primitive of sinx / x which is zero for x = 0; si(x) is the primitive of sinx / x which is zero for $x=\infty$.

Note that $\frac{\sin t}{t}$ is the sinc function and also the zeroth spherical Bessel function.

When $x=\infty$, this is known as the Dirichlet integral.

In signal processing, the oscillations of the Sine integral cause overshoot and ringing artifacts when using the sinc filter, and frequency domain ringing if using a truncated sinc filter as a low-pass filter.

The Gibbs phenomenon is a related phenomenon: thinking of sinc as a low-pass filter, it corresponds to truncating the Fourier series, which causes the Gibbs phenomenon.

Cosine integral

Plot of Ci(x) for 0 < x ≤ 8π.

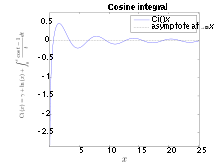
The different cosine integral definitions are:

${\rm Ci}(x) = \gamma + \ln x + \int_0^x\frac{\cos t-1}{t}\,dt$

${\rm ci}(x) = -\int_x^\infty\frac{\cos t}{t}\,dt$

${\rm Cin}(x) = \int_0^x\frac{1-\cos t}{t}\,dt$

ci(x) is the primitive of cos x / x which is zero for $x=\infty$. We have:

${\rm ci}(x)={\rm Ci}(x)\,$

${\rm Cin}(x)=\gamma+\ln x-{\rm Ci}(x)\,$

Hyperbolic sine integral

The hyperbolic sine integral:

${\rm Shi}(x) = \int_0^x\frac{\sinh t}{t}\,dt = {\rm shi}(x).$

Hyperbolic cosine integral

The hyperbolic cosine integral:

${\rm Chi}(x) = \gamma+\ln x + \int_0^x\frac{\cosh t-1}{t}\,dt = {\rm chi}(x)$

where γ is the Euler–Mascheroni constant.

Nielsen's spiral

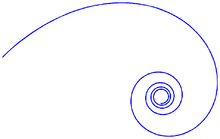
Nielsen's spiral.

The spiral formed by parametric plot of si,ci is known as Nielsen's spiral. It is also referred to as the Euler spiral, the Cornu spiral, a clothoid, or as a linear-curvature polynomial spiral. The spiral is also closely related to the Fresnel integrals. This spiral has applications in vision processing, road and track construction and other areas.

Expansion

Various expansions can be used for evaluation of Trigonometric integrals, depending on the range of the argument.

Asymptotic series (for large argument)

${\rm Si}(x)=\frac{\pi}{2} - \frac{\cos x}{x}\left(1-\frac{2!}{x^2}+\cdots\right) - \frac{\sin x}{x}\left(\frac{1}{x}-\frac{3!}{x^3}+\cdots\right)$

${\rm Ci}(x)= \frac{\sin x}{x}\left(1-\frac{2!}{x^2}+\cdots\right) -\frac{\cos x}{x}\left(\frac{1}{x}-\frac{3!}{x^{3}}+\cdots\right)$

These series are divergent^{[clarification needed]}, although can be used for estimates and even precise evaluation at $~{\rm Re} (x) \gg 1~$.

Convergent series

${\rm Si}(x)= \sum_{n=0}^\infty \frac{(-1)^{n}x^{2n+1}}{(2n+1)(2n+1)!}=x-\frac{x^3}{3!\cdot3}+\frac{x^5}{5!\cdot5}-\frac{x^7}{7! \cdot7}\pm\cdots$

${\rm Ci}(x)= \gamma+\ln x+\sum_{n=1}^{\infty}\frac{(-1)^{n}x^{2n}}{2n(2n)!}=\gamma+\ln x-\frac{x^2}{2!\cdot2}+\frac{x^4}{4! \cdot4}\mp\cdots$

These series are convergent at any complex $~x~$, although for $|x|\gg 1$ the series will converge slowly initially, requiring many terms for high precision.

Relation with the exponential integral of imaginary argument

Function ${\rm E}_1(z) = \int_1^\infty \frac {\exp(-zt)} {t} {\rm d} t \qquad({\rm Re}(z) \ge 0)$ is called exponential integral. It is closely related with Si and Ci:

${\rm E}_1( {\rm i}\!~ x)= i\left(-\frac{\pi}{2} +{\rm Si}(x)\right)-{\rm Ci}(x) = i~{\rm si}(x) - {\rm ci}(x) \qquad(x>0)$

As each involved function is analytic except the cut at negative values of the argument, the area of validity of the relation should be extended to Re(x) > 0. (Out of this range, additional terms which are integer factors of π appear in the expression).

Cases of imaginary argument of the generalized integro-exponential function are $\int_1^\infty \cos(ax)\frac{\ln x}{x}dx = -\frac{\pi^2}{24}+\gamma(\frac{\gamma}{2}+\ln a)+\frac{\ln^2a}{2} +\sum_{n\ge 1}\frac{(-a^2)^n}{(2n)!(2n)^2},$

which is the real part of

$\int_1^\infty e^{iax}\frac{\ln x}{x}dx = -\frac{\pi^2}{24} +\gamma(\frac{\gamma}{2}+\ln a)+\frac{\ln^2 a}{2}-\frac{\pi}{2}i(\gamma+\ln a) +\sum_{n\ge 1}\frac{(ia)^n}{n!n^2}.$

Similarly $\int_1^{\infty} e^{iax}\frac{\ln x}{x^2}dx =1+ia[-\frac{\pi^2}{24}+\gamma(\frac{\gamma}{2}+\ln a-1)+\frac{\ln^2 a}{2}-\ln a+1 -\frac{i\pi}{2}(\gamma+\ln a-1)]+\sum_{n\ge 1}\frac{(ia)^{n+1}}{(n+1)!n^2}.$

See also

• Exponential integral
• Logarithmic integral

Signal processing

• Gibbs phenomenon
• Ringing artifacts

References

• Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 5", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, pp. 231, ISBN 978-0486612720, MR0167642, http://www.math.sfu.ca/~cbm/aands/page_231.htm .
• Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Section 6.8.2. Cosine and Sine Integrals", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8, http://apps.nrbook.com/empanel/index.html#pg=300 
• Temme, N. M. (2010), "Exponential, Logarithmic, Sine, and Cosine Integrals", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR2723248, http://dlmf.nist.gov/6 
• A bot will complete this citation soon. Click here to jump the queuearXiv:0912.3844. , Appendix B.