Fresnel integral

S(x) and C(x) The maximum of C(x) is about 0.977451424. If πt²/2 were used instead of t², then the image would be scaled vertically and horizontally (see below).

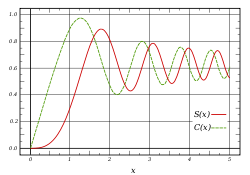
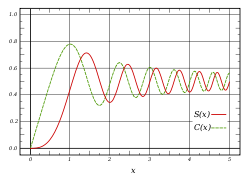
Fresnel integrals, S(x) and C(x), are two transcendental functions named after Augustin-Jean Fresnel that are used in optics. They arise in the description of near field Fresnel diffraction phenomena, and are defined through the following integral representations:

$S(x)=\int_0^x \sin(t^2)\,dt,\quad C(x)=\int_0^x \cos(t^2)\,dt.$

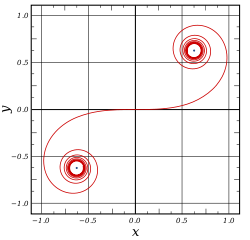
The simultaneous parametric plot of S(x) and C(x) is the Euler spiral, also known as the Cornu spiral or clothoid.

Definition

The Fresnel integrals admit the following power series expansions that converge for all x:

Normalised Fresnel integrals, S(x) and C(x). In these curves, the argument of the trigonometric function is πt²/2, as opposed to just t² as above.

$S(x)=\int_0^x \sin(t^2)\,dt=\sum_{n=0}^{\infin}(-1)^n\frac{x^{4n+3}}{(2n+1)!(4n+3)},$

$C(x)=\int_0^x \cos(t^2)\,dt=\sum_{n=0}^{\infin}(-1)^n\frac{x^{4n+1}}{(2n)!(4n+1)}.$

Some authors, including Abramowitz and Stegun, (eqs 7.3.1 – 7.3.2) use $\frac{\pi}{2}t^2$ for the argument of the integrals defining S(x) and C(x). To get these functions, multiply the above integrals by $\sqrt{\frac{2}{\pi}}$ and divide the argument x by the same factor.

Euler spiral

Main article: Euler spiral

Euler spiral (x, y) = (C(t), S(t)). The spiral converges to the centre of the holes in the image as t tends to positive or negative infinity.

The Euler spiral, also known as Cornu spiral or clothoid, is the curve generated by a parametric plot of S(t) against C(t). The Cornu spiral was created by Marie Alfred Cornu as a nomogram for diffraction computations in science and engineering.

From the definitions of Fresnel integrals, the infinitesimals dx and dy are thus:

$dx = C'(t)dt = \cos(t^2) dt \,$

$dy = S'(t)dt = \sin(t^2) dt \,$

Thus the length of the spiral measured from the origin can be expressed as:

$L = \int_0^t {\sqrt {dx^2 + dy^2}} = \int_0^t{dt} = t$

That is, the parameter t is the curve length measured from the origin (0,0) and the Euler spiral has infinite length. The vector [cos(t²), sin(t²)] also expresses the unit tangent vector along the spiral, giving θ = t². Since t is the curve length, the curvature, κ can be expressed as:

$\kappa = \tfrac {1}{R} = \tfrac {d\theta}{dt} = 2t$

And the rate of change of curvature with respect to the curve length is:

$\tfrac {d^2\theta}{dt^2} = 2$

An Euler spiral has the property that its curvature at any point is proportional to the distance along the spiral, measured from the origin. This property makes it useful as a transition curve in highway and railway engineering.

If a vehicle follows the spiral at unit speed, the parameter t in the above derivatives also represents the time. That is, a vehicle following the spiral at constant speed will have a constant rate of angular acceleration.

Sections from Euler spirals are commonly incorporated into the shape of roller-coaster loops to make what are known as "clothoid loops".

Properties

• C(x) and S(x) are odd functions of x.
• C and S are entire functions.
• Using the power series expansions above, the Fresnel integrals can be extended to the domain of complex numbers, and they become analytic functions of a complex variable. The Fresnel integrals can be expressed using the error function as follows:

$S(x)=\frac{\sqrt{\pi}}{4} \left( \sqrt{i}\,\operatorname{erf}(\sqrt{i}\,x) + \sqrt{-i}\,\operatorname{erf}(\sqrt{-i}\,x) \right)$

$C(x)=\frac{\sqrt{\pi}}{4} \left( \sqrt{-i}\,\operatorname{erf}(\sqrt{i}\,x) + \sqrt{i}\,\operatorname{erf}(\sqrt{-i}\,x) \right).$

• The integrals defining C(x) and S(x) cannot be evaluated in the closed form in terms of elementary functions, except in special cases. The limits of these functions as x goes to infinity are known:

$\int_{0}^{\infty} \cos t^2\,dt = \int_{0}^{\infty} \sin t^2\,dt = \frac{\sqrt{2\pi}}{4} = \sqrt{\frac{\pi}{8}}.$

Evaluation

The sector contour used to calculate the limits of the Fresnel integrals

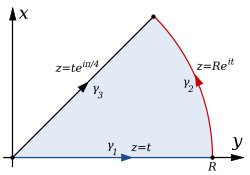
The limits of C and S as the argument tends to infinity can be found by the methods of complex analysis. This uses the contour integral of the function

$e^{-\frac{1}{2}t^2}$

around the boundary of the sector-shaped region in the complex plane formed by the positive x-axis, the half-line y = x, x ≥ 0, and the circle of radius R centered at the origin.

As R goes to infinity, the integral along the circular arc tends to 0, the integral along the real axis tends to the Gaussian integral

$\int_{0}^{\infty} e^{-\frac{1}{2}t^2}dt = \sqrt{\frac {\pi}{2}},$

and after routine transformations, the integral along the bisector of the first quadrant can be related to the limit of the Fresnel integrals.

Generalization

The Fresnel integral can be generalized by the function

$\int_0^\infty\sin(x^a)\ dx = \frac{\Gamma\left(\frac{1}{a}\right)\sin(\frac{\pi}{2a})}{a}$

with the left-hand side converging for a>1 and the right-hand side being its analytical extension to the whole plane less where lie the poles of Γ(a ^{− 1}).

See also

• Augustin-Jean Fresnel
• Fresnel zone
• Track transition curve
• Euler spiral
• Zone plate

References

• R. Nave, The Cornu spiral, Hyperphysics (2002) (Uses πt²/2 instead of t².)
• Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 7", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, pp. 297, ISBN 978-0486612720, MR0167642, http://www.math.sfu.ca/~cbm/aands/page_297.htm .
• Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Section 6.8.1. Fresnel Integrals", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8, http://apps.nrbook.com/empanel/index.html#pg=297 
• Temme, N. M. (2010), "Error Functions, Dawson’s and Fresnel Integrals", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR2723248, http://dlmf.nist.gov/7 

External links

• Weisstein, Eric W., "Fresnel Integrals" from MathWorld.
• Weisstein, Eric W., "Cornu Spiral" from MathWorld.
• "Roller Coaster Loop Shapes". http://fy.chalmers.se/LISEBERG/eng/loop_pe.html. Retrieved 2008-08-13. ^{[dead link]}