Drainage equation

A drainage equation is an equation describing the relation between depth and spacing of parallel subsurface drains, depth of the watertable, depth and hydraulic conductivity of the soils. It is used in drainage design.

Parameters in Hooghoudt's drainage equation

A well known steady-state drainage equation is the Hooghoudt drain spacing equation. Its original publication is in Dutch.^[1] The equation was introduced in the USA by van Schilfgaarde.^[2]

Hooghoudt's equation

Hooghoudt's equation can be written as:.^[3]

Q L² = 8 Kb d (Di - Dd) (Dd - Dw) + 4 Ka (Dd - Dw)²

where:

• Q = steady state drainage discharge rate (m/day)
• Ka = hydraulic conductivity of the soil above drain level (m/day)
• Kb = hydraulic conductivity of the soil below drain level (m/day)
• Di = depth of the impermeable layer below drain level (m)
• Dd = depth of the drains (m)
• Dw = steady state depth of the watertable midway between the drains (m)
• L = spacing between the drains (m)
• d = equivalent depth, a function of L, (Di-Dd), and r
• r = drain radius (m)

Steady (equilibrium) state condition
In steady state, the level of the water table remains constant and the discharge rate (Q) equals the rate of groundwater recharge (R), i.e. the amount of water entering the groundwater through the watertable per unit of time. By considering a long-term (e.g. seasonal) average depth of the water table (Dw) in combination with the long-term average recharge rate (R), the net storage of water in that period of time is negligibly small and the steady state condition is satisfied: one obtains a dynamic equilibrium.

Derivation of the equation
For the derivation of the equation Hooghoudt used the law of Darcy, the summation of circular potential functions and, for the determination of the influence of the impermeable layer, de method of mirror images and superposition.
Hooghoudt published tables for the determination of the equivalent depth (d), because the function (F) in d = F (L,Di-Dd,r) consists of long series of terms.

Crop yield and seasonal average depth of the water table

Determining:

• the discharge rate (Q) from the recharge rate (R) in a water balance as detailed in the article: hydrology (agriculture)
• the permissible long term average depth of the water table (Dw) on the basis of agricultural drainage criteria
• the soil's hydraulic conductivity (Ka and Kb) by measurements
• the depth of the bottom of the aquifer (Di)

the design drain spacing (L) can be found from the equation in dependence of the drain depth (Dd) and drain radius (r).

Drainage criteria
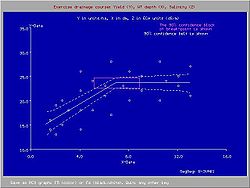
One would not want the water table to be too shallow to avoid crop yield depression nor too deep to avoid drought conditions. This is a subject of drainage research. The figure shows that a seasonal average depth of the water table shallower than 70 cm causes a yield depression ^[4]
The figure was made with the SegReg program for segmented regression.^[5]

Equivalent depth

In 1991 a closed-form expression was developed for the equivalent depth (d) that can replace the Hooghoudt tables ^[6] :

d = πL / 8 { ln(L/πr) + F(x) }

where:

• x = 2π (Di − Dd) / L
• F(x) = Σ 4e^−2nx / n (1 − e^−2nx) , with n = 1, 3, 5, . . .

Extended use

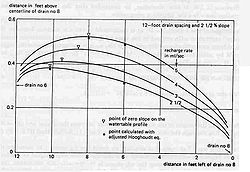
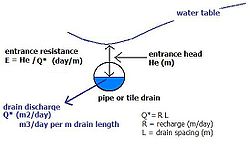
Theoretically, Hooghoudt's equation can also be used for sloping land.^[7] The theory on drainage of sloping land is corroborated by the results of sand tank experiments.^[8] In addition, the entrance resistance encountered by the water upon entering the drains can be accounted for.

• Definitions of drainage of sloping land and entrance resistance
• 

  Geometry of drains in sloping land used in the theory

• 

  Corroboration with drainage experiments in a sloping sand tank

• 

  Definition of entrance resistance

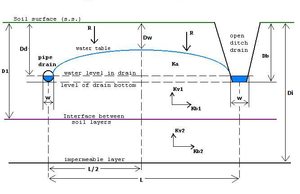
Amplification

Amplification of parameters compared to Hooghoudt

The drainage formula can be amplified ^[9] to account for (see figure on the right):

• the additional energy associated with the incoming percolation water (recharge), see groundwater energy balance
• multiple soil layers
• anisotropric hydraulic conductivity, the vertical conductivity (Kv) being different from the horizontal (Kh)
• drains of different dimensions with any width (W)

EnDrain: shape of the watertable with drainage

Computer program

The amplified drainage equation uses an hydraulic equivalent of Joule's law in electricity.

It is in the form of a differential equation that cannot be solved analytically (i.e. in a closed form) but the solution requires a numerical method for which a computer program is indispensable.

The availability of a computer program also helps in quickly assessing various alternatives and performing a sensitivity analysis.

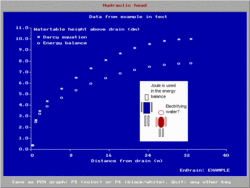
The blue figure shows an example of results of a computer aided calculation with the amplified drainage equation using the EnDrain program.^[10] It shows that incorporation of the incoming energy associated with the recharge leads to a somewhat deeper water table.

See also

External links

• Website with free download of articles and software on land drainage: [10]
• A chapter on agricultural drainage criteria: [11]
• A chapter on determining hydraulic conductivity: [12]

References

1. ^ S.B.Hooghoudt, 1940 (in Dutch). Algemene beschouwing van het probleem van de detailontwatering en de infiltratie door middel van parallel loopende drains, greppels, slooten en kanalen. No. 7 in de serie: Bijdragen tot de kennis van eenige natuurkundige grootheden van den grond. Bodemkundig Instituut te Groningen. Rijksuitgeverij Dienst van de Nderlandse Staatscourant. 's-Gravenhage, Algemeene Landsdrukkerij.
2. ^ J. van Schilfgaarde, 1957. Approximate solutions to drainage flow problems. In: J.N.Luthin (Ed.), Drainage of agricultural lands, p.79-112. Agron. Monogr. 7. ASA, Madison, WI, USA.
3. ^ H.P.Ritzema, 1994, Subsurface flow to drains. Chapter 8 in: H.P.Ritzema (ed.), Drainage Principles and Applications, Publ. 16, pp. 236-304, International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. ISBN 90 70754 3 39
4. ^ Drainage research in farmers' fields: analysis of data. Contribution to the project “Liquid Gold” of the International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. Download from web page : [1] , under nr. 2, or directly as PDF : [2]
5. ^ The computer program SegReg for segmented regression can be downloaded freely from web page : [3] , or from : [4]
6. ^ W.H. van der Molen en J.Wesseling, 1991. A solution in closed form and a series solution to replace the tables for the thickness of the equivalent layer in Hooghoudt's drain spacing equation. Agricultural Water Management 19, pp.1-16
7. ^ Hooghoudt's drainage equation adjusted for entrance resistance and sloping land. International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. On line : [5] . Updated version of: R.J. Oosterbaan, “Interception drainage and drainage of sloping lands” published in: Bulletin of the Irrigation, Drainage and Flood Control Council, Pakistan, Vol. 5, No. 1, June 1975.
8. ^ Zeigler, E.R. 1972. Laboratory tests to study drainage from sloping land. Report REC ERC 72 4, Engineering and Research Center, Bureau of Reclamation, Denver, Col., U.S.A.
9. ^ The energy balance of groundwater flow applied to subsurface drainage in anisotropic soils by pipes or ditches with entrance resistance. International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. On line : [6] . Paper based on: R.J. Oosterbaan, J. Boonstra and K.V.G.K. Rao, 1996, “The energy balance of groundwater flow”. Published in V.P.Singh and B.Kumar (eds.), Subsurface-Water Hydrology, p. 153-160, Vol.2 of Proceedings of the International Conference on Hydrology and Water Resources, New Delhi, India, 1993. Kluwer Academic Publishers, Dordrecht, The Netherlands. ISBN 978-0-7923-3651-8 . On line : [7]
10. ^ The free computer program EnDrain can be downloaded from web page : [8] , or from : [9]