Transformation (function)

In mathematics, a transformation could be any function mapping a set X on to another set or on to itself. However, often the set X has some additional algebraic or geometric structure and the term "transformation" refers to a function from X to itself that preserves this structure.

Examples include linear transformations and affine transformations, rotations, reflections and translations. These can be carried out in Euclidean space, particularly in dimensions 2 and 3. They are also operations that can be performed using linear algebra, and described explicitly using matrices.

Translation

Main article: Translation (geometry)

A translation, or translation operator, is an affine transformation of Euclidean space which moves every point by a fixed distance in the same direction. It can also be interpreted as the addition of a constant vector to every point, or as shifting the origin of the coordinate system. In other words, if v is a fixed vector, then the translation T_v will work as T_v(p) = p + v.

Let us have a clear visualization of this. In day to day life we use computers in all fields. Let us consider this window. This window if maximized to full dimensions of the screen is the reference plane. Imagine one of the corners as the reference point or origin (0, 0).

Consider a point P(x, y)in the corresponding plane. Now the axes are shifted from the original axes to a distance (h, k) and this is the corresponding reference axes. Now the origin (previous axes) is (x, y) and the point P is (X, Y) and therefore the equations are:

X = x − h or x = X + h or h = x − X and Y = y − k or y = Y + k or k = y − Y.

Replacing these values or using these equations in the respective equation we obtain the transformed equation or new reference axes, old reference axes, point lying on the plane.

Reflection

Main article: Reflection (mathematics)

A reflection is a map that transforms an object into its mirror image with respect to a "mirror", which is a hyperplane of fixed points in the geometry. For example, a reflection of the small English letter p in respect to a vertical line would look like q. In order to reflect a planar figure one needs the "mirror" to be a line (axis of reflection or axis of symmetry), while for reflections in the three-dimensional space one would use a plane (the plane of reflection or symmetry) for a mirror. Reflection may be considered as the limiting case of inversion as the radius of the reference circle increases without bound.

Reflection is considered to be an opposite motion since it changes the orientation of the figures it reflects.

Glide reflection

Main article: Glide reflection

Example of a glide reflection

A glide reflection is a type of isometry of the Euclidean plane: the combination of a reflection in a line and a translation along that line. Reversing the order of combining gives the same result. Depending on context, we may consider a reflection a special case, where the translation vector is the zero vector.

Rotation

Main article: Rotation (geometry)

A rotation is a transformation that is performed by "spinning" the object around a fixed point known as the center of rotation. You can rotate your object at any degree measure, but 90° and 180° are two of the most common. Also, rotations are done counterclockwise (Anticlockwise).

Scaling

Main article: Scaling (geometry)

Uniform scaling is a linear transformation that enlarges or diminishes objects; the scale factor is the same in all directions; it is also called a homothety. The result of uniform scaling is similar (in the geometric sense) to the original.

More general is scaling with a separate scale factor for each axis direction; a special case is directional scaling (in one direction). Shapes not aligned with the axes may be subject to shear (see below) as a side effect: although the angles between lines parallel to the axes are preserved, other angles are not.

Shear

Main article: Shear mapping

Shear is a transform that effectively rotates one axis so that the axes are no longer perpendicular. Under shear, a rectangle becomes a parallelogram, and a circle becomes an ellipse. Even if lines parallel to the axes stay the same length, others do not. As a mapping of the plane, it lies in the class of equi-areal mappings.

More generally

Main article: Linear transformation

More generally, a transformation in mathematics means a mathematical function (synonyms: map and mapping). A transformation can be an invertible function from a set X to itself, or from X to another set Y. The choice of the term transformation may simply flag that a function's more geometric aspects are being considered (for example, with attention paid to invariants).

A strong non-linear transformation applied to a plane through the origin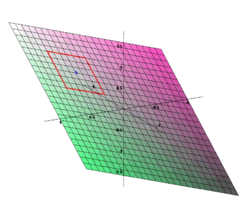

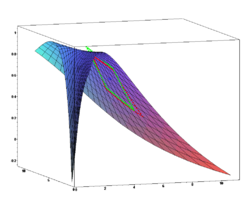
Before	After

See also

• Coordinate transformation
• Data transformation (statistics)
• Infinitesimal transformation
• Linear transformation
• Transformation geometry
• Transformation group
• Transformation matrix