Molecular diffusion

This article is about spontaneous dispersion of mass. For a more generic treatment of diffusion, see Diffusion.

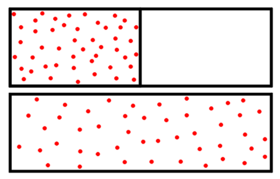
Diffusion from a microscopic and macroscopic point of view. Initially, there are solute molecules on the left side of a barrier (purple line) and none on the right. The barrier is removed, and the solute diffuses to fill the whole container. Top: A single molecule moves around randomly. Middle: With more molecules, there is a clear trend where the solute fills the container more and more uniformly. Bottom: With an enormous number of solute molecules, all randomness is gone: The solute appears to move smoothly and systematically from high-concentration areas to low-concentration areas, following Fick's laws.

Molecular diffusion, often called simply diffusion, is the thermal motion of all (liquid or gas) particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size (mass) of the particles. Diffusion explains the net flux of molecules from a region of higher concentration to one of lower concentration, but it is important to note that diffusion also occurs when there is no concentration gradient. The result of diffusion is a gradual mixing of material. In a phase with uniform temperature, absent external net forces acting on the particles, the diffusion process will eventually result in complete mixing.

Diffusive equilibrium is reached when the concentrations of the diffusing substance in the two compartments becomes equal.

Consider two systems; S₁ and S₂ at the same temperature and capable of exchanging particles. If there is a change in the potential energy of a system; for example μ₁>μ₂ (μ is Chemical potential) an energy flow will occur from S₁ to S₂, because nature always prefers low energy and maximum entropy.

Though the different systems are at equilibrium, there is still water passing through the semipermeable membrane. So if food coloring is put in system A, eventually it would be of equal color to system B.

Molecular diffusion is typically described mathematically using Fick's laws of diffusion.

Applications

Diffusion is of fundamental importance in many disciplines of physics, chemistry, and biology. Some example applications of diffusion:

• Sintering to produce solid materials (powder metallurgy, production of ceramics)
• Chemical reactor design
• Catalyst design in chemical industry
• Steel can be diffused (e.g., with carbon or nitrogen) to modify its properties
• Doping during production of semiconductors.

Significance

Schematic representation of mixing of two substances by diffusion

Diffusion is part of the transport phenomena. Of mass transport mechanisms, molecular diffusion is known as a slower one.

Biology

In cell biology, diffusion is a main form of transport for necessary materials such as amino acids within cells.^[1] Diffusion of water (H₂O) through a partially permeable membrane is classified as osmosis.

Metabolism and respiration rely in part upon diffusion in addition to bulk or active processes. For example, in the alveoli of mammalian lungs, due to differences in partial pressures across the alveolar-capillary membrane, oxygen diffuses into the blood and carbon dioxide diffuses out. Lungs contain a large surface area to facilitate this gas exchange process.

Tracer and chemical diffusion

Self diffusion, exemplified with an isotopic tracer of radioactive isotope ²²Na

Example of chemical (classical, Fick's, or Fickian) diffusion of sodium chloride in water

Fundamentally, two types of diffusion are distinguished:

• Tracer diffusion, which is a spontaneous mixing of molecules taking place in the absence of concentration (or chemical potential) gradient. This type of diffusion can be followed using isotopic tracers, hence the name. The tracer diffusion is usually assumed to be identical to self-diffusion (assuming no significant isotopic effect). This diffusion can take place under equilibrium.
• Chemical diffusion occurs in a presence of concentration (or chemical potential) gradient and it results in net transport of mass. This is the process described by the diffusion equation. This diffusion is always a non-equilibrium process, increases the system entropy, and brings the system closer to equilibrium.

The diffusion coefficients for these two types of diffusion are generally different because the diffusion coefficient for chemical diffusion is binary and it includes the effects due to the correlation of the movement of the different diffusing species.

Non-equilibrium system

Illustration of low entropy (top) and high entropy (bottom)

Because chemical diffusion is a net transport process, the system in which it takes place is not an equilibrium system (i.e. it is not at rest yet). Many results in classical thermodynamics are not easily applied to non-equilibrium systems. However, there sometimes occur so-called quasi-steady states, where the diffusion process does not change in time, where classical results may locally apply. As the name suggests, this process is a not a true equilibrium since the system is still evolving.

Non-equilibrium fluid systems can be successfully modeled with Landau-Lifshitz fluctuating hydrodynamics. In this theoretical framework, diffusion is due to fluctuations whose dimensions range from the molecular scale to the macroscopic scale.^[2]

Chemical diffusion increases the entropy of a system, i.e. diffusion is a spontaneous and irreversible process. Particles can spread out by diffusion, but will not spontaneously re-order themselves (absent changes to the system, assuming no creation of new chemical bonds, and absent external forces acting on the particle).

Concentration dependent "collective" diffusion

Collective diffusion is the diffusion of a large number of particles, most often within a solvent.

Contrary to brownian motion, which is the diffusion of a single particle, interactions between particles may have to be considered, unless the particles form an ideal mix with their solvent (ideal mix conditions correspond to the case where the interactions between the solvent and particles are identical to the interactions between particles and the interactions between solvent molecules; in this case, the particles do not interact when inside the solvent).

In case of an ideal mix, the particle diffusion equation holds true and the diffusion coefficient D the speed of diffusion in the particle diffusion equation is independent of particle concentration. In other cases, resulting interactions between particles within the solvent will account for the following effects:

• the diffusion coefficient D in the particle diffusion equation becomes dependent of concentration. For an attractive interaction between particles, the diffusion coefficient tends to decrease as concentration increases. For a repulsive interaction between particles, the diffusion coefficient tends to increase as concentration increases.
• In the case of an attractive interaction between particles, particles exhibit a tendency to coalesce and form clusters if their concentration lies above a certain threshold. This is equivalent to a precipitation chemical reaction (and if the considered diffusing particles are chemical molecules in solution, then it is a precipitation).

Molecular Diffusion of Gases

Transport of material in stagnant fluid or across streamlines of a fluid in a laminar flow occurs by molecular diffusion.Two adjacent compartments, separated by partition containing pure gases A or B may be envisaged. Random movement of all molecules occurs so that after a period molecules are found remote from their original positions. If the partition is removed, some molecules of A move towards the region occupied by B, their number depends on the number of molecules at the point considered. Concurrently, molecules of B diffuse toward regimens formerly occupied by pure A. Finally, complete mixing occurs. Before this point in time, a gradual variation in the concentration of A occurs along an axis, designated x, which joins the original compartments. This variation, expressed mathematically -dC_A/dx, where CA is the concentration of A. The negative sign arises because the concentration of A decreases as the distance x increases. Similarly, the variation in the concentration of gas B is -dC_B/dx. The rate of diffusion of A, N_A, depend on concentration gradient and the average velocity with which the molecules of A moves in the x direction. This relationship is expressed by Fick's Law

$N_{A}= -D_{AB} \frac{dC_{A}}{dx}$ "only applicable for no bulk motion"

where D is the Diffusivity of A through B, proportional to the average molecular velocity and, therefore depend on the temperature and pressure of gases. The rate of Diffusion N_A,is usually expressed as the number of moles diffusing across unit area in unit time. As with the basic equation of heat transfer, indicates that the rate of force is directly proportional to the driving force, which is the concentration gradient.

This basic equation applied to a number of situations. Restricting discussion exclusively to steady state conditions, in which neither dC_A/dx or dC_B/dx change with time, equimolecular counterdiffusion is considered first.

Equimolecular Counterdiffusion

If no bulk flow occurs in an element of length dx, the rates of diffusion of two gases A and B must be equal and opposite, that is N_A=-N_B.

The partial pressure of A changes by dP_A over the distance dx. Similarly, the partial pressure of B changes dP_B. As there is no difference in total pressure across the element (no bulk flow), dP_A/dx must equal -dP_B/dx. For an ideal gas the partial pressure is related to the molar concentration by the relation

P_AV = n_ART

where n_A is the number of moles of gas A in a volume V. As the molar concentration C_A is equal to n_A/ V therefore

P_A = C_ART

Consequently, for gas A,

$N_{A}=-D_{AB} \frac{dP_{A}}{RT} dx$

where D_AB is the diffusivity of A in B. Similarly,

$N_{B}=-D_{BA} \frac{dP_{B}}{RT}dx=D_{AB} \frac{dP_{A}}{RT}dx$

It therefore allows that D_AB=D_BA=D. If the partial pressure of A at x₁ is P_A1 and x₂ is P_A2, integration of above equation,

$N_{A}=-\frac{D}{RT} \frac{(P_{A2}-P_{A1})}{x_{2}-x_{1}}$

A similar equation may be derived for the counterdiffusion of gas B.

See also

• Molecular diffusion of gases
• Equimolecular counterdiffusion
• Ambipolar diffusion
• Anomalous diffusion
• Batchelor scale
• Bohm diffusion
• Diffusion MRI
• Double diffusive convection
• Drag (physics)
• Fick's laws of diffusion
• Local time (mathematics)
• Mass transfer
• Mass flux
• Osmosis
• Permeation
• Relativistic heat conduction
• Transport phenomena
• Turbulent diffusion
• Viscosity

References

1. ^ Maton, Anthea; Jean Hopkins, Susan Johnson, David LaHart, Maryanna Quon Warner, Jill D. Wright (1997). Cells Building Blocks of Life. Upper Saddle River, New Jersey: Prentice Hall. pp. 66–67. 
2. ^ D. Brogioli and A. Vailati, Diffusive mass transfer by nonequilibrium fluctuations: Fick's law revisited, Phys. Rev. E 63, 012105/1-4 (2001)

External links

• Some pictures that display diffusion and osmosis
• An animation describing diffusion.
• A tutorial on the theory behind and solution of the Diffusion Equation.
• NetLogo Simulation Model for Educational Use (Java Applet)
• Short movie on brownian motion (includes calculation of the diffusion coefficient)
• A basic introduction to the classical theory of volume diffusion (with figures and animations)
• Diffusion on the nanoscale (with figures and animations)

Internal links

• Doping (semiconductor) – A reference on doping semiconductors