Church–Kleene ordinal

In mathematics, the Church–Kleene ordinal, $\omega^{\mathrm{CK}}_1$, is a large countable ordinal. It is the smallest non-recursive ordinal. It is named after Alonzo Church and S. C. Kleene.

References

• Church, Alonzo; Kleene, S. C. (1937), "Formal definitions in the theory of ordinal numbers.", Fundamenta mathematicae, Warszawa, 28: 11–21, JFM 63.0029.02 
• Church, Alonzo (1938), "The constructive second number class", Bull. Amer. Math. Soc. 44 (4): 224–232, doi:10.1090/S0002-9904-1938-06720-1, http://www.ams.org/bull/1938-44-04/S0002-9904-1938-06720-1/ 
• Kleene, S. C. (1938), "On Notation for Ordinal Numbers", The Journal of Symbolic Logic (The Journal of Symbolic Logic, Vol. 3, No. 4) 3 (4): 150–155, doi:10.2307/2267778, JSTOR 2267778 
• Rogers, Hartley (1987) [1967], The Theory of Recursive Functions and Effective Computability, First MIT press paperback edition, ISBN 978-0-262-68052-3 

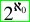
This set theory-related article is a stub. You can help Wikipedia by expanding it.v · Categories: Proof theory Ordinal numbers Set theory stubs Wikimedia Foundation. 2010. Игры ⚽ Нужно решить контрольную? Eastern Suburbs season 1932 Model Aviation Look at other dictionaries: Kleene's O — In set theory and computability theory, Kleene s mathcal{O} is a canonical subset of the natural numbers when regarded as ordinal notations. It contains ordinal notations for every recursive ordinal, that is, ordinals below Church–Kleene ordinal …   Wikipedia Ordinal notation — In mathematical logic and set theory, an ordinal notation is a finite sequence of symbols from a finite alphabet which names an ordinal number according to some scheme which gives meaning to the language. There are many such schemes of ordinal… …   Wikipedia Ordinal number — This article is about the mathematical concept. For number words denoting a position in a sequence ( first , second , third , etc.), see Ordinal number (linguistics). Representation of the ordinal numbers up to ωω. Each turn of the spiral… …   Wikipedia Ordinal analysis — In proof theory, ordinal analysis assigns ordinals (often large countable ordinals) to mathematical theories as a measure of their strength. The field was formed when Gerhard Gentzen in 1934 used cut elimination to prove, in modern terms, that… …   Wikipedia Ordinal collapsing function — In mathematical logic and set theory, an ordinal collapsing function (or projection function) is a technique for defining (notations for) certain recursive large countable ordinals, whose principle is to give names to certain ordinals much larger …   Wikipedia Large countable ordinal — In the mathematical discipline of set theory, there are many ways of describing specific countable ordinals. The smallest ones can be usefully and non circularly expressed in terms of their Cantor normal forms. Beyond that, many ordinals of… …   Wikipedia Church–Turing thesis — Church s thesis redirects here. For the constructive mathematics assertion, see Church s thesis (constructive mathematics). In computability theory, the Church–Turing thesis (also known as the Church–Turing conjecture, Church s thesis, Church s… …   Wikipedia Admissible ordinal — In set theory, an admissible ordinal is any ordinal number α such that Lα is a standard set model of Kripke–Platek set theory. In this case, Lα is said to be an admissible set.The first two admissible ordinals are ω and omega 1^{mathrm{CK (the… …   Wikipedia Recursive ordinal — In mathematics, specifically set theory, an ordinal α is said to be recursive if there is a recursive binary relation R that well orders a subset of the natural numbers and the order type of that ordering is α. It is trivial to check that ω is… …   Wikipedia Kleene's recursion theorem — In computability theory, Kleene s recursion theorems are a pair of fundamental results about the application of computable functions to their own descriptions. The theorems were first proved by Stephen Kleene in 1938.This article uses the… …   Wikipedia 18+ © Academic, 2000-2025 Contact us: Technical Support, Advertising Dictionaries export, created on PHP, Joomla, Drupal, WordPress, MODx. Mark and share Search through all dictionaries Translate… Search Internet Share the article and excerpts Direct link … Do a right-click on the link above and select “Copy Link”