- Cycle detection
-
This article is about iterated functions. For another use, see Cycle detection (graph theory).
In computer science, cycle detection is the algorithmic problem of finding a cycle in a sequence of iterated function values.
For any function ƒ that maps a finite set S to itself, and any initial value x0 in S, the sequence of iterated function values
must eventually use the same value twice: there must be some i ≠ j such that xi = xj. Once this happens, the sequence must continue by repeating the cycle of values from xi to xj−1. Cycle detection is the problem of finding i and j, given ƒ and x0.
Contents
Example
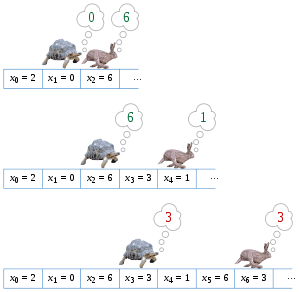
The figure shows a function ƒ that maps the set S = {0,1,2,3,4,5,6,7,8} to itself. If one starts from x0 = 2 and repeatedly applies ƒ, one sees the sequence of values
- 2, 0, 6, 3, 1, 6, 3, 1, 6, 3, 1, ....
The cycle to be detected is the repeating subsequence of values 6, 3, 1 in this sequence.
Definitions
Let S be any finite set, ƒ be any function from S to itself, and x0 be any element of S. For any i > 0, let xi = ƒ(xi−1). Let μ be the smallest index such that the value xμ reappears infinitely often within the sequence of values xi, and let λ (the loop length) be the smallest positive integer such that xμ = xλ+μ. The cycle detection problem is the task of finding λ and μ.
One can view the same problem graph-theoretically, by constructing a functional graph (that is, a directed graph in which each vertex has a single outgoing edge) the vertices of which are the elements of S and the edges of which map an element to the corresponding function value, as shown in the figure. The set of vertices reachable from any starting vertex x0 form a subgraph with a shape resembling the Greek letter rho (ρ): a path of length μ from x0 to a cycle of λ vertices.
Computer representation
Generally, ƒ will not be specified as a table of values, as we have given it in the figure above. Rather, we may be given access either to the sequence of values xi, or to a subroutine for calculating ƒ. The task is to find λ and μ while examining as few values from the sequence or performing as few subroutine calls as possible. Typically, also, the space complexity of an algorithm for the cycle detection problem is of importance: we wish to solve the problem while using an amount of memory significantly smaller than it would take to store the entire sequence.
In some applications, and in particular in Pollard's rho algorithm for integer factorization, the algorithm has much more limited access to S and to ƒ. In Pollard's rho algorithm, for instance, S is the set of integers modulo an unknown prime factor of the number to be factorized, so even the size of S is unknown to the algorithm. We may view a cycle detection algorithm for this application as having the following capabilities: it initially has in its memory an object representing a pointer to the starting value x0. At any step, it may perform one of three actions: it may copy any pointer it has to another object in memory, it may apply ƒ and replace any of its pointers by a pointer to the next object in the sequence, or it may apply a subroutine for determining whether two of its pointers represent equal values in the sequence. The equality test action may involve some nontrivial computation: in Pollard's rho algorithm, it is implemented by testing whether the difference between two stored values has a nontrivial gcd with the number to be factored. In this context, we will call an algorithm that only uses pointer copying, advancement within the sequence, and equality tests a pointer algorithm.
Algorithms
If the input is given as a subroutine for calculating ƒ, the cycle detection problem may be trivially solved using only λ+μ function applications, simply by computing the sequence of values xi and using a data structure such as a hash table to store these values and test whether each subsequent value has already been stored. However, the space complexity of this algorithm is λ+μ, unnecessarily large. Additionally, to implement this method as a pointer algorithm would require applying the equality test to each pair of values, resulting in quadratic time overall. Thus, research in this area has concentrated on two goals: using less space than this naive algorithm, and finding pointer algorithms that use fewer equality tests.
Tortoise and hare
Floyd's cycle-finding algorithm, also called the "tortoise and the hare" algorithm, is a pointer algorithm that uses only two pointers, which move through the sequence at different speeds. The algorithm is named for Robert W. Floyd, who invented it in the late 1960s.[1]
The key insight in the algorithm is that, for any integers i ≥ μ and k ≥ 0, xi = xi + kλ, where λ is the length of the loop to be found. In particular, whenever i = kλ ≥ μ, it follows that xi = x2i. Thus, the algorithm only needs to check for repeated values of this special form, one twice as far from the start of the sequence than the other, to find a period ν of a repetition that is a multiple of λ. Once ν is found, the algorithm retraces the sequence from its start to find the first repeated value xμ in the sequence, using the fact that λ divides ν and therefore that xμ = xν + μ. Finally, once the value of μ is known it is trivial to find the length λ of the shortest repeating cycle, by searching for the first position μ + λ for which xμ + λ = xμ.
The algorithm thus maintains two pointers into the given sequence, one (the tortoise) at xi, and the other (the hare) at x2i. At each step of the algorithm, it increases i by one, moving the tortoise one step forward and the hare two steps forward in the sequence, and then compares the sequence values at these two pointers. The smallest value of i > 0 for which the tortoise and hare point to equal values is the desired value ν.
The following Python code shows how this idea may be implemented as an algorithm.
def floyd(f, x0): # The main phase of the algorithm, finding a repetition x_mu = x_2mu # The hare moves twice as quickly as the tortoise tortoise = f(x0) # f(x0) is the element/node next to x0. hare = f(f(x0)) while tortoise != hare: tortoise = f(tortoise) hare = f(f(hare)) # at this point the start of the loop is equi-distant from current tortoise # position and x0, so hare moving in circle and tortoise (set to x0 ) # moving towards circle, will intersect at the beginning of the circle. # Find the position of the first repetition of length mu # The hare and tortoise move at the same speeds mu = 0 tortoise = x0 while tortoise != hare: tortoise = f(tortoise) hare = f(hare) mu += 1 # Find the length of the shortest cycle starting from x_mu # The hare moves while the tortoise stays still lam = 1 hare = f(tortoise) while tortoise != hare: hare = f(hare) lam += 1 return lam, mu
This code only accesses the sequence by storing and copying pointers, function evaluations, and equality tests; therefore, it qualifies as a pointer algorithm. The algorithm uses O(λ + μ) operations of these types, and O(1) storage space.
Brent's algorithm
Richard P. Brent described an alternative cycle detection algorithm that, like the tortoise and hare algorithm, requires only two pointers into the sequence.[2] However, it is based on a different principle: searching for the smallest power of two 2i that is larger than both λ and μ. For i = 0, 1, 2, etc., the algorithm compares x2i−1 with each subsequent sequence value up to the next power of two, stopping when it finds a match. It has two advantages compared to the tortoise and hare algorithm: it finds the correct length λ of the cycle directly, rather than needing to search for it in a subsequent stage, and its steps involve only one evaluation of ƒ rather than three.
The following Python code shows how this technique works in more detail.
def brent(f, x0): # main phase: search successive powers of two power = lam = 1 tortoise = x0 hare = f(x0) # f(x0) is the element/node next to x0. while tortoise != hare: if power == lam: # time to start a new power of two? tortoise = hare power *= 2 lam = 0 hare = f(hare) lam += 1 # Find the position of the first repetition of length lambda mu = 0 tortoise = hare = x0 for i in range(lam): # range(lam) produces a list with the values 0, 1, ... , lam-1 hare = f(hare) while tortoise != hare: tortoise = f(tortoise) hare = f(hare) mu += 1 return lam, mu
Like the tortoise and hare algorithm, this is a pointer algorithm that uses O(λ + μ) tests and function evaluations and O(1) storage space. It is not difficult to show that the number of function evaluations can never be higher than for Floyd's algorithm. Brent claims that, on average, his cycle finding algorithm runs around 36% more quickly than Floyd's and that it speeds up the Pollard rho algorithm by around 24%. He also performs an average case analysis for a randomized version of the algorithm in which the sequence of indices traced by the slower of the two pointers is not the powers of two themselves, but rather a randomized multiple of the powers of two. Although his main intended application was in integer factorization algorithms, Brent also discusses applications in testing pseudorandom number generators.
Time–space tradeoffs
A number of authors have studied techniques for cycle detection that use more memory than Floyd's and Brent's methods, but detect cycles more quickly. In general these methods store several previously-computed sequence values, and test whether each new value equals one of the previously-computed values. In order to do so quickly, they typically use a hash table or similar data structure for storing the previously-computed values, and therefore are not pointer algorithms: in particular, they usually cannot be applied to Pollard's rho algorithm. Where these methods differ is in how they determine which values to store. Following Nivasch,[3] we survey these techniques briefly.
- Brent[2] already describes variations of his technique in which the indices of saved sequence values are powers of a number R other than two. By choosing R to be a number close to one, and storing the sequence values at indices that are near a sequence of consecutive powers of R, a cycle detection algorithm can use a number of function evaluations that is within an arbitrarily small factor of the optimum λ+μ.[4][5]
- Sedgewick, Szymanski, and Yao[6] provide a method that uses M memory cells and requires in the worst case only (λ + μ)(1 + cM − 1 / 2) function evaluations, for some constant c, which they show to be optimal. The technique involves maintaining a numerical parameter d, storing in a table only those positions in the sequence that are multiples of d, and clearing the table and doubling d whenever too many values have been stored.
- Several authors have described distinguished point methods that store function values in a table based on a criterion involving the values, rather than (as in the method of Sedgewick et al.) based on their positions. For instance, values equal to zero modulo some value d might be stored.[7][8] More simply, Nivasch[3] credits D. P. Woodruff with the suggestion of storing a random sample of previously seen values, making an appropriate random choice at each step so that the sample remains random.
- Nivasch[3] describes an algorithm that does not use a fixed amount of memory, but for which the expected amount of memory used (under the assumption that the input function is random) is logarithmic in the sequence length. An item is stored in the memory table, with this technique, when no later item has a smaller value. As Nivasch shows, the items with this technique can be maintained using a stack data structure, and each successive sequence value need be compared only to the top of the stack. The algorithm terminates when the repeated sequence element with smallest value is found. Running the same algorithm with multiple stacks, using random permutations of the values to reorder the values within each stack, allows a time–space tradeoff similar to the previous algorithms. However, even the version of this algorithm with a single stack is not a pointer algorithm, due to the comparisons needed to determine which of two values is smaller.
Any cycle detection algorithm that stores at most M values from the input sequence must perform at least
 function evaluations.[9][10]
function evaluations.[9][10]Applications
Cycle detection has been used in many applications.
- Determining the cycle length of a pseudorandom number generator is one measure of its strength. This is the application cited by Knuth in describing Floyd's method. Brent[2] describes the results of testing a linear congruential generator in this fashion; its period turned out to be significantly smaller than advertised. For more complex generators, the sequence of values in which the cycle is to be found may not represent the output of the generator, but rather its internal state.
- Several number-theoretic algorithms are based on cycle detection, including Pollard's rho algorithm for integer factorization[11] and his related kangaroo algorithm for the discrete logarithm problem.[12]
- In cryptographic applications, the ability to find two distinct values xμ−-1 and xλ+μ−-1 mapped by some cryptographic function ƒ to the same value xμ may indicate a weakness in ƒ. For instance, Quisquater and Delescaille[8] apply cycle detection algorithms in the search for a message and a pair of Data Encryption Standard keys that map that message to the same encrypted value; Kaliski, Rivest, and Sherman[13] also use cycle detection algorithms to attack DES. The technique may also be used to find a collision in a cryptographic hash function.
- Cycle detection may be helpful as a way of discovering infinite loops in certain types of computer programs.[14]
- Periodic configurations in cellular automaton simulations may be found by applying cycle detection algorithms to the sequence of automaton states.[3]
- Shape analysis of linked list data structures is a technique for verifying the correctness of an algorithm using those structures. If a node in the list incorrectly points to an earlier node in the same list, the structure will form a cycle that can be detected by these algorithms.[15]
- Teske[5] describes applications in computational group theory: determining the structure of an Abelian group from a set of its generators. The cryptographic algorithms of Kaliski et al.[13] may also be viewed as attempting to infer the structure of an unknown group.
- Fich[9] briefly mentions an application to computer simulation of celestial mechanics, which she attributes to William Kahan. In this application, cycle detection in the phase space of an orbital system may be used to determine whether the system is periodic to within the accuracy of the simulation.
References
- ^ Floyd describes algorithms for listing all simple cycles in a directed graph in a 1967 paper: Floyd, R.W. (1967), "Non-deterministic Algorithms", J. ACM 14 (4): 636–644, doi:10.1145/321420.321422, http://doi.acm.org/10.1145/321420.321422. However this paper does not describe the cycle-finding problem in functional graphs that is the subject of this article. An early description of the tortoise and hare algorithm appears in Knuth, Donald E. (1969), The Art of Computer Programming, vol. II: Seminumerical Algorithms, Addison-Wesley, exercises 6 and 7, page 7. Knuth (p.4) credits Floyd for the algorithm, without citation.
- ^ a b c Brent, R. P. (1980), "An improved Monte Carlo factorization algorithm", BIT 20 (2): 176–184, doi:10.1007/BF01933190, http://wwwmaths.anu.edu.au/~brent/pd/rpb051i.pdf.
- ^ a b c d Nivasch, Gabriel (2004), "Cycle detection using a stack", Information Processing Letters 90 (3): 135–140, doi:10.1016/j.ipl.2004.01.016.
- ^ Schnorr, Claus P.; Lenstra, Hendrik W. (1984), "A Monte Carlo Factoring Algorithm With Linear Storage", Mathematics of Computation (American Mathematical Society) 43 (167): 289–311, doi:10.2307/2007414, JSTOR 2007414.
- ^ a b Teske, Edlyn (1998), "A space-efficient algorithm for group structure computation", Mathematics of Computation 67 (224): 1637–1663, doi:10.1090/S0025-5718-98-00968-5.
- ^ Sedgewick, Robert; Szymanski, Thomas G.; Yao, Andrew C.-C. (1982), "The complexity of finding cycles in periodic functions", SIAM Journal on Computing 11 (2): 376–390, doi:10.1137/0211030.
- ^ van Oorschot, Paul C.; Wiener, Michael J. (1999), "Parallel collision search with cryptanalytic applications", Journal of Cryptology 12 (1): 1–28, doi:10.1007/PL00003816.
- ^ a b Quisquater, J.-J.; Delescaille, J.-P., "How easy is collision search? Application to DES", Advances in Cryptology – EUROCRYPT '89, Workshop on the Theory and Application of Cryptographic Techniques, Lecture Notes in Computer Science, 434, Springer-Verlag, pp. 429–434, http://www.springerlink.com/content/0wnq56dava5nnm17/.
- ^ a b Fich, Faith Ellen (1981), "Lower bounds for the cycle detection problem", Proc. 13th ACM Symp. Theory of Computation, pp. 96–105, doi:10.1145/800076.802462.
- ^ Allender, Eric W.; Klawe, Maria M. (1985), "Improved lower bounds for the cycle detection problem", Theoretical Computer Science 36 (2–3): 231–237, doi:10.1016/0304-3975(85)90044-1.
- ^ Pollard, J. M. (1975), "A Monte Carlo method for factorization", BIT 15 (3): 331–334, doi:10.1007/BF01933667.
- ^ Pollard, J. M. (1978), "Monte Carlo methods for index computation (mod p)", Math. Comp. (American Mathematical Society) 32 (143): 918–924, doi:10.2307/2006496, JSTOR 2006496.
- ^ a b Kaliski, Burton S., Jr.; Rivest, Ronald L.; Sherman, Alan T. (1988), "Is the Data Encryption Standard a group? (Results of cycling experiments on DES)", Journal of Cryptology 1 (1): 3–36, doi:10.1007/BF00206323.
- ^ Van Gelder, Allen (1987), "Efficient loop detection in Prolog using the tortoise-and-hare technique", Journal of Logic Programming 4 (1): 23–31, doi:10.1016/0743-1066(87)90020-3.
- ^ Auguston, Mikhail; Hon, Miu Har (1997), "Assertions for Dynamic Shape Analysis of List Data Structures", AADEBUG '97, Proceedings of the Third International Workshop on Automatic Debugging, Linköping Electronic Articles in Computer and Information Science, Linköping University, pp. 37–42, http://www.ep.liu.se/ea/cis/1997/009/04/.
External links
- Gabriel Nivasch, The Cycle Detection Problem and the Stack Algorithm.
- Tortoise and Hare, Portland Pattern Repository
Categories:- Fixed points
- Combinatorial algorithms
Wikimedia Foundation. 2010.