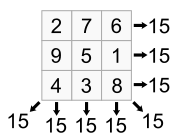
- Magic square
-
In recreational mathematics, a magic square of order n is an arrangement of n2 numbers, usually distinct integers, in a square, such that the n numbers in all rows, all columns, and both diagonals sum to the same constant.[1] A normal magic square contains the integers from 1 to n2. The term "magic square" is also sometimes used to refer to any of various types of word square.
Normal magic squares exist for all orders n ≥ 1 except n = 2, although the case n = 1 is trivial, consisting of a single cell containing the number 1. The smallest nontrivial case, shown below, is of order 3.
The constant sum in every row, column and diagonal is called the magic constant or magic sum, M. The magic constant of a normal magic square depends only on n and has the value
For normal magic squares of order n = 3, 4, 5, ..., the magic constants are:
History
 Iron plate with an order 6 magic square in Arabic numbers from China, dating to the Yuan Dynasty (1206-1368).
Iron plate with an order 6 magic square in Arabic numbers from China, dating to the Yuan Dynasty (1206-1368).
Magic squares were known to Chinese mathematicians, as early as 650 BCE[2] and Arab mathematicians, possibly as early as the 7th century, when the Arabs conquered northwestern parts of the Indian subcontinent and learned Indian mathematics and astronomy, including other aspects of combinatorial mathematics.[citation needed] The first magic squares of order 5 and 6 appear in an encyclopedia from Baghdad circa 983 CE, the Encyclopedia of the Brethren of Purity (Rasa'il Ihkwan al-Safa); simpler magic squares were known to several earlier Arab mathematicians.[2] Some of these squares were later used in conjunction with magic letters as in (Shams Al-ma'arif) to assist Arab illusionists and magicians.[3]
Lo Shu square (3×3 magic square)
Main article: Lo Shu SquareChinese literature dating from as early as 650 BC tells the legend of Lo Shu or "scroll of the river Lo".[2] In ancient China there was a huge flood. The great king Yu (禹) tried to channel the water out to sea where then emerged from the water a turtle with a curious figure/pattern on its shell; circular dots of numbers which were arranged in a three by three grid pattern such that the sum of the numbers in each row, column and diagonal was the same: 15, which is also the number of days in each of the 24 cycles of the Chinese solar year. This pattern, in a certain way, was used by the people in controlling the river.
4 9 2 3 5 7 8 1 6 The Lo Shu Square, as the magic square on the turtle shell is called, is the unique normal magic square of order three in which 1 is at the bottom and 2 is in the upper right corner. Every normal magic square of order three is obtained from the Lo Shu by rotation or reflection.
The Square of Lo Shu is also referred to as the Magic Square of Saturn or Chronos.
Cultural significance
Magic squares have fascinated humanity throughout the ages, and have been around for over 4,120 years. They are found in a number of cultures, including Egypt and India, engraved on stone or metal and worn as talismans, the belief being that magic squares had astrological and divinatory qualities, their usage ensuring longevity and prevention of diseases.
The Kubera-Kolam is a floor painting used in India which is in the form of a magic square of order three. It is essentially the same as the Lo Shu Square, but with 19 added to each number, giving a magic constant of 72.
23 28 21 22 24 26 27 20 25 Persia
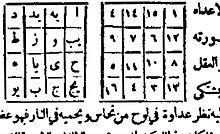 Printed version of the previous manuscript. Eastern Arabic numerals were used.
Printed version of the previous manuscript. Eastern Arabic numerals were used.
Although a definitive judgement of early history of magic squares is not available, it has been suggested that magic squares are probably of pre-Islamic Persian origin.[4] The study of magic squares in medieval Islam in Persia is however common, and supposedly, came after the introduction of Chess in Persia.[5] For instance in the tenth century, the Persian mathematician Buzjani has left a manuscript on page 33 of which there is a series of magic squares, which are filled by numbers in arithmetic progression in such a way that the sums on each line, column and diagonal are equal.[6]
Arabia
Magic squares were known to Islamic mathematicians, possibly as early as the 7th century, when the Arabs came into contact with Indian culture, and learned Indian mathematics and astronomy, including other aspects of combinatorial mathematics. It has also been suggested that the idea came via China. The first magic squares of order 5 and 6 appear in an encyclopedia from Baghdad circa 983 AD, the Rasa'il Ikhwan al-Safa (the Encyclopedia of the Brethren of Purity); simpler magic squares were known to several earlier Arab mathematicians.[2]
The Arab mathematician Ahmad al-Buni, who worked on magic squares around 1250 A.D., attributed mystical properties to them, although no details of these supposed properties are known. There are also references to the use of magic squares in astrological calculations, a practice that seems to have originated with the Arabs.[2]
India
The 3x3 magic square was used as part of rituals in India from vedic times, and continues to be used to date.The Ganesh yantra is a 3x3 magic square. A well known early 4x4 magic square in India can be seen in Khajuraho in the Parshvanath Jain temple. It dates from the 10th century.[7]
7 12 1 14 2 13 8 11 16 3 10 5 9 6 15 4 This is referred to as the Chautisa Yantra, since each row, column, diagonal, 2x2 sub-square, the corners of each 3x3 and 4x4 square, the two sets of four symmetrical numbers (1+11+16+6 and 2+12+15+5), and the sum of the middle two entries of the two outer columns and rows (12+1+6+15 and 2+16+11+5), sums to 34.
Europe
 This page from Athanasius Kircher's Oedipus Aegyptiacus (1653) belongs to a treatise on magic squares and shows the Sigillum Iovis associated with Jupiter
This page from Athanasius Kircher's Oedipus Aegyptiacus (1653) belongs to a treatise on magic squares and shows the Sigillum Iovis associated with Jupiter
In 1300, building on the work of the Arab Al-Buni, Greek Byzantine scholar Manuel Moschopoulos wrote a mathematical treatise on the subject of magic squares, leaving out the mysticism of his predecessors.[8] Moschopoulos is thought to be the first Westerner to have written on the subject. In the 1450s the Italian Luca Pacioli studied magic squares and collected a large number of examples.[2]
In about 1510 Heinrich Cornelius Agrippa wrote De Occulta Philosophia, drawing on the Hermetic and magical works of Marsilio Ficino and Pico della Mirandola, and in it he expounded on the magical virtues of seven magical squares of orders 3 to 9, each associated with one of the astrological planets. This book was very influential throughout Europe until the counter-reformation, and Agrippa's magic squares, sometimes called Kameas, continue to be used within modern ceremonial magic in much the same way as he first prescribed.[2][9]
Saturn=15 4 9 2 3 5 7 8 1 6 Jupiter=34 4 14 15 1 9 7 6 12 5 11 10 8 16 2 3 13 Mars=65 11 24 7 20 3 4 12 25 8 16 17 5 13 21 9 10 18 1 14 22 23 6 19 2 15 Sol=111 6 32 3 34 35 1 7 11 27 28 8 30 19 14 16 15 23 24 18 20 22 21 17 13 25 29 10 9 26 12 36 5 33 4 2 31 Venus=175 22 47 16 41 10 35 4 5 23 48 17 42 11 29 30 6 24 49 18 36 12 13 31 7 25 43 19 37 38 14 32 1 26 44 20 21 39 8 33 2 27 45 46 15 40 9 34 3 28 Mercury=260 8 58 59 5 4 62 63 1 49 15 14 52 53 11 10 56 41 23 22 44 45 19 18 48 32 34 35 29 28 38 39 25 40 26 27 37 36 30 31 33 17 47 46 20 21 43 42 24 9 55 54 12 13 51 50 16 64 2 3 61 60 6 7 57 Luna=369 37 78 29 70 21 62 13 54 5 6 38 79 30 71 22 63 14 46 47 7 39 80 31 72 23 55 15 16 48 8 40 81 32 64 24 56 57 17 49 9 41 73 33 65 25 26 58 18 50 1 42 74 34 66 67 27 59 10 51 2 43 75 35 36 68 19 60 11 52 3 44 76 77 28 69 20 61 12 53 4 45 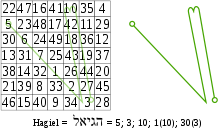 The derivation of the sigil of Hagiel, the planetary intelligence of Venus, drawn on the magic square of Venus. Each Hebrew letter provides a numerical value, giving the vertices of the sigil.
The derivation of the sigil of Hagiel, the planetary intelligence of Venus, drawn on the magic square of Venus. Each Hebrew letter provides a numerical value, giving the vertices of the sigil.
The most common use for these Kameas is to provide a pattern upon which to construct the sigils of spirits, angels or demons; the letters of the entity's name are converted into numbers, and lines are traced through the pattern that these successive numbers make on the kamea. In a magical context, the term magic square is also applied to a variety of word squares or number squares found in magical grimoires, including some that do not follow any obvious pattern, and even those with differing numbers of rows and columns. They are generally intended for use as talismans. For instance the following squares are: The Sator square, one of the most famous magic squares found in a number of grimoires including the Key of Solomon; a square "to overcome envy", from The Book of Power;[10] and two squares from The Book of the Sacred Magic of Abramelin the Mage, the first to cause the illusion of a superb palace to appear, and the second to be worn on the head of a child during an angelic invocation:
S A T O R A R E P O T E N E T O P E R A R O T A S 6 66 848 938 8 11 544 839 1 11 383 839 2 73 774 447 H E S E B E Q A L S E G B A D A M D A R A A R A D M A D A Albrecht Dürer's magic square
The order-4 magic square in Albrecht Dürer's engraving Melencolia I is believed to be the first seen in European art. It is very similar to Yang Hui's square, which was created in China about 250 years before Dürer's time. The sum 34 can be found in the rows, columns, diagonals, each of the quadrants, the center four squares, and the corner squares(of the 4x4 as well as the four contained 3x3 grids). This sum can also be found in the four outer numbers clockwise from the corners (3+8+14+9) and likewise the four counter-clockwise (the locations of four queens in the two solutions of the 4 queens puzzle [11]), the two sets of four symmetrical numbers (2+8+9+15 and 3+5+12+14), the sum of the middle two entries of the two outer columns and rows (5+9+8+12 and 3+2+15+14), and in four kite or cross shaped quartets(3+5+11+15, 2+10+8+14, 3+9+7+15, and 2+6+12+14). The two numbers in the middle of the bottom row give the date of the engraving: 1514. The numbers 1 and 4 at either side of the date correspond to, in English, the letters 'A' and 'D' which are the initials of the artist.
16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1 Dürer's magic square can also be extended to a magic cube.[12]
Dürer's magic square and his Melencolia I both also played large roles in Dan Brown's 2009 novel, The Lost Symbol.
Sagrada Família magic square
The Passion façade of the Sagrada Família church in Barcelona, designed by sculptor Josep Subirachs, features a 4×4 magic square:
The magic constant of the square is 33, the age of Jesus at the time of the Passion. Structurally, it is very similar to the Melancholia magic square, but it has had the numbers in four of the cells reduced by 1.
1 14 14 4 11 7 6 9 8 10 10 5 13 2 3 15 While having the same pattern of summation, this is not a normal magic square as above, as two numbers (10 and 14) are duplicated and two (12 and 16) are absent, failing the 1→n2 rule.
Similarly to Dürer's magic square, the Sagrada Familia's magic square can also be extended to a magic cube.[13]
Types and construction
There are many ways to construct magic squares, but the standard (and most simple) way is to follow certain configurations/formulas which generate regular patterns. Magic squares exist for all values of n, with only one exception: it is impossible to construct a magic square of order 2. Magic squares can be classified into three types: odd, doubly even (n divisible by four) and singly even (n even, but not divisible by four). Odd and doubly even magic squares are easy to generate; the construction of singly even magic squares is more difficult but several methods exist, including the LUX method for magic squares (due to John Horton Conway) and the Strachey method for magic squares.
Group theory was also used for constructing new magic squares of a given order from one of them, please see.[14]
Unsolved problems in mathematics How many n×n magic squares for n>5? 
The number of different n×n magic squares for n from 1 to 5, not counting rotations and reflections:
The number for n = 6 has been estimated to 1.7745×1019.
Method for constructing a magic square of odd order
See also: Siamese methodYang Hui's construction method
A method for constructing magic squares of odd order was published by the French diplomat de la Loubère in his book A new historical relation of the kingdom of Siam (Du Royaume de Siam, 1693), under the chapter entitled The problem of the magical square according to the Indians.[15] The method operates as follows:
Starting from the central column of the first row with the number 1, the fundamental movement for filling the squares is diagonally up and right, one step at a time. If a filled square is encountered, one moves vertically down one square instead, then continuing as before. When a move would leave the square, it is wrapped around to the last row or first column, respectively.
step 1 1 . . step 2 1 . 2 step 3 1 3 2 step 4 1 3 4 2 step 5 1 3 5 4 2 step 6 1 6 3 5 4 2 step 7 1 6 3 5 7 4 2 step 8 8 1 6 3 5 7 4 2 step 9 8 1 6 3 5 7 4 9 2 Starting from other squares rather than the central column of the first row is possible, but then only the row and column sums will be identical and result in a magic sum, whereas the diagonal sums will differ. The result will thus be a semimagic square and not a true magic square. Moving in directions other than north east can also result in magic squares.
Order 3 8 1 6 3 5 7 4 9 2 Order 5 17 24 1 8 15 23 5 7 14 16 4 6 13 20 22 10 12 19 21 3 11 18 25 2 9 Order 9 47 58 69 80 1 12 23 34 45 57 68 79 9 11 22 33 44 46 67 78 8 10 21 32 43 54 56 77 7 18 20 31 42 53 55 66 6 17 19 30 41 52 63 65 76 16 27 29 40 51 62 64 75 5 26 28 39 50 61 72 74 4 15 36 38 49 60 71 73 3 14 25 37 48 59 70 81 2 13 24 35 The following formulae help construct magic squares of odd order
Order n Squares (n) Last No. Middle No. Sum (M) Ith row and Jth column No. n n2 


Example:
Order 5 Squares (n) Last No. Middle No. Sum (M) 5 25 13 65 The "Middle Number" is always in the diagonal bottom left to top right.
The "Last Number" is always opposite the number 1 in an outside column or row.A method of constructing a magic square of doubly even order
Doubly even means that n is an even multiple of an even integer; or 4p (e.g. 4, 8, 12), where p is an integer.
Generic pattern All the numbers are written in order from left to right across each row in turn, starting from the top left hand corner. The resulting square is also known as a mystic square. Numbers are then either retained in the same place or interchanged with their diametrically opposite numbers in a certain regular pattern. In the magic square of order four, the numbers in the four central squares and one square at each corner are retained in the same place and the others are interchanged with their diametrically opposite numbers.
A construction of a magic square of order 4 Go left to right through the square filling counting and filling in on the diagonals only. Then continue by going left to right from the top left of the table and fill in counting down from 16 to 1. As shown below.
M = Order 4 1 4 6 7 10 11 13 16 M = Order 4 1 15 14 4 12 6 7 9 8 10 11 5 13 3 2 16 An extension of the above example for Orders 8 and 12 First generate a "truth" table, where a '1' indicates selecting from the square where the numbers are written in order 1 to n2 (left-to-right, top-to-bottom), and a '0' indicates selecting from the square where the numbers are written in reverse order n2 to 1. For M = 4, the "truth" table is as shown below, (third matrix from left.)
M = Order 4 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 M = Order 4 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 M = Order 4 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 M = Order 4 1 15 14 4 12 6 7 9 8 10 11 5 13 3 2 16 Note that a) there are equal number of '1's and '0's; b) each row and each column are "palindromic"; c) the left- and right-halves are mirror images; and d) the top- and bottom-halves are mirror images (c & d imply b.) The truth table can be denoted as (9, 6, 6, 9) for simplicity (1-nibble per row, 4 rows.) Similarly, for M=8, two choices for the truth table are (A5, 5A, A5, 5A, 5A, A5, 5A, A5) or (99, 66, 66, 99, 99, 66, 66, 99) (2-nibbles per row, 8 rows.) For M=12, the truth table (E07, E07, E07, 1F8, 1F8, 1F8, 1F8, 1F8, 1F8, E07, E07, E07) yields a magic square (3-nibbles per row, 12 rows.) It is possible to count the number of choices one has based on the truth table, taking rotational symmetries into account.
Medjig-method of constructing magic squares of even number of rows
This method is based on a 2006 published mathematical game called medjig (author: Willem Barink, editor: Philos-Spiele). The pieces of the medjig puzzle are squares divided in four quadrants on which the numbers 0, 1, 2 and 3 are dotted in all sequences. There are 18 squares, with each sequence occurring 3 times. The aim of the puzzle is to take 9 squares out of the collection and arrange them in a 3 x 3 "medjig-square" in such a way that each row and column formed by the quadrants sums to 9, along with the two long diagonals.
The medjig method of constructing a magic square of order 6 is as follows:
- Construct any 3 x 3 medjig-square (ignoring the original game's limit on the number of times that a given sequence is used).
- Take the 3 x 3 magic square and divide each of its squares into four quadrants.
- Fill these quadrants with the four numbers from 1 to 36 that equal the original number modulo 9, i.e. x+9y where x is the original number and y is a number from 0 to 3, following the pattern of the medjig-square.
Example:
Order 3 8 1 6 3 5 7 4 9 2 Medjig 3 x 3 2 3 0 2 0 2 1 0 3 1 3 1 3 1 1 2 2 0 0 2 0 3 3 1 3 2 2 0 0 2 0 1 3 1 1 3 Order 6 26 35 1 19 6 24 17 8 28 10 33 15 30 12 14 23 25 7 3 21 5 32 34 16 31 22 27 9 2 20 4 13 36 18 11 29 Similarly, for any larger integer N, a magic square of order 2N can be constructed from any N x N medjig-square with each row, column, and long diagonal summing to 3N, and any N x N magic square (using the four numbers from 1 to 4N^2 that equal the original number modulo N^2).
Construction of panmagic squares
Any number p in the order-n square can be uniquely written in the form p = an + r, with r chosen from {1,...,n}. Note that due to this restriction, a and r are not the usual quotient and remainder of dividing p by n. Consequently the problem of constructing can be split in two problems easier to solve. So, construct two matching square grids of order n satisfying panmagic properties, one for the a-numbers (0,..., n−1), and one for the r-numbers (1,...,n). This requires a lot of puzzling, but can be done. When successful, combine them into one panmagic square. Van den Essen and many others supposed this was also the way Benjamin Franklin (1706–1790) constructed his famous Franklin squares. Three panmagic squares are shown below. The first two squares have been constructed April 2007 by Barink, the third one is some years older, and comes from Donald Morris, who used, as he supposes, the Franklin way of construction.
Order 8, sum 260 62 4 13 51 46 20 29 35 5 59 54 12 21 43 38 28 52 14 3 61 36 30 19 45 11 53 60 6 27 37 44 22 64 2 15 49 48 18 31 33 7 57 56 10 23 41 40 26 50 16 1 63 34 32 17 47 9 55 58 8 25 39 42 24 Order 12, sum 870 138 8 17 127 114 32 41 103 90 56 65 79 19 125 140 6 43 101 116 30 67 77 92 54 128 18 7 137 104 42 31 113 80 66 55 89 5 139 126 20 29 115 102 44 53 91 78 68 136 10 15 129 112 34 39 105 88 58 63 81 21 123 142 4 45 99 118 28 69 75 94 52 130 16 9 135 106 40 33 111 82 64 57 87 3 141 124 22 27 117 100 46 51 93 76 70 134 12 13 131 110 36 37 107 86 60 61 83 23 121 144 2 47 97 120 26 71 73 96 50 132 14 11 133 108 38 35 109 84 62 59 85 1 143 122 24 25 119 98 48 49 95 74 72 Order 12, sum 870 1 120 121 48 85 72 73 60 97 24 25 144 142 27 22 99 58 75 70 87 46 123 118 3 11 110 131 38 95 62 83 50 107 14 35 134 136 33 16 105 52 81 64 93 40 129 112 9 8 113 128 41 92 65 80 53 104 17 32 137 138 31 18 103 54 79 66 91 42 127 114 7 5 116 125 44 89 68 77 56 101 20 29 140 139 30 19 102 55 78 67 90 43 126 115 6 12 109 132 37 96 61 84 49 108 13 36 133 135 34 15 106 51 82 63 94 39 130 111 10 2 119 122 47 86 71 74 59 98 23 26 143 141 28 21 100 57 76 69 88 45 124 117 4 The order 8 square satisfies all panmagic properties, including the Franklin ones. It consists of 4 perfectly panmagic 4x4 units. Note that both order 12 squares show the property that any row or column can be divided in three parts having a sum of 290 (= 1/3 of the total sum of a row or column). This property compensates the absence of the more standard panmagic Franklin property that any 1/2 row or column shows the sum of 1/2 of the total. For the rest the order 12 squares differ a lot.The Barink 12x12 square is composed of 9 perfectly panmagic 4x4 units, moreover any 4 consecutive numbers starting on any odd place in a row or column show a sum of 290. The Morris 12x12 square lacks these properties, but on the contrary shows constant Franklin diagonals. For a better understanding of the constructing decompose the squares as described above, and see how it was done. And note the difference between the Barink constructions on the one hand, and the Morris/Franklin construction on the other hand.
In the book Mathematics in the Time-Life Science Library Series, magic squares by Euler and Franklin are shown. Franklin designed this one so that any four-square subset (any four contiguous squares that form a larger square, or any four squares equidistant from the center) total 130. In Euler's square, the rows and columns each total 260, and halfway they total 130—and a chess knight, making its L-shaped moves on the square, can touch all 64 boxes in consecutive numerical order.
Construction similar to the Kronecker Product
There is a method reminiscent of the Kronecker product of two matrices, that builds an nm x nm magic square from an n x n magic square and an m x m magic square.[16]
The construction of a magic square using genetic algorithms
A magic square can be constructed using genetic algorithms.[17] In this process an initial population of magic squares with random values are generated. The fitness scores of these individual magic squares are calculated based on the degree of deviation in the sums of the rows, columns, and diagonals. The population of magic squares reproduce by exchanging values, together with some random mutations. Those squares with a higher fitness score are more likely to reproduce. The next generation of the magic square population is again calculated for their fitness, and this process continues until a solution has been found or a time limit has been reached.
Generalizations
Extra constraints
Certain extra restrictions can be imposed on magic squares. If not only the main diagonals but also the broken diagonals sum to the magic constant, the result is a panmagic square. If raising each number to certain powers yields another magic square, the result is a bimagic, a trimagic, or, in general, a multimagic square.
Different constraints
Sometimes the rules for magic squares are relaxed, so that only the rows and columns but not necessarily the diagonals sum to the magic constant (this is usually called a semimagic square).
In heterosquares and antimagic squares, the 2n + 2 sums must all be different.
Multiplicative magic squares
Instead of adding the numbers in each row, column and diagonal, one can apply some other operation. For example, a multiplicative magic square has a constant product of numbers. A multiplicative magic square can be derived from an additive magic square by raising 2 (or any other integer) to the power of each element. For example, the original Lo-Shu magic square becomes:
M = 32768 16 512 4 8 32 128 256 2 64 Other examples of multiplicative magic squares include:
M = 216 2 9 12 36 6 1 3 4 18 M = 6720 1 6 20 56 40 28 2 3 14 5 24 4 12 8 7 10 Ali Skalli's non iterative method of construction is also applicable to multiplicative magic squares. On the 7x7 example below, the products of each line, each column and each diagonal is 6,227,020,800.
Skalli multiplicative 7 x 7 27 50 66 84 13 2 32 24 52 3 40 54 70 11 56 9 20 44 36 65 6 55 72 91 1 16 36 30 4 24 45 60 77 12 26 10 22 48 39 5 48 63 78 7 8 18 40 33 60 Multiplicative magic squares of complex numbers
Still using Ali Skalli's non iterative method, it is possible to produce an infinity of multiplicative magic squares of complex numbers[18] belonging to
 set. On the example below, the real and imaginary parts are integer numbers, but they can also belong to the entire set of real numbers
set. On the example below, the real and imaginary parts are integer numbers, but they can also belong to the entire set of real numbers  . The product is: −352,507,340,640 − 400,599,719,520 i.
. The product is: −352,507,340,640 − 400,599,719,520 i.Skalli multiplicative 7 x 7 of complex numbers 21+14i −70+30i −93−9i −105−217i 16+50i 4−14i 14−8i 63−35i 28+114i −14i 2+6i 3−11i 211+357i −123−87i 31−15i 13−13i −103+69i −261−213i 49−49i −46+2i −6+2i 102−84i −28−14i 43+247i −10−2i 5+9i 31−27i −77+91i −22−6i 7+7i 8+14i 50+20i −525−492i −28−42i −73+17i 54+68i 138−165i −56−98i −63+35i 4−8i 2−4i 70−53i 24+22i −46−16i 6−4i 17+20i 110+160i 84−189i 42−14i Other magic shapes
Other shapes than squares can be considered. The general case is to consider a design with N parts to be magic if the N parts are labeled with the numbers 1 through N and a number of identical sub-designs give the same sum. Examples include magic dodecahedrons, magic triangles[19] magic stars, and magic hexagons. Going up in dimension results in magic cubes, magic tesseracts and other magic hypercubes.
Edward Shineman has developed yet another design in the shape of magic diamonds.
Possible magic shapes are constrained by the number of equal-sized, equal-sum subsets of the chosen set of labels. For example, if one proposes to form a magic shape labeling the parts with {1, 2, 3, 4}, the sub-designs will have to be labeled with {1,4} and {2,3}.[19]
Other component elements
Magic squares may be constructed which contain geometric shapes rather than numbers, as in the "geomagic squares" introduced by Lee Sallows.[20]
Combined extensions
One can combine two or more of the above extensions, resulting in such objects as multiplicative multimagic hypercubes. Little seems to be known about this subject.
Related problems
Over the years, many mathematicians, including Euler, Cayley and Benjamin Franklin have worked on magic squares, and discovered fascinating relations.
Magic square of primes
Rudolf Ondrejka (1928–2001) discovered the following 3x3 magic square of primes, in this case nine Chen primes:
17 89 71 113 59 5 47 29 101 The Green–Tao theorem implies that there are arbitrarily large magic squares consisting of primes.
Using Ali Skalli's non-iterative method of magic squares construction, it is easy to create magic squares of primes[21] of any dimension. In the example below, many symmetries appear (including all sorts of crosses), as well as the horizontal and vertical translations of all those. The magic constant is 13665.
Skalli Primes 5 x 5 2087 2633 2803 2753 3389 2843 2729 3347 2099 2647 3359 2113 2687 2819 2687 2663 2777 2699 3373 2153 2713 3413 2129 2621 2789 It is believed that an infinite number of Skalli's magic squares of prime exist, but no demonstration exists to date. However, it is possible to easily produce a considerable number of them, not calculable in the absence of demonstration.
n-Queens problem
In 1992, Demirörs, Rafraf, and Tanik published a method for converting some magic squares into n-queens solutions, and vice versa.[22]
See also
- Arithmetic sequence
- Antimagic square
- Eight queens puzzle
- Freudenthal magic square
- Heterosquare
- Hexagonal tortoise problem
- Latin square
- Multimagic square (also known as a Satanic square)
- Magic series
- Magic cube
- Magic cube classes
- Magic star
- Magic tesseract
- Magic hypercube
- Most-perfect magic square
- Nasik magic hypercube
- Panmagic square (also known as a Diabolic square)
- Prime reciprocal magic square
- Room square
- Sator Arepo Tenet Opera Rotas
- Square matrices
- Sudoku
- Unsolved problems in mathematics
- Vedic square
- Word square
- Yang Hui
- John R. Hendricks
Notes
- ^ "Magic Square" by Onkar Singh, Wolfram Demonstrations Project.
- ^ a b c d e f g Swaney, Mark. [1].
- ^ The most famous Arabic book in magics, named "Shams Al-ma'arif (Arabic: كتاب شمس المعارف), for Ahmed bin Ali Al-boni who died about 1225 (622 AH).reprinted in Beirut in 1985
- ^ J. P. Hogendijk, A. I. Sabra, The Enterprise of Science in Islam: New Perspectives, Published by MIT Press, 2003, ISBN 0262194821, p. xv.
- ^ Helaine Selin, Ubiratan D'Ambrosio, Mathematics Across Cultures: The History of Non-western Mathematics, Published by Springer, 2001, ISBN 140200260, p. 160.
- ^ Sesiano, J., Abūal-Wafā\rasp's treatise on magic squares (french), Z. Gesch. Arab.-Islam. Wiss. 12 (1998), 121--244.
- ^ Magic Squares and Cubes By William Symes Andrews, 1908, Open court publish company
- ^ Manuel Moschopoulos - Mathematics and the Liberal Arts
- ^ Drury, Nevill (1992). Dictionary of Mysticism and the Esoteric Traditions. Bridport, Dorset: Prism Press. ISBN 1-85327-075-X.
- ^ "The Book of Power: Cabbalistic Secrets of Master Aptolcater, Mage of Adrianople", transl. 1724. In Shah, Idries (1957). The Secret Lore of Magic. London: Frederick Muller Ltd.
- ^ http://www.muljadi.org/MagicSquares.htm
- ^ "Magic cube with Dürer's square" Ali Skalli's magic squares and magic cubes
- ^ "Magic cube with Gaudi's square " Ali Skalli's magic squares and magic cubes
- ^ http://www.gaspalou.fr/magic-squares/index.htm
- ^ Mathematical Circles Squared" By Phillip E. Johnson, Howard Whitley Eves, p.22
- ^ Hartley, M. "Making Big Magic Squares".
- ^ Evolving a Magic Square using Genetic Algorithms
- ^ "8x8 multiplicative magic square of complex numbers" Ali Skalli's magic squares and magic cubes
- ^ a b Magic Designs,Robert B. Ely III, Journal of Recreational Mathematics volume 1 number 1, January 1968
- ^ Magic squares are given a whole new dimension, The Observer, April 3, 2011
- ^ "magic square of primes" Ali Skalli's magic squares and magic cubes
- ^ O. Demirörs, N. Rafraf, and M.M. Tanik. Obtaining n-queens solutions from magic squares and constructing magic squares from n-queens solutions. Journal of Recreational Mathematics, 24:272–280, 1992
References
- Weisstein, Eric W., "Magic Square" from MathWorld.
- Magic Squares at Convergence
- W. S. Andrews, Magic Squares and Cubes. (New York: Dover, 1960), originally printed in 1917
- John Lee Fults, Magic Squares. (La Salle, Illinois: Open Court, 1974).
- Cliff Pickover, The Zen of Magic Squares, Circles, and Stars (Princeton, New Jersey: Princeton University Press)
- Leonhard Euler, On magic squares ( pdf )
- Mark Farrar, Magic Squares ( [2] )
- Asker Ali Abiyev, The Natural Code of Numbered Magic Squares (1996), <http://www1.gantep.edu.tr/~abiyev/abiyeving.htm>
- William H. Benson and Oswald Jacoby, "New Recreations with Magic Squares". (New York: Dover, 1976).
- A 'perfect' magic square presented as a magic trick (Online Generator - Magic Square 4x4 using Javascript)
- Magic Squares of Order 4,5,6, and some theory
- Evolving a Magic Square using Genetic Algorithms
- Magic squares and magic cubes: examples of magic squares and magic cubes built with Ali Skalli's non iterative method
Further reading
- Charney, Noah The Art Thief Atria (2007), a novel with a key plot point involving a magic square.
- McCranie, Judson (November 1988). "Magic Squares of All Orders". Mathematics Teacher: 674–78.
- King, J. R. (1963). Magic Square Numbers.
- Magic square at the Open Directory Project
Categories:- Recreational mathematics
- Magic squares
- Matrices
- Unsolved problems in mathematics
- Magic (paranormal)
Wikimedia Foundation. 2010.