Formal concept analysis

Formal concept analysis is a principled way of automatically deriving an ontology from a collection of objects and their properties. The term was introduced by Rudolf Wille in 1984, and builds on applied lattice and order theory that was developed by Birkhoff and others in the 1930s.

Intuitive description

Formal concept analysis refers to both an unsupervised machine learning technique and, more broadly, a method of data analysis. The approach takes as input a matrix specifying a set of objects and the properties thereof, called attributes, and finds both all the "natural" clusters of attributes and all the "natural" clusters of objects in the input data, where

• a "natural" object cluster is the set of all objects that share a common subset of attributes, and
• a "natural" property cluster is the set of all attributes shared by one of the natural object clusters.

Natural property clusters correspond one-for-one with natural object clusters, and a concept is a pair containing both a natural property cluster and its corresponding natural object cluster. The family of these concepts obeys the mathematical axioms defining a lattice, and is called a concept lattice (in French this is called a Treillis de Galois because the relation between the sets of concepts and attributes is a Galois connection).

Note the strong parallel between "natural" property clusters and definitions in terms of individually necessary and jointly sufficient conditions, on one hand, and between "natural" object clusters and the extensions of such definitions, on the other. Provided that the input objects and input concepts provide a complete description of the world (never true in practice, but perhaps a reasonable approximation), then the set of attributes in each concept can be interpreted as a set of singly necessary and jointly sufficient conditions for defining the set of objects in the concept. Conversely, if a set of attributes is not identified as a concept in this framework, then those attributes are not singly necessary and jointly sufficient for defining any non-empty subset of objects in the world.

Example

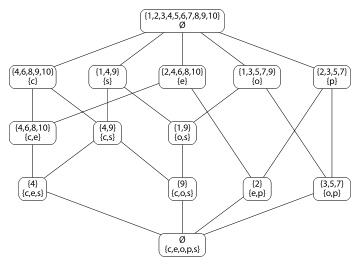A concept lattice for objects consisting of the integers from 1 to 10, and attributes composite (c), square (s), even (e), odd (o) and prime (p). The lattice is drawn as a Hasse diagram.

Consider O = {1,2,3,4,5,6,7,8,9,10}, and A = {composite, even, odd, prime, square}. The smallest concept including the number 3 is the one with objects {3,5,7}, and attributes {odd, prime}, for 3 has both of those attributes and {3,5,7} is the set of objects having that set of attributes. The largest concept involving the attribute of being square is the one with objects {1,4,9} and attributes {square}, for 1, 4 and 9 are all the square numbers and all three of them have that set of attributes. It can readily be seen that both of these example concepts satisfy the formal definitions below

The full set of concepts for these objects and attributes is shown in the illustration. It includes a concept for each of the original attributes: the composite numbers, square numbers, even numbers, odd numbers, and prime numbers. Additionally it includes concepts for the even composite numbers, composite square numbers (that is, all square numbers except 1), even composite squares, odd squares, odd composite squares, even primes, and odd primes.

Contexts and concepts

A (formal) context consists of a set of objects O, a set of attributes A, and an indication of which objects have which attributes. Formally it can be regarded as a bipartite graph I ⊆ O × A.

	composite	even	odd	prime	square
1			√		√
2		√		√
3			√	√
4	√	√			√
5			√	√
6	√	√
7			√	√
8	√	√
9	√		√		√
10	√	√

A (formal) concept for a context is defined to be a pair (O_i, A_i) such that

1. O_i ⊆ O
2. A_i ⊆ A
3. every object in O_i has every attribute in A_i
4. for every object in O that is not in O_i, there is an attribute in A_i that the object does not have
5. for every attribute in A that is not in A_i, there is an object in O_i that does not have that attribute

O_i is called the extent of the concept, A_i the intent.

A context may be described as a table, with the objects corresponding to the rows of the table, the attributes corresponding to the columns of the table, and a Boolean value (in the example represented graphically as a checkmark) in cell (x, y) whenever object x has value y:

A concept, in this representation, forms a maximal subarray (not necessarily contiguous) such that all cells within the subarray are checked. For instance, the concept highlighted with a different background color in the example table is the one describing the odd prime numbers, and forms a 3 × 2 subarray in which all cells are checked.^[1]

Concept lattice of a context

The concepts (O_i, A_i) defined above can be partially ordered by inclusion: if (O_i, A_i) and (O_j, A_j) are concepts, we define a partial order ≤ by saying that (O_i, A_i) ≤ (O_j, A_j) whenever O_i ⊆ O_j. Equivalently, (O_i, A_i) ≤ (O_j, A_j) whenever A_j ⊆ A_i.

Every pair of concepts in this partial order has a unique greatest lower bound (meet). The greatest lower bound of (O_i, A_i) and (O_j, A_j) is the concept with objects O_i ∩ O_j; it has as its attributes the union of A_i, A_j, and any additional attributes held by all objects in O_i ∩ O_j. Symmetrically, every pair of concepts in this partial order has a unique least upper bound (join). The least upper bound of (O_i, A_i) and (O_j, A_j) is the concept with attributes A_i ∩ A_j; it has as its objects the union of O_i, O_j, and any additional objects that have all attributes in A_i ∩ A_j.

These meet and join operations satisfy the axioms defining a lattice. In fact, by considering infinite meets and joins, analogously to the binary meets and joins defined above, one sees that this is a complete lattice. It may be viewed as the Dedekind–MacNeille completion of a partially ordered set of height two in which the elements of the partial order are the objects and attributes of A and in which two elements x and y satisfy x ≤ y exactly when x is an object that has attribute y.

Any finite lattice may be generated as the concept lattice for some context. For, let L be a finite lattice, and form a context in which the objects and the attributes both correspond to elements of L. In this context, let object x have attribute y exactly when x and y are ordered as x ≤ y in the lattice. Then, the concept lattice of this context is isomorphic to L itself.^[2] This construction may be interpreted as forming the Dedekind–MacNeille completion of L, which is known to produce an isomorphic lattice from any finite lattice.

Concept algebra of a context

Modelling negation in a formal context is somewhat problematic because the complement (O\O_i, A\A_i) of a concept (O_i, A_i) is in general not a concept. However, since the concept lattice is complete one can consider the join (O_i, A_i)^Δ of all concepts (O_j, A_j) that satisfy O_j ⊆ G\O_i; or dually the meet (O_i, A_i)