- Orbital perturbation analysis (spacecraft)
-
Isaac Newton in his Philosophiæ Naturalis Principia Mathematica demonstrated that the gravitational force between two mass points is inversely proportional to the square of the distance between the points and fully solved corresponding "two-body problem" demonstrating that radius vector between the two points would describe an ellipse. But already for the three body problem no exact closed form analytical form could be found. Instead approximate methods were developed, this is the method of "Orbital perturbation analysis". With this technique a quite accurate mathematical description of the trajectories of all the planets could be obtained. Especially critical was the mathematical modeling of the orbit of the Moon as the deviations from a pure Kepler orbit around the Earth due to the gravitational force of the Sun (i.e. one has indeed the three body problem) are much larger than deviations of the orbits of the planets from Sun-centered Kepler orbits caused by the gravitational attraction between the planets. With the availability of digital computers and the easiness to propagate orbits with numerical methods this problem partly disappeared, the motion of all celestial bodies including planets, satellites, asteroids and comets can be modeled and predicted with almost perfect accuracy using the method of the numerical propagation of the trajectories. Never-the-less several analytical closed form expressions for the effect of such additional "perturbing forces" are still very useful
Contents
Orbital perturbation of spacecraft orbits
All celestial bodies of the Solar System follow in first approximation a Kepler orbit around a central body. For a satellite (artificial or natural) this central body is a planet. But both due to gravitational forces caused by the Sun and other celestial bodies and due to the flattening of its planet (caused by its rotation which makes the planet slightly oblate and therefore the result of the Shell theorem not fully applicable) the satellite will follow an orbit that deviates more from a pure Kepler orbit then what is the case for the planets.
The precise modeling of the motion of the Moon has because of this been a difficult task. The best and most accurate modeling for the Moon orbit before the availability of digital computers was obtained with the complicated Delunay and Brown's lunar theories.
But the most important of these perturbation effects, the precession of the orbital plane caused by the slightly oblate shape of the Earth, was already fully understood by Isaac Newton who estimated the oblateness of the Earth from the observed rate of precession of the orbital plane of the Moon.
For man-made spacecraft orbiting the Earth at comparatively low altitudes the deviations from a Kepler orbit are much larger than for the Moon. The approximation of the gravitational force of the Earth to be that of a homogeneous sphere gets worse the closer one gets to the Earth surface and the majority of the artificial Earth satellites are in orbits that are only a few hundred kilometers over the Earth surface. Further more they are (as opposed to the Moon) significantly affected by the solar radiation pressure because of their large cross-section to mass ratio, this applies in particular to 3-axis stabilized spacecraft with large solar arrays. In addition they are significantly affected by rarefied air unless above 800–1000 km (The air drag at high altitudes strongly depending on the solar activity!)
Mathematical approach
Consider any function
of the position
and the velocity
From the chain rule of differentiation one gets that the time derivative of g is
where
 are the components of the force per unit mass acting on the body.
are the components of the force per unit mass acting on the body.If now g is a "constant of motion" for a Kepler orbit like for example an orbital element and the force is corresponding "Kepler force"
one has that
 .
.If the force is the sum of the "Kepler force" and an additional force (force per unit mass)
i.e.
one therefore has
and that the change of
 in the time from
in the time from  to
to  is
isIf now the additional force
 is sufficiently small that the motion will be close to that of a Kepler orbit one gets an approximate value for
is sufficiently small that the motion will be close to that of a Kepler orbit one gets an approximate value for  by evaluating this integral assuming
by evaluating this integral assuming  to precisely follow this Kepler orbit.
to precisely follow this Kepler orbit.In general one wants to find an approximate expression for the change
 over one orbital revolution using the true anomaly
over one orbital revolution using the true anomaly  as integration variable, i.e. as
as integration variable, i.e. as
(
This integral is evaluated setting
 , the elliptical Kepler orbit in polar angles. For the transformation of integration variable from time to true anomaly it was used that the angular momentum
, the elliptical Kepler orbit in polar angles. For the transformation of integration variable from time to true anomaly it was used that the angular momentum  by definition of the parameter
by definition of the parameter  for a Kepler orbit (see equation (13) of the Kepler orbit article).
for a Kepler orbit (see equation (13) of the Kepler orbit article).For the very important case that the Kepler orbit is circular or almost circular
 and (1) takes the simpler form
and (1) takes the simpler form

(
where
 is the orbital period
is the orbital periodPerturbation of the semi-major axis/orbital period
For an elliptic Kepler orbit the sum of the kinetic and the potential energy
where
 is the orbital velocity
is the orbital velocityis a constant and equal to
 (Equation (44) of the Kepler orbit article)
(Equation (44) of the Kepler orbit article)
If
 is the perturbing force and
is the perturbing force and  is the velocity vector of the Kepler orbit the equation (1) takes the form:
is the velocity vector of the Kepler orbit the equation (1) takes the form:
(
and for a circular or almost circular orbit

(
From the change
 of the parameter
of the parameter  the new semi-major axis
the new semi-major axis  and the new period
and the new period  are computed (relations (43) and (44) of the Kepler orbit article).
are computed (relations (43) and (44) of the Kepler orbit article).Perturbation of the orbital plane
Let
 and
and  make up a rectangular coordinate system in the plane of the reference Kepler orbit. If
make up a rectangular coordinate system in the plane of the reference Kepler orbit. If  is the argument of perigee relative the
is the argument of perigee relative the  and
and  coordinate system the true anomaly
coordinate system the true anomaly  is given by
is given by  and the approximate change
and the approximate change  of the orbital pole
of the orbital pole  (defined as the unit vector in the direction of the angular momentum) is
(defined as the unit vector in the direction of the angular momentum) is![\Delta \hat{z}\ =\ \int\limits_{0}^{2\pi}\frac{f_z }{V_t} (\hat{g} \cos u + \hat{h} \sin u)\frac{r^2}{\sqrt{\mu p}}du \quad \times \ \hat{z}
=\ \frac{1}{\mu p}\left[\hat{g}\int\limits_{0}^{2\pi}f_z r^3 \cos u \ du
+\ \hat{h}\int\limits_{0}^{2\pi}f_z r^3 \sin u \ du \right]\quad \times \ \hat{z}](e/94e34ec4f89a7fc445a20bd4dae685a5.png)
(
where
 is the component of the perturbing force in the
is the component of the perturbing force in the  direction,
direction,  is the velocity component of the Kepler orbit orthogonal to radius vector and
is the velocity component of the Kepler orbit orthogonal to radius vector and  is the distance to the center of the Earth.
is the distance to the center of the Earth.For a circular or almost circular orbit (5) simplifies to
![\Delta \hat{z}\ =\ \frac{r^2}{\mu}\left[\hat{g}\int\limits_{0}^{2\pi}f_z \cos u \ du
+\ \hat{h}\int\limits_{0}^{2\pi}f_z \sin u \ du \right]\quad \times \ \hat{z}](c/e3c422ec3713edbeb48297347ccd9810.png)
(
Example
In a circular orbit a low-force propulsion system (Ion thruster) generates a thrust (force per unit mass) of
 in the direction of the orbital pole in the half of the orbit for which
in the direction of the orbital pole in the half of the orbit for which  is positive and in the opposite direction in the other half. The resulting change of orbit pole after one orbital revolution of duration
is positive and in the opposite direction in the other half. The resulting change of orbit pole after one orbital revolution of duration  is
is![\Delta \hat{z}\ =\ \frac{r^2}{\mu}\left[\ 2\ F\int\limits_{0}^{\pi}\sin u \ du \right]\quad \hat{h}\times \hat{z} =
\ \frac{r^2}{\mu}\ 4\ F\ \quad \hat{g}](0/57022c01384a7de9093657eb86a13f8e.png)
(
The average change rate
 is therefore
is therefore
(
where
 is the orbital velocity in the circular Kepler orbit.
is the orbital velocity in the circular Kepler orbit.Perturbation of the eccentricity vector
Rather than applying (1) and (2) on the partial derivatives of the orbital elements eccentricity and argument of perigee directly one should apply these relations for the eccentricity vector. First of all the typical application is a near-circular orbit. But there are also mathematical advantages working with the partial derivatives of the components of this vector also for orbits with a significant eccentricity.
Equations (60), (55) and (52) of the Kepler orbit article say that the eccentricity vector is

(
where

(

(
from which follows that

(

(
where

(

(
(Equations (18) and (19) of the Kepler orbit article)
The eccentricity vector is by definition always in the osculating orbital plane spanned by
 and
and  and formally there is also a derivative
and formally there is also a derivativewith
corresponding to the rotation of the orbital plane
But in practice the in-plane change of the eccentricity vector is computed as

(
ignoring the out-of-plane force and the new eccentricity vector
is subsequently projected to the new orbital plane orthogonal to the new orbit normal
computed as described above.
Example
The Sun is in the orbital plane of a spacecraft in a circular orbit with radius
 and consequently with a constant orbital velocity
and consequently with a constant orbital velocity  . If
. If  and
and  make up a rectangular coordinate system in the orbital plane such that
make up a rectangular coordinate system in the orbital plane such that  points to the Sun and assuming that the solar radiation pressure force per unit mass
points to the Sun and assuming that the solar radiation pressure force per unit mass  is constant one gets that
is constant one gets thatwhere
 is the polar angle of
is the polar angle of  in the
in the  ,
,  system. Applying (2) one gets that
system. Applying (2) one gets that
(
This means the eccentricity vector will gradually increase in the direction
 orthogonal to the Sun direction. This is true for any orbit with a small eccentricity, the direction of the small eccentricity vector does not matter. As
orthogonal to the Sun direction. This is true for any orbit with a small eccentricity, the direction of the small eccentricity vector does not matter. As  is the orbital period this means that the average rate of this increase will be
is the orbital period this means that the average rate of this increase will be 
The effect of the Earth flattening
In the article Geopotential model the modeling of the gravitational field as a sum of spherical harmonics is discussed. The by far dominating term is the "J2-term". This is a "zonal term" and corresponding force is therefore completely in a longitudinal plane with one component
 in the radial direction and one component
in the radial direction and one component  with the unit vector
with the unit vector  orthogonal to the radial direction towards north. These directions
orthogonal to the radial direction towards north. These directions  and
and  are illustrated in Figure 1.
are illustrated in Figure 1.To be able to apply relations derived in the previous section the force component
 must be split into two orthogonal components
must be split into two orthogonal components  and
and  as illustrated in figure 2
as illustrated in figure 2Let
 make up a rectangular coordinate system with origin in the center of the Earth (in the center of the Reference ellipsoid) such that
make up a rectangular coordinate system with origin in the center of the Earth (in the center of the Reference ellipsoid) such that  points in the direction north and such that
points in the direction north and such that  are in the equatorial plane of the Earth with
are in the equatorial plane of the Earth with  pointing towards the ascending node, i.e. towards the blue point of Figure 2.
pointing towards the ascending node, i.e. towards the blue point of Figure 2.The components of the unit vectors
making up the local coordinate system (of which
 are illustrated in figure 2) relative the
are illustrated in figure 2) relative the  are
arewhere
 is the polar argument of
is the polar argument of  relative the orthogonal unit vectors
relative the orthogonal unit vectors  and
and  in the orbital plane
in the orbital planeFirstly
where
 is the angle between the equator plane and
is the angle between the equator plane and  (between the green points of figure 2) and from equation (12) of the article Geopotential model one therefore gets that
(between the green points of figure 2) and from equation (12) of the article Geopotential model one therefore gets that
(
Secondly the projection of direction north,
 , on the plane spanned by
, on the plane spanned by  is
isand this projection is
where
 is the unit vector
is the unit vector  orthogonal to the radial direction towards north illustrated in figure 1.
orthogonal to the radial direction towards north illustrated in figure 1.From equation (12) of the article Geopotential model one therefore gets that
and therefore:

(

(
Perturbation of the orbital plane
From (5) and (20) one gets that
![\Delta \hat{z}\ =\ -J_2\ \frac{3\ \sin i\ \cos i}{\mu p^2}\left[\hat{g}\int\limits_{0}^{2\pi}\frac{p}{r}\ \sin u\ \cos u \ du
+\ \hat{h}\int\limits_{0}^{2\pi}\frac{p}{r}\ \sin^2 u\ du \right]\quad \times \ \hat{z}](d/fdd3f30f823487037f2351b0ea2fc6d5.png)
(
The fraction
 is
iswhere
 is the eccentricity and
is the eccentricity and  is the argument of perigee of the reference Kepler orbit
is the argument of perigee of the reference Kepler orbitAs all integrals of type
are zero if not both
 and
and  are even one gets from (21) that
are even one gets from (21) thatAs
this can be written

(
As
 is an inertially fixed vector (the direction of the spin axis of the Earth) relation (22) is the equation of motion for a unit vector
is an inertially fixed vector (the direction of the spin axis of the Earth) relation (22) is the equation of motion for a unit vector  describing a cone around
describing a cone around  with a precession rate (radians per orbit) of
with a precession rate (radians per orbit) of 
In terms of orbital elements this is expressed as

(

(
where
 is the inclination of the orbit to the equatorial plane of the Earth
is the inclination of the orbit to the equatorial plane of the Earth
 is the right ascension of the ascending node
is the right ascension of the ascending node
Perturbation of the eccentricity vector
From (16), (18) and (19) follows that in-plane perturbation of the eccentricity vector is

(
the new eccentricity vector being the projection of
on the new orbital plane orthogonal to
where
 is given by (22)
is given by (22)Relative the coordinate system
one has that
Using that
and that
where
are the components of the eccentricity vector in the
 coordinate system this integral (25) can be evaluated analytically, the result is
coordinate system this integral (25) can be evaluated analytically, the result is
(
This the difference equation of motion for the eccentricity vector
 to form a circle, the magnitude of the eccentricity
to form a circle, the magnitude of the eccentricity  staying constant.
staying constant.Translating this to orbital elements it must be remembered that the new eccentricity vector obtained by adding
 to the old
to the old  must be projected to the new orbital plane obtained by applying (23) and (24)
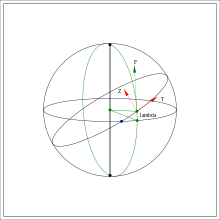
must be projected to the new orbital plane obtained by applying (23) and (24)This is illustrated in figure 3:
To the change in argument of the eccentricity vector
must be added an increment due to the precession of the orbital plane (caused by the out-of-plane force component) amounting to
One therefore gets that

(

(
In terms of the components of the eccentricity vector
 relative the coordinate system
relative the coordinate system  that precesses around the polar axis of the Earth the same is expressed as follows
that precesses around the polar axis of the Earth the same is expressed as follows
(
where the first term is the in-plane perturbation of the eccentricity vector and the second is the effect of the new position of the ascending node in the new plane
From (28) follows that is zero if
is zero if  . This fact is used for Molniya orbits having an inclination of 63.4 deg. An orbit with an inclination of 180 - 63.4 deg = 116.6 deg would in the same way have a constant argument of perigee.
. This fact is used for Molniya orbits having an inclination of 63.4 deg. An orbit with an inclination of 180 - 63.4 deg = 116.6 deg would in the same way have a constant argument of perigee.Proof
Proof that the integral

(
where:
has the value

(
Integrating the first term of the integrand one gets:

(
and

(
For the second term one gets:

(
and

(
For the third term one gets:

(
and

(
For the fourth term one gets:

(
and

(
Adding the right hand sides of (32), (34), (36) and (38) one gets

Adding the right hand sides of (33), (35), (37) and (39) one gets

References
- El'Yasberg "Theory of flight of artificial earth satellites", Israel program for Scientific Translations (1967)
See also
- Frozen orbit
- Molniya orbit
Categories:
Wikimedia Foundation. 2010.





















 orthogonal to
orthogonal to 
























 caused by the in-plane force components and a contribution
caused by the in-plane force components and a contribution  caused by the use of the ascending node as reference
caused by the use of the ascending node as reference




