Mollweide's formula

Figure 1 – A triangle. The angles α, β, and γ are respectively opposite the sides a, b, and c.

Trigonometry
History Usage Functions Generalized Inverse functions Further reading
Reference
Identities Exact constants Trigonometric tables
Laws and theorems
Law of sines Law of cosines Law of tangents Law of cotangents Pythagorean theorem
Calculus
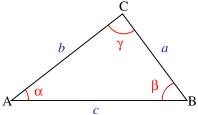
Trigonometric substitution Integrals of functions Derivatives of functions Integrals of inverse functions
v · d · e

In trigonometry, Mollweide's formula, sometimes referred to in older texts as Mollweide's equations,^[1] named after Karl Mollweide, is a set of two relationships between sides and angles in a triangle.^[2] It can be used to check solutions of triangles.^[3]

Let a, b, and c be the lengths of the three sides of a triangle. Let α, β, and γ be the measures of the angles opposite those three sides respectively. Mollweide's formula states that

$\frac{a + b}{c} = \frac{\cos\left(\frac{\alpha - \beta}{2}\right)}{\sin\left(\frac{\gamma}{2}\right)}$

and

$\frac{a - b}{c} = \frac{\sin\left(\frac{\alpha - \beta}{2}\right)}{\cos\left(\frac{\gamma}{2}\right)}.$

Each of these identities uses all six parts of the triangle—the three angles and the lengths of the three sides.

See also

• Law of sines
• Law of cosines
• Law of tangents
• Law of cotangents

Notes

1. ^ Ernest Julius Wilczynski, Plane Trigonometry and Applications, Allyn and Bacon, 1914, page 102
2. ^ Michael Sullivan, Trigonometry, Dellen Publishing Company, 1988, page 243.
3. ^ Ernest Julius Wilczynski, Plane Trigonometry and Applications, Allyn and Bacon, 1914, page 105

References

• H. Arthur De Kleine, "Proof Without Words: Mollweide's Equation", Mathematics Magazine, volume 61, number 5, page 281, December, 1988.