M-sigma relation

The M-sigma (or M_BH-σ) relation is an empirical correlation between the stellar velocity dispersion σ of a galaxy bulge and the mass M of the supermassive black hole at the galaxy's center.

The relation can be expressed mathematically as

$M \propto \sigma^\alpha .$

A recent study, based on a complete sample of published black hole masses in nearby galaxies, ^[1] gives

$\log(M/M_\odot) = 8.12\pm0.08~+~(4.24\pm0.41)\log(\sigma/200~{\rm km}~{\rm }s^{-1}).$

The scatter about the mean relation is comparable to that of other empirical relations between black hole mass and galaxy properties.^[1] The small scatter is generally interpreted to imply some source of mechanical feedback between the growth of supermassive black holes and the growth of galaxy bulges, although the source of this feedback is still uncertain.

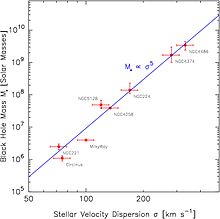Black hole mass plotted against velocity dispersion of stars in the galaxy bulge. Points are labelled by galaxy name; all points in this diagram are for galaxies which exhibit a clear, Keplerian rise in velocity near the center, indicative of the presence of a central mass. The M − σ relation is shown in blue.

The M − σ relation was discovered in 2000 ^{[2] [3]} by two independent groups. Earlier work had demonstrated a possible relationship between galaxy luminosity and black hole mass^[4], but that relationship had larger scatter and did not motivate the conclusion that all luminous galaxies are likely to have black holes. Discovery of the M − σ relation produced a sea change in research on black holes in the nuclei of galaxies. Prior to that time the main concern had been the simple detection of black holes, while afterward the interest changed to understanding the role of supermassive black holes as a critical component of galaxies. This led to the main uses of the relation to estimate black hole masses in galaxies that are too distant for direct mass measurements to be made, and to assay the overall black hole content of the Universe.

Origin

The tightness of the M − σ relation suggests that some kind of feedback acts to maintain the connection between black hole mass and stellar velocity dispersion, in spite of processes like galaxy mergers and gas accretion that might be expected to increase the scatter over time. One such mechanism was suggested by Joseph Silk and Martin Rees in 1998 ^[5]. These authors proposed a model in which supermassive black holes first form via collapse of giant gas clouds before most of the bulge mass has turned into stars. The black holes created in this way would then accrete and radiate, driving a wind which acts back on the accretion flow. The flow would stall if the rate of deposition of mechanical energy into the infalling gas was large enough to unbind the protogalaxy in one crossing time. The Silk and Rees model predicts a slope for the M − σ relation of α = 5, which is somewhat larger than observed, but does predict approximately the correct normalization of the relation.

Importance

Before the M − σ relation was discovered in 2000, a large discrepancy existed between black hole masses derived using three techniques.^[6] Direct, or dynamical, measurements based on the motion of stars or gas near the black hole seemed to give masses that averaged ~1% of the bulge mass (the "Magorrian relation"). Two other techniques -- reverberation mapping in active galactic nuclei, and the Soltan argument, which computes the cosmological density in black holes needed to explain the quasar light -- both gave a mean value of M/M_bulge that was a factor ~10 smaller than implied by the Magorrian relation. The M − σ relation resolved this discrepancy by showing that most of the direct black hole masses published prior to 2000 were significantly in error, presumably because the data on which they were based were of insufficient quality to resolve the black hole's dynamical sphere of influence. The mean ratio of black hole mass to bulge mass is now believed to be approximately 0.1% ^[7], i.e., a bulge of one billion solar masses contains a black hole of approximately one million solar masses.

A common use of the M − σ relation is to estimate black hole masses in distant galaxies using the easily-measured quantity σ. Black hole masses in thousands of galaxies have been estimated in this way. The M − σ relation is also used to calibrate so-called secondary and tertiary mass estimators, which relate the black hole mass to the strength of emission lines from hot gas in the nucleus or to the velocity dispersion of gas in the bulge ^[8].

The tightness of the M − σ relation has led to suggestions that every bulge must contain a supermassive black hole. However, the number of galaxies in which the effect of the black hole's gravity on the motion of stars or gas is unambiguously seen is still quite small^[9]. It is unclear whether the lack of black hole detections in many galaxies implies that these galaxies do not contain black holes; or that their masses are significantly below the value implied by the M − σ relation; or that the data are simply too poor to reveal the presence of the black hole ^[10].

The smallest supermassive black hole with a well-determined mass has M≈10⁶ solar masses (see figure). The existence of black holes in the mass range 10⁴ − 10⁶ solar masses ("intermediate-mass black holes") is predicted by the M − σ relation in low-mass galaxies, and the existence of intermediate mass black holes has been reasonably well established in a number of galaxies which contain active galactic nuclei, although the values of M in these galaxies are highly uncertain ^[11]. No clear evidence has been found for ultra-massive black holes with masses above 10¹⁰ solar masses, although this may be an expected consequence of the observed upper limit to σ ^[12].

See also

• Faber-Jackson relation

References

1. ^ ^{a b} Gultekin, K. et al. (2009), The M − σ and M-L Relations in Galactic Bulges, and Determinations of Their Intrinsic Scatter, Astrophysical Journal, 698, 198-221
2. ^ Ferrarese, F. and Merritt, D. (2000), A Fundamental Relation between Supermassive Black Holes and Their Host Galaxies, The Astrophysical Journal, 539, L9-L12
3. ^ Gebhardt, K. et al. (2000), A Relationship between Nuclear Black Hole Mass and Galaxy Velocity Dispersion, The Astrophysical Journal, 539, L13-L16
4. ^ Magorrian, J. et al. (1998), The Demography of Massive Dark Objects in Galaxy Centers, The Astronomical Journal, 115, 2285-2305
5. ^ Silk, J. and Rees, M. (1998), Quasars and galaxy formation, Astronomy and Astrophysics, 331, L1-L4
6. ^ Merritt, D. and Ferrarese, L. (2001), Relationship of Black Holes to Bulges [1]
7. ^ Merritt, D. and Ferrarese, L. (2001), Black hole demographics from the M − σ relation, Monthly Notices of the Royal Astronomical Society, 320, L30-L34
8. ^ Peterson, B. (2008), The central black hole and relationships with the host galaxy, New Astronomy Reviews, 52, 240-252
9. ^ Batcheldor, D. (2010), "The M-σ Relation Derived from Sphere of Influence Arguments", The Astrophysical Journal 711: L108-L112, Bibcode 2010ApJ...711L.108B, doi:10.1088/2041-8205/711/2/L108, http://adsabs.harvard.edu/abs/2010ApJ...711L.108B 
10. ^ Valluri, M. et al. (2004), Difficulties with Recovering the Masses of Supermassive Black Holes from Stellar Kinematical Data, The Astrophysical Journal, 602, 66-92
11. ^ Ho, L. (2008), Nuclear activity in nearby galaxies, Annual Review of Astronomy & Astrophysics, 46, 475-539
12. ^ Batcheldor, D. et al. (2007), How Special Are Brightest Cluster Galaxies?, The Astrophysical Journal, 663, L85-L88