Population dynamics of fisheries

A fishery is an area with an associated fish or aquatic population which is harvested for its commercial or recreational value. Fisheries can be wild or farmed. Population dynamics describes the ways in which a given population grows and shrinks over time, as controlled by birth, death, and emigration or immigration. It is the basis for understanding changing fishery patterns and issues such as habitat destruction, predation and optimal harvesting rates. The population dynamics of fisheries is used by fisheries scientists to determine sustainable yields. [Wilderbuera, Thomas K and Zhang, Chang Ik (1999) [http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6T6N-3WDKGMG-7&_user=10&_rdoc=1&_fmt=&_orig=search&_sort=d&view=c&_acct=C000050221&_version=1&_urlVersion=0&_userid=10&md5=a9c222a53c510d31b89d6ece311422be "Evaluation of the population dynamics and yield characteristics of Alaska plaice, Pleuronectes quadrituberculatus, in the eastern Bering Sea."] Fisheries Research.Volume 41, Issue 2.] [Richard W Zabel, Chris J Harvey, Steven L Katz, Thomas P Good, Phillip S Levin (2003) [http://www.americanscientist.org/template/AssetDetail/assetid/17216/page/8?&print=yes "Ecologically Sustainable Yield."] American Scientist, March–April.] [ [http://en.wikipedia.org/w/index.php?title=Population_dynamics_of_fisheries&action=edit A Sustainable Fishing Simulation Using Mathematical Modeling] ]

The basic accounting relation for population dynamics is:

: "N"₁ = "N"₀ + "B" − "D" + "I" − "E"

where "N"₁ is the number of individuals at time 1, "N"₀ is the number of individuals at time 0, "B" is the number of individuals born, "D" the number that died, "I" the number that immigrated, and "E" the number that emigrated between time 0 and time 1. While immigration and emigration can be present in wild fisheries, they are usually not measured.

A fishery population is affected by three dynamic rate functions:

* Birth rate or recruitment. Recruitment means reaching a certain size or reproductive stage. With fisheries, recruitment usually refers to the age a fish can be caught and counted in nets.

*Growth rate. This measures the growth of individuals in size and length. This is important in fisheries where the population is often measured in terms of biomass.
*Mortality. This includes harvest mortality and natural mortality. Natural mortality includes non-human predation, disease and old age.

If these rates are measured over different time intervals, the harvestable surplus of a fishery can be determined. The harvestable surplus is the number of individuals that can be harvested from the population without affecting long term stability (average population size). The harvest within the harvestable surplus is called compensatory mortality, where the harvest deaths are substituting for the deaths that would otherwise occur naturally. Harvest beyond that is additive mortality, harvest in addition to all the animals that would have died naturally.

History

The first principle of population dynamics is widely regarded as the exponential law of Malthus, as modelled by the Malthusian growth model. The early period was dominated by demographic studies such as the work of Benjamin Gompertz and Pierre François Verhulst in the early 19th century, who refined and adjusted the Malthusian demographic model. A more general model formulation was proposed by F.J. Richards in 1959, by which the models of Gompertz, Verhulst and also Ludwig von Bertalanffy are covered as special cases of the general formulation.

Population size

The population size (usually denoted by "N") is the number of individual organisms in a population.

The effective population size ("N"_"e") was defined by Sewall Wright, who wrote two landmark papers on it (Wright 1931, 1938). He defined it as "the number of breeding individuals in an idealized population that would show the same amount of dispersion of allele frequencies under random genetic drift or the same amount of inbreeding as the population under consideration". It is a basic parameter in many models in population genetics. "N"_"e" is usually less than "N" (the absolute population size).

Small population size results in increased genetic drift. Population bottlenecks are when population size reduces for a short period of time.

Overpopulation may indicate any case in which the population of any species of animal may exceed the carrying capacity of its ecological niche.

Virtual population analysis

Virtual population analysis (VPA) is a modelling technique commonly used in fisheries science for reconstructing historical fish numbers using information on death of individuals each year. This death is usually partitioned into catch by fisheries and natural mortality.

VPA is the most commonly used term to refer to cohort reconstruction techniques used in fisheries. It is virtual in the sense that the population size is not observed or measured directly but is inferred or back-calculated to have been a certain size in the past in order to support the observed fish catches and an assumed death rate owing to non-fishery related causes.

Minimum viable population

The minimum viable population (MVP) is a lower bound on the population of a species, such that it can survive in the wild. More specifically MVP is the smallest possible size at which a biological population can exist without facing extinction from natural disasters or demographic, environmental, or genetic stochasticity. [Holsinger (2007)] The term "population" refers to the population of a species in the wild.

As a reference standard, MVP is usually given with a population survival probability of somewhere between ninety and ninety-five percent and calculated for between one hundred and one thousand years into the future.

The MVP can be calculated using computer simulations known as population viability analyses (PVA), where populations are modelled and future population dynamics are projected.

Maximum sustainable yield

In population ecology and economics, maximum sustainable yield or MSY is, theoretically, the largest catch that can be taken from a fishery stock over an indefinite period. [Europa: European Union (2006) [http://europa.eu/scadplus/leg/en/lvb/l66037.htm Management based on maximum sustainable yield] ] [Europa: European Union (2006) [http://europa.eu/rapid/pressReleasesAction.do?reference=MEMO/06/268&format=HTML&aged=0&language=EN&guiLanguage=en Questions and Answers on Maximum Sustainable Yield (MSY)] ] Under the assumption of logistic growth, the MSY will be exactly at half the carrying capacity of a species, as this is the stage at when population growth is highest. The maximum sustainable yield is usually higher than the optimum sustainable yield.

This logistic model of growth is produced by a population introduced to a new habitat or with very poor numbers going through a lag phase of slow growth at first. Once it reaches a foothold population it will go through a rapid growth rate that will start to level off once the species approaches carrying capacity. The idea of maximum sustained yield is to decrease population density to the point of highest growth rate possible. This changes the number of the population, but the new number can be maintained indefinitely, ideally.

MSY is extensively used for fisheries management. [WWF Publications (2007) [http://www.panda.org/about_wwf/where_we_work/europe/what_we_do/epo/initiatives/fisheries/publications/index.cfm?uNewsID=97580 "The Maximum Sustainable Yield objective in Fisheries"] ] [New Zealand Ministry of Fisheries. [http://www.fish.govt.nz/en-nz/SOF/Indicators.htm "MSY Harvest Strategies."] ] Unlike the logistic (Schaefer) model, MSY in most modern fisheries models occurs at around 30% of the unexploited population size. This fraction differs among populations depending on the life history of the species and the age-specific selectivity of the fishing method.

Overfishing

[

---

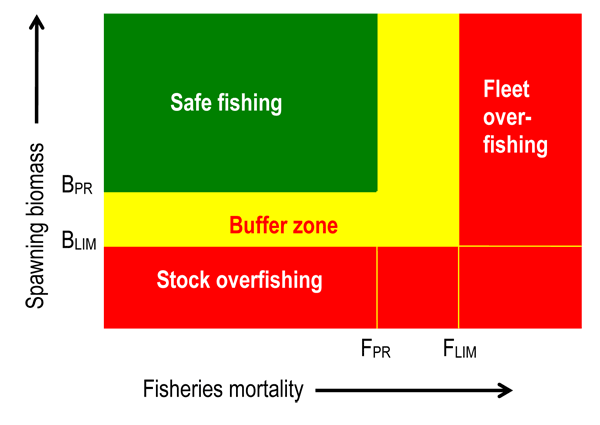
thumb|right|300px|The_Traffic_Light_colour_convention,_showing_the_concept_of_Harvest_Control_Rule_(HCR),_specifying_when_a_rebuilding_plan_is_mandatory_in_terms_of_precautionary and limit reference points for spawning biomass and fishing mortality rate.] The notion of overfishing hinges on what is meant by an acceptable level of fishing.

A current operational model used by some fisheries for predicting acceptable levels is the Harvest Control Rule (HCR). This formalizes and summarizes a management strategy which can actively adapt to subsequent feedback. The HCR is a variable over which the management has some direct control and describes how the harvest is intended to be controlled by management in relation to the state of some indicator of stock status. For example, a harvest control rule can describe the various values of fishing mortality which will be aimed at for various values of the stock abundance. Constant catch and constant fishing mortality are two types of simple harvest control rules. [Coad, Brian W and McAllister, Don E (2008) [http://www.briancoad.com/dictionary/H.htm "Dictionary of Ichthyology."] ]

* Biological overfishing occurs when fishing mortality has reached a level where the stock biomass has negative marginal growth (slowing down biomass growth), as indicated by the red area in the figure. Fish are being taken out of the water so quickly that the replenishment of stock by breeding slows down. If the replenishment continues to slow down for long enough, replenishment will go into reverse and the population will decrease.

* Economic or bioeconomic overfishing additionally considers the cost of fishing and defines overfishing as a situation of negative marginal growth of resource rent. Fish are being taken out of the water so quickly that the growth in the profitability of fishing slows down. If this continues for long enough, profitability will decrease.

Metapopulation

A metapopulation is a group of spatially separated populations of the same species which interact at some level. The term was coined by Richard Levins in 1969. The idea has been most broadly applied to species in naturally or artificially fragmented habitats. In Levins' own words, it consists of "a population of populations". [Levins, R. 1969. "Some demographic and genetic consequences of environmental heterogeneity for biological control." Bulletin of the Entomological Society of America, 15, 237-240]

A metapopulation generally consists of several distinct populations together with areas of suitable habitat which are currently unoccupied. Each population cycles in relative independence of the other populations and eventually goes extinct as a consequence of demographic stochasticity (fluctuations in population size due to random demographic events); the smaller the population, the more prone it is to extinction.

Although individual populations have finite life-spans, the population as a whole is often stable because immigrants from one population (which may, for example, be experiencing a population boom) are likely to re-colonize habitat which has been left open by the extinction of another population. They may also emigrate to a small population and rescue that population from extinction (called the "rescue effect").

Age class structure

Age can be determined by counting growth rings in fish scales, otoliths, cross-sections of fin spines for species with thick spines such as triggerfish, or teeth for a few species. Each method has its merits and drawbacks. Fish scales are easiest to obtain, but may be unreliable if scales have fallen off of the fish and new ones grown in their places. Fin spines may be unreliable for the same reason, and most fish do not have spines of sufficient thickness for clear rings to be visible. Otoliths will have stayed with the fish throughout its life history, but obtaining them requires killing the fish. Also, otoliths often require more preparation before ageing can occur.

An age class structure with gaps in it, for instance a regular bell curve for the population of 1-5 year-old fish, excepting a very low population for the 3-year-olds, implies a bad spawning year 3 years ago in that species.

Often fish in younger age class structures have very low numbers because they were small enough to slip through the sampling nets, and may in fact have a very healthy population.

Population cycle

A population cycle occurs where populations rise and fall over a predictable period of time. There are some species where population numbers have reasonably predictable patterns of change although the full reasons for population cycles is one of the major unsolved ecological problems. There are a number of factors which influence population change such as availability of food, predators, diseases and climate.

Trophic cascades

Trophic cascades occur when predators in a food chain suppress the abundance of their prey, thereby releasing the next lower trophic level from predation (or herbivory if the intermediate trophic level is an herbivore). For example, if the abundance of large piscivorous fish is increased in a lake, the abundance of their prey, zooplanktivorous fish, should decrease, large zooplankton abundance should increase, and phytoplankton biomass should decrease. This theory has stimulated new research in many areas of ecology. Trophic cascades may also be important for understanding the effects of removing top predators from food webs, as humans have done in many places through hunting and fishing activities.

;Classic examples
# In lakes, piscivorous fish can dramatically reduce populations of zooplanktivorous fish, zooplanktivorous fish can dramatically alter freshwater zooplankton communities, and zooplankton grazing can in turn have large impacts on phytoplankton communities. Removal of piscivorous fish can change lake water from clear to green by allowing phytoplankton to flourish [Carpenter SR, Kitchell JF, Hodgson JR (1985) Cascading trophic interactions and lake productivity. Bioscience 35:634-639] .
# In the Eel River, in Northern California, fish (steelhead and roach) consume fish larvae and predatory insects. These smaller predators prey on midge larvae, which feed on algae. Removal of the larger fish increases the abundance of algae [Power ME (1990) Effects of fish in river food webs. Science 250: 811-814] .
# In Pacific kelp forests, sea otters feed on sea urchins. In areas where sea otters have been hunted to extinction, sea urchins increase in abundance and decimate kelp [Estes JA, Palmisano JF (1974) Sea otters: their role in structuring nearshore communities. Science 185: 1058-1060]

A recent theory, the mesopredator release hypothesis, states that the decline of top predators in an ecosystem results in increased populations of medium-sized predators (mesopredators).

Predator-prey equations

The classic predator-prey equations are a pair of first order, non-linear, differential equations used to describe the dynamics of biological systems in which two species interact, one a predator and one its prey. They were proposed independently by Alfred J. Lotka in 1925 and Vito Volterra in 1926.

An extension to these are the competitive Lotka-Volterra equations, which provide a simple model of the population dynamics of species competing for some common resource.

In the 1930s Alexander Nicholson and Victor Bailey developed a model to describe the population dynamics of a coupled predator-prey system. The model assumes that predators search for prey at random, and that both predators and prey are assumed to be distributed in a non-contagious ("clumped") fashion in the environment. [Hopper]

Other models

* The individual growth model, published by von Bertalanffy in 1934, can be used to model the rate at which fish grow. It exists in a number of versions, but in its simplest form it is expressed as a differential equation of length ("L") over time ("t"):

:: $L\text{'}(t)\; =\; r\_B\; left(\; L\_infty\; -\; L(t)\; ight)$

:where "r"_"B" is the von Bertalanffy growth rate and "L"_∞ the ultimate length of the individual.

* The Ricker model is a classic discrete population model which gives the expected number (or density) of individuals "N"_{"t" + 1} in generation "t" + 1 as a function of the number of individuals in the previous generation,

:: $N\_\{t+1\}\; =\; N\_t\; e^\{r(1-frac\{N\_t\}\{k\})\}$

:Here "r" is interpreted as an intrinsic growth rate and "k" as the carrying capacity of the environment. The Ricker model was introduced in the context of the fisheries by Ricker (1954).

* Nurgaliev's law says

:: $\{dN\; over\; dt\}\; =\; aN^2\; -\; bN$

:where "N" is the size of a population, "a" is a half of the average probability of a birth of a male (the same for females) of a potential arbitrary parents pair within a year, and "b" is an average probability of a death of a fish within a year.

ee also

* Wild fisheries
* Overfishing
* Beverton–Holt model
* Verhulst
* Schaefer short-term catch equation
* Tragedy of the commons

Notes

References

* Berryman, Alan (2002) "Population Cycles." Oxford University Press US. ISBN 0-19-514098-2
* Brännström A and Sumpter DJ (2005) The role of competition and clustering in population dynamics. Proc Biol Sci. Oct 7 272(1576):2065-72 [1]
* Geritz SA and Kisdi E (2004). On the mechanistic underpinning of discrete-time population models with complex dynamics. J Theor Biol. 2004 May 21;228(2):261-9.
* Hopper, J L (1987) "Opportunities and Handicaps of Antipodean Scientists: A. J. Nicholson and V. A. Bailey on the Balance of Animal Populations," "Historical Records of Australian Science" 7(2), pp. 179–188. [http://www.publish.csiro.au/paper/HR9880720179.htm]
* Kazan-Zelenodolsk; "'Law' of Two Hundred Billions in Context of Civil Society". In materials of Inter-regional scientific-practical conference "The Civil Society: Ideas, Reality, Prospects", on April 27, 2006, , p. 204-207. ISBN 5-8399-0153-9.
* Ricker, WE (1954). Stock and recruitment. Journal of the Fisheries Research Board of Canada.
* Sparre, Per and Hart, Paul J B (2002) Handbook of Fish Biology and Fisheries, [http://en.wikipedia.org/w/index.php?title=Fisheries_science&action=edit Chapter13: "Choosing the best model for fisheries assessment."] Blackwell Publishing. ISBN 063206482X
* Turchin, P. 2003. Complex Population Dynamics: a Theoretical/Empirical Synthesis. Princeton, NJ: Princeton University Press.
* Wright, S. (1931). Evolution in Mendelian populations. "Genetics" 16: 97-159 [http://www.esp.org/foundations/genetics/classical/holdings/w/sw-31.pdf Offsite pdf file]
* Wright, S. (1938). Size of population and breeding structure in relation to evolution. "Science" 87:430-431
* (2007): [http://darwin.eeb.uconn.edu/eeb310/lecture-notes/small-populations/node4.html Types of stochastic threats] . Version of 2007-SEP-04. Retrieved 2007-NOV-04.
* "Encyclopædia Britannica Online" 25 August 2005 "Population Ecology" article section on Population Cycles

Futher reading

* de Vries, Gerda; Hillen, Thomas; Lewis, Mark; Schonfisch, Birgitt and Muller, Johannes (2006) [http://books.google.co.nz/books?id=Vz1pL7FxHN8C&pg=PA212&lpg=PA212&dq=%22Ricker+model%22&source=web&ots=CNxKPbRDK3&sig=AyuPP5aBQyBbtct7efNoH3nwvsA&hl=en&sa=X&oi=book_result&resnum=18&ct=result "A Course in Mathematical Biology"] SIAM. ISBN 9780898716122
* Haddon, Malcolm (2001) [http://books.google.co.nz/books?id=TP_6Z4ukIZQC&pg=PA247&lpg=PA247&dq=recruitment+fisheries%7Cfishery&source=web&ots=N4V8aFhfNm&sig=1bAXBNJf8fGNBrRohmbD6F6p62g&hl=en&sa=X&oi=book_result&resnum=13&ct=result "Modelling and quantitative methods in fisheries"] Chapman & Hall. ISBN 9781584881773
* Hilborn, Ray and Walters, Carl J (1992) [http://books.google.co.nz/books?id=WJg0OVEQHcQC&pg=RA3-PA278&lpg=RA3-PA278&dq=%22Ricker+model%22&source=web&ots=eG4qRqCk8p&sig=FFS-fvP3oua0j3nOTvUyCzR-3Qg&hl=en&sa=X&oi=book_result&resnum=40&ct=result "Quantitative Fisheries Stock Assessment"] Springer. ISBN 9780412022715
* McCallum, Hamish (2000) [http://books.google.co.nz/books?id=r9KnI2kkQ30C&pg=PA175&lpg=PA175&dq=%22Ricker+model%22&source=web&ots=F4hGTL-f-v&sig=jTBqwbY-TRcWHJZnHm97ipeP4Ww&hl=en&sa=X&oi=book_result&resnum=43&ct=result "Population Parameters"] Blackwell Publishing. ISBN 9780865427402
* Turchin, Peter (2003) [http://books.google.co.nz/books?id=GwwkjhlmM8AC&pg=PA54&lpg=PA54&dq=%22Ricker+model%22&source=web&ots=gpqpPz4C60&sig=gSZlCkNcsW55e0wuTjqFvmYSFVA&hl=en&sa=X&oi=book_result&resnum=20&ct=result "Complex Population Dynamics"] Princeton University Press. ISBN 9780691090214