- Conversion between quaternions and Euler angles
-
Spatial rotations in three dimensions can be parametrized using both Euler angles and unit quaternions. This article explains how to convert between the two representations. Actually this simple use of "quaternions" was first presented by Euler some seventy years earlier than Hamilton to solve the problem of magic squares. For this reason the dynamics community commonly refers to quaternions in this application as "Euler parameters".
Contents
Definition
A unit quaternion can be described as:
We can associate a quaternion with a rotation around an axis by the following expression
where α is a simple rotation angle (the value in radians of the angle of rotation) and cos(βx), cos(βy) and cos(βz) are the "direction cosines" locating the axis of rotation (Euler's Theorem).
Rotation matrices
The orthogonal matrix (post-multiplying a column vector) corresponding to a clockwise/left-handed rotation by the unit quaternion q = q0 + iq1 + jq2 + kq3 is given by the inhomogeneous expression
or equivalently, by the homogeneous expression
If q0 + iq1 + jq2 + kq3 is not a unit quaternion then the homogeneous form is still a scalar multiple of a rotation matrix, while the inhomogeneous form is in general no longer an orthogonal matrix. This is why in numerical work the homogeneous form is to be preferred if distortion is to be avoided.
The orthogonal matrix (post-multiplying a column vector) corresponding to a clockwise/left-handed rotation with Euler angles φ, θ, ψ, with x-y-z convention, is given by:
Conversion
By combining the quaternion representations of the Euler rotations we get
For Euler angles we get:
arctan and arcsin have a result between −π/2 and π/2. With three rotation between −π/2 and π/2 you can't have all possible orientations. You need to replace the arctan by atan2 to generate all the orientation.
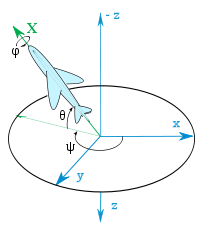
Relationship with Tait–Bryan angles
Similarly for Euler angles, we use the Tait–Bryan angles (in terms of flight dynamics):
- Roll – ϕ: rotation about the X-axis
- Pitch – θ: rotation about the Y-axis
- Yaw – ψ: rotation about the Z-axis
where the X-axis points forward, Y-axis to the right and Z-axis downward and in the example to follow the rotation occurs in the order yaw, pitch, roll (about body-fixed axes).
Singularities
One must be aware of singularities in the Euler angle parametrization when the pitch approaches ±90° (north/south pole). These cases must be handled specially. The common name for this situation is gimbal lock.
Code to handle the singularities is derived on this site: www.euclideanspace.com
See also
- Rotation operator (vector space)
- Quaternions and spatial rotation
- Euler Angles
- Rotation matrix
- Rotation representation (mathematics)
External links
- Q60. How do I convert Euler rotation angles to a quaternion? and related questions at The Matrix and Quaternions FAQ
Categories:- Rotation in three dimensions
- Euclidean symmetries
- 3D computer graphics
Wikimedia Foundation. 2010.











![\mathbf{q} = R_z(\psi)R_y(\theta)R_x(\phi) = [\cos (\psi /2) + \mathbf{k}\sin (\psi /2)][\cos (\theta /2) + \mathbf{j}\sin (\theta /2)][\cos (\phi /2) + \mathbf{i}\sin (\phi /2)]](9/bb904981a020685900d9320e9b41f09b.png)