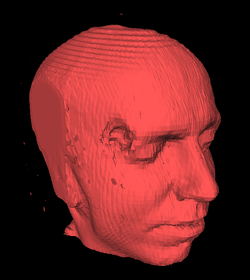
Marching cubes

Marching cubes
Head and cerebral structures (hidden) extracted from 150 MRI slices using marching-cubes (about 150,000 triangles)

Marching cubes is a computer graphics algorithm, published in the 1987 SIGGRAPH proceedings by Lorensen and Cline,[1] for extracting a polygonal mesh of an isosurface from a three-dimensional scalar field (sometimes called voxels). An analogous two-dimensional method is called the marching squares algorithm.

The algorithm proceeds through the scalar field, taking eight neighbor locations at a time (thus forming an imaginary cube), then determining the polygon(s) needed to represent the part of the isosurface that passes through this cube. The individual polygons are then fused into the desired surface.

This is done by creating an index to a precalculated array of 256 possible polygon configurations (28 = 256) within the cube, by treating each of the 8 scalar values as a bit in an 8-bit integer. If the scalar's value is higher than the iso-value (i.e., it is inside the surface) then the appropriate bit is set to one, while if it is lower (outside), it is set to zero. The final value after all 8 scalars are checked, is the actual index to the polygon indices array.

Finally each vertex of the generated polygons is placed on the appropriate position along the cube's edge by linearly interpolating the two scalar values that are connected by that edge.

The gradient of the scalar field at each grid point is also the normal vector of a hypothetical isosurface passing from that point. Therefore, we may interpolate these normals along the edges of each cube to find the normals of the generated vertices which are essential for shading the resulting mesh with some illumination model.

The applications of this algorithm are mainly concerned with medical visualizations such as CT and MRI scan data images, and special effects or 3-D modelling with what is usually called metaballs or other metasurfaces.

Contents

History

The Algorithm was developed by William E. Lorensen and Harvey E. Cline as a result of their research for General Electric. At General Electric they worked on a way to efficiently visualize data from CT and MRI devices.

The originally published 15 cube configurations

Their first published version exploited rotational and reflective symmetry and also sign changes to build the table with 15 unique cases. Unfortunately they made some mistakes. The minor one was that "case 14" - the 15th, because they started at "case 0" - was actually a symmetric image of case 11, but more importantly their base cases could lead to topological wrong decisions. For example case 11 should fit to a rotated and sign changed version of case 3, but it didn't. This led to non-watertight surfaces produced by their algorithm.

The problem was that for cases where you have "rippling" signs, you can have at least two correct choices for where the correct contour should pass. It actually doesn't matter which choice you take, but you have to make this choice topologically consistent. Their original cases made consistent choices, but the sign change could lead to mistakes. Thus, a corrected table includes their 14 unique cases, plus 14 correct sign changed cases, so 28 cases in total.

Later versions, such as Marching Cubes 33 by Evgeni V. Chernyaev[2] or the Asymptotic Decider [3] corrected these mistakes.

Patent issues

The Marching Cubes algorithm is claimed by anti-software patent advocates as a prime example in the graphics field of the woes of patenting software. An implementation was patented (United States Patent 4,710,876[4]) despite being a relatively obvious solution to the surface-generation problem, they claim. Another similar algorithm was developed, called Marching Tetrahedrons, in order to circumvent the patent as well as solve a minor ambiguity problem of marching cubes with some cube configurations. This patent expired in 2005, and it is now legal for the graphics community to use it without royalties since more than 17 years have passed from its issue date (December 1, 1987[5]).

Sources

  1. ^ William E. Lorensen, Harvey E. Cline: Marching Cubes: A high resolution 3D surface construction algorithm. In: Computer Graphics, Vol. 21, Nr. 4, July 1987
  2. ^ Chernyaev, Evgeni V. (1995). Marching Cubes 33: Construction of Topologically Correct Isosurfaces. 
  3. ^ Nielson, Gregory M. (1991). "The asymptotic decider: resolving the ambiguity in marching cubes". Proceeding VIS '91 Proceedings of the 2nd conference on Visualization '91. http://dl.acm.org/citation.cfm?id=949621. 
  4. ^ Marching Cubes, US Patent Office entry
  5. ^ Marching Cubes, US Patent Office entry

See also

External links


Wikimedia Foundation. 2010.

Игры ⚽ Поможем сделать НИР

Look at other dictionaries:

  • Marching Cubes — Tête et structures cérébrales (cachées) obtenues par l application des marching cubes sur 150 tranches provenant d un IRM (env. 150 000 triangles) Les « marching cubes » désignent un algorithme d infographie publié à la conférence… …   Wikipédia en Français

  • Marching Cubes — Polygonmodell eines Kopfes, der mittels Marching Cube aus 150 MRT Schichten extrahiert wurde ( 150.000 Dreiecke) Marching Cubes ist ein Algorithmus zur Berechnung von Isoflächen in der 3D Computergrafik. Er nähert eine Voxelgrafik durch eine… …   Deutsch Wikipedia

  • Marching cubes — Модель, построенная из 150 слоев с МРТ с использованием алгоритма marching cubes. Под поверхностью находятся около 150 000 полигонов и скрытых объектов. Размер сетки составляет 64 × 64 × 150 вокселей, кодированных 8 ю… …   Википедия

  • Marching cubes — Tête et structures cérébrales (cachées) obtenues par l application des marching cubes sur 150 tranches provenant d un IRM (env. 150 000 triangles) Les « marching cubes » désignent un algorithme d infographie publié à la conférence… …   Wikipédia en Français

  • Marching Tetrahedra — Introduction Cette méthode est destinée à représenter la surface définie par , avec f une fonction définie sur l espace. Le principe de base est identique au marching cubes. On notera alors que le marching cubes est une technique ayant fait… …   Wikipédia en Français

  • Marching Squares — Les Marching squares designent un algorithme de reconstruction de surface implicites (ou isosurfaces) en deux dimensions. Le principe est le même que pour les Marching cubes, mais fonctionnant sur un plan, utilisant donc des carrés au lieux de… …   Wikipédia en Français

  • Marching squares — is a computer graphics algorithm that generates contours for a two dimensional scalar field (rectangular array of individual numerical values). A similar method can be used to contour 2D triangle meshes. The contours can be of two kinds: Isolines …   Wikipedia

  • Marching Cube — Polygonmodell eines Kopfes, der mittels Marching Cube aus 150 MRT Schichten extrahiert wurde ( 150.000 Dreiecke) Marching Cubes ist ein Algorithmus zur Berechnung von Isoflächen in der 3D Computergrafik. Er nähert eine Voxelgrafik durch eine… …   Deutsch Wikipedia

  • Marching tetrahedrons — A cube divided into six tetrahedrons, with one tetrahedron shaded Marching tetrahedrons is an algorithm in the field of computer graphics to render implicit surfaces. It clarifies a minor ambiguity problem of marching cubes with some cube… …   Wikipedia

  • Marching tetrahedra — Cette méthode est destinée à représenter la surface définie par , avec f une fonction définie sur l espace. Le principe de base est identique au marching cubes. On notera alors que le marching cubes est une technique ayant fait l’objet d’un… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”