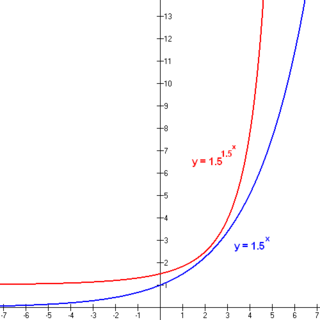
Double exponential function

A double exponential function (red curve) compared to a single exponential function (blue curve).

A double exponential function is a constant raised to the power of an exponential function. The general formula is $f(x) = a^{b^x}$, which grows much more quickly than an exponential function. For example, if a = b = 10:

• f(−1) ≈ 1.26
• f(0) = 10
• f(1) = 10¹⁰
• f(2) = 10¹⁰⁰ = googol
• f(3) = 10¹⁰⁰⁰
• f(100) = 10¹⁰¹⁰⁰ = googolplex.

Factorials grow faster than exponential functions, but much slower than double-exponential functions. The hyper-exponential function and Ackermann function grow even faster. See Big O notation for a comparison of the rate of growth of various functions.

The inverse of a double exponential function is a double logarithm.

Doubly exponential sequences

Aho and Sloane observed that in several important integer sequences, each term is a constant plus the square of the previous term, and show that such sequences can be formed by rounding to the nearest integer the values of a doubly exponential function in which the middle exponent is two.^[1] Integer sequences with this squaring behavior include

• The Fermat numbers

$F(m) = 2^{2^m}+1$

• The harmonic primes: The primes p, in which the sequence 1/2+1/3+1/5+1/7+....+1/p exceeds 0,1,2,3,....

The first few numbers, starting with 0, are 2,5,277,5195977,... (sequence A016088 in OEIS)

• The Double Mersenne numbers

$MM(p) = 2^{2^p-1}-1$

• The elements of Sylvester's sequence (sequence A000058 in OEIS)

$s_n = \left\lfloor E^{2^{n+1}}+\frac12 \right\rfloor$

where E ≈ 1.264084735305 is Vardi's constant.

• The number of k-ary operators:

$2^{2^n}$

More generally, if the nth value of an integer sequences is proportional to a double exponential function of n, Ionascu and Stanica call the sequence "almost doubly-exponential" and describe conditions under which it can be defined as the floor of a doubly-exponential sequence plus a constant.^[2] Additional sequences of this type include

• The prime numbers 2, 11, 1361, ... (sequence A051254 in OEIS)

$a(n) = \left\lfloor A^{3^n}\right\rfloor$

where A ≈ 1.306377883863 is Mills' constant.

Applications

Algorithmic complexity

In computational complexity theory, some algorithms take double-exponential time:

• Decision procedures for Presburger arithmetic
• Computing a Gröbner basis
• Finding a complete set of associative-commutative unifiers ^[3]
• Satisfying CTL⁺ (which is, in fact, 2-EXPTIME-complete) ^[4]
• Quantifier elimination on real closed fields takes at least doubly-exponential time (but is not even known to be computable in ELEMENTARY)
• Calculating the complement of a regular expression

Number theory

Some number theoretical bounds are double exponential. Odd perfect numbers with n distinct prime factors are known to be at most

$2^{4^n}$

a result of Nielsen (2003).^[5]

The largest known prime number in the electronic era has grown roughly as a double exponential function of the year since Miller and Wheeler found a 79-digit prime on EDSAC1 in 1951.^[6]

Theoretical biology

In population dynamics the growth of human population is sometimes supposed to be double exponential. Gurevich and Varfolomeyev^[7] experimentally fit

$N(y)=375.6\cdot 1.00185^{1.00737^{y-1000}} \,$

where N(y) is the population in year y in millions.

Physics

In the Toda oscillator model of self-pulsation, the logarithm of amplitude varies exponentially with time (for large amplitudes), thus the amplitude varies as double-exponential function of time.^[8]

References

1. ^ Aho, A. V.; Sloane, N. J. A. (1973), "Some doubly exponential sequences", Fibonacci Quarterly 11: 429–437, http://www.research.att.com/~njas/doc/doubly.html .
2. ^ Ionascu, E.; Stanica, P. (2004), "Effective asymptotics for some nonlinear recurrences and almost doubly-exponential sequences", Acta Mathematica Universitatis Comenianae LXXIII (1): 75–87 .
3. ^ Kapur, Deepak; Narendran, Paliath (1992), "Double-exponential complexity of computing a complete set of AC-unifiers", Proc. 7th IEEE Symp. Logic in Computer Science (LICS 1992), pp. 11–21, doi:10.1109/LICS.1992.185515, ISBN 0-8186-2735-2, http://citeseer.ist.psu.edu/337363.html .
4. ^ Johannse, Jan; Lange, Martin (2003), "CTL⁺ is complete for double exponential time", in Baeten, Jos C. M.; Lenstra, Jan Karel; Parrow, Joachim et al., Proc. 30th Int. Colloq. Automata, Languages, and Programming (ICALP 2003), Lecture Notes in Computer Science, 2719, Springer-Verlag, pp. 767–775, doi:10.1007/3-540-45061-0_60, ISBN 978-3-540-40493-4, http://www.tcs.informatik.uni-muenchen.de/~mlange/papers/icalp03.pdf .
5. ^ Nielsen, Pace P. (2003), "An upper bound for odd perfect numbers", INTEGERS: the Electronic Journal of Combinatorial Number Theory 3: A14, http://www.integers-ejcnt.org/vol3.html .
6. ^ Miller, J. C. P.; Wheeler, D. J. (1951), "Large prime numbers", Nature 168 (4280): 838, Bibcode 1951Natur.168..838M, doi:10.1038/168838b0 .
7. ^ Varfolomeyev, S. D.; Gurevich, K. G. (2001), "The hyperexponential growth of the human population on a macrohistorical scale", Journal of Theoretical Biology 212 (3): 367–372, doi:10.1006/jtbi.2001.2384, PMID 11829357 .
8. ^ Kouznetsov, D.; Bisson, J.-F.; Li, J.; Ueda, K. (2007), "Self-pulsing laser as oscillator Toda: Approximation through elementary functions", Journal of Physics A 40 (9): 1–18, Bibcode 2007JPhA...40.2107K, doi:10.1088/1751-8113/40/9/016, http://www.iop.org/EJ/abstract/-search=15823442.1/1751-8121/40/9/016 .