Cyclonic separation

A simple cyclone separator

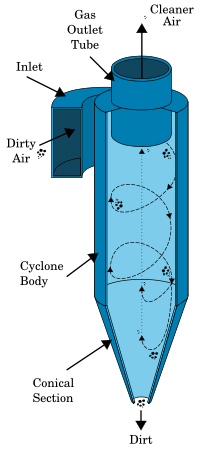
Cyclonic separation is a method of removing particulates from an air, gas or liquid stream, without the use of filters, through vortex separation. Rotational effects and gravity are used to separate mixtures of solids and fluids. The method can also be used to separate fine droplets of liquid from a gaseous stream.

A high speed rotating (air)flow is established within a cylindrical or conical container called a cyclone. Air flows in a helical pattern, beginning at the top (wide end) of the cyclone and ending at the bottom (narrow) end before exiting the cyclone in a straight stream through the center of the cyclone and out the top. Larger (denser) particles in the rotating stream have too much inertia to follow the tight curve of the stream, and strike the outside wall, then falling to the bottom of the cyclone where they can be removed. In a conical system, as the rotating flow moves towards the narrow end of the cyclone, the rotational radius of the stream is reduced, thus separating smaller and smaller particles. The cyclone geometry, together with flow rate, defines the cut point of the cyclone. This is the size of particle that will be removed from the stream with a 50% efficiency. Particles larger than the cut point will be removed with a greater efficiency, and smaller particles with a lower efficiency.

Airflow diagram for Aerodyne cyclone in standard vertical position. Secondary air flow is injected to reduce wall abrasion.

Airflow diagram for Aerodyne cyclone in horizontal position, an alternate design. Secondary air flow is injected to reduce wall abrasion, and to help move collected particulates to hopper for extraction.

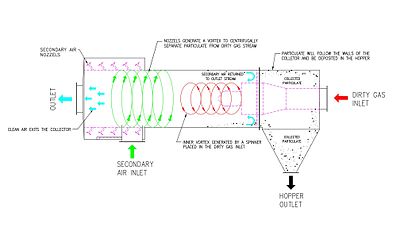
An alternative cyclone design uses a secondary air flow within the cyclone to keep the collected particles from striking the walls, to protect them from abrasion. The primary air flow containing the particulates enters from the bottom of the cyclone and is forced into spiral rotation by stationary spinner vanes. The secondary air flow enters from the top of the cyclone and moves downward toward the bottom, intercepting the particulate from the primary air. The secondary air flow also allows the collector to optionally be mounted horizontally, because it pushes the particulate toward the collection area, and does not rely solely on gravity to perform this function.

Large scale cyclones are used in sawmills to remove sawdust from extracted air. Cyclones are also used in oil refineries to separate oils and gases, and in the cement industry as components of kiln preheaters. Cyclones are increasingly used in the household, as the core technology in bagless types of portable vacuum cleaners and central vacuum cleaners. Cyclones are also used in industrial and professional kitchens for separating the grease from the exhaust air in extract hoods.^[1] Smaller cyclones are used to separate airborne particles for analysis. Some are small enough to be worn clipped to clothing, and are used to separate respirable particles for later analysis.

Analogous devices for separating particles or solids from liquids are called hydrocyclones or hydroclones. These may be used to separate solid waste from water in wastewater and sewage treatment.

Cyclone theory

Steady state

As the cyclone is essentially a two phase particle-fluid system, fluid mechanics and particle transport equations can be used to describe the behaviour of a cyclone. The air in a cyclone is initially introduced tangentially into the cyclone with an inlet velocity V_in. Assuming that the particle is spherical, a simple analysis to calculate critical separation particle sizes can be established.

Given that the fluid velocity is moving in a spiral the gas velocity can be broken into two component velocities: a tangential component, V_t, and a radial velocity component V_r. Assuming Stokes' law, the drag force on any particle in this inlet stream is therefore given by the following equation:

F_d = 6πr_pμV_r.

If one considers an isolated particle circling in the upper cylindrical component of the cyclone at a rotational radius of r from the cyclone's central axis, the particle is therefore subjected to centrifugal, drag and buoyant forces. The centrifugal component is given by:

$F_c= m \frac{V_t^2}{r}$

$= \frac{4}{3} \pi \rho_p r_p^3 \frac{V_t^2 }{r} .$

The buoyant force component is obtained by the difference between the particle and fluid densities, ρ_p and ρ_f respectively:

$F_b = -V_p\rho_f \frac{V_t^2}{r}$

$= -\frac{4 \pi r_p^3}{3} \frac{V_t^2}{r}\rho_f .$

The force balance can be created by summing the forces together

$\frac{dr}{dt} = F_d + F_c + F_b$

This rate is controlled by the diameter of the particle's orbit around the central axis of the cyclone. A particle in the cyclonic flow will move towards either the wall of the cyclone, or the central axis of the cyclone until the drag, buoyant and centrifugal forces are balanced. Assuming that the system has reached steady state, the particles will assume a characteristic radius dependent upon the force balance. Heavier, denser particles will assume a solid flow at some larger radius than light particles. The steady state balance assumes that for all particles, the forces are equated, hence:

F_d + F_c + F_b = 0

Which expands to:

$6\pi r_p \mu V_r+ \frac{4}{3}\pi r_p^3 \frac{V_t^2}{r}\rho_p - \frac{4}{3}\pi r_p^3 \frac{V_t^2}{r}\rho_f =0$

This can be expressed by rearranging the above in terms of the particle radius. The particle radius as a function of cyclonic radius, fluid density and fluid tangential and rotational velocities can then be found to be:

$r_p = 3 \left( \frac{\mu V_r r}{2 V_t^2 (\rho_p -\rho_f)} \right)^{\frac{1}{2}} .$

Experimentally it is found that the velocity component of rotational flow is proportional to r²,^[2] therefore:

$V_t \propto r^2 .$

This means that the established feed velocity controls the vortex rate inside the cyclone, and the velocity at an arbitrary radius is therefore:

$U_r = U_{in}\frac{r}{R_{in}} .$

Subsequently, given a value for V_t, possibly based upon the injection angle, and a cutoff radius, a characteristic particle filtering radius can be estimated, above which particles will be removed from the gas stream.

Alternative Steady State Analysis

Assume we have a particle of radius r_p and density ρ_p moving with a parcel of fluid of viscosity μ_f and density ρ_f. The particle and the fluid are moving along a curved trajectory with tangential velocity V_t with a radius of curvature of r_c.

If we view the particle in a frame of reference moving with the fluid, we can describe the behavior of the particle by invoking the imaginary, inertial centrifugal force acting as a form of gravity directed outward, away from the axis of rotation. The magnitude of the centrifugal force will be given by

$F_c = m_p \frac{V_t^2}{r_c}$.

where m_p is the mass of the particle.

If we ignore the universal downward force of gravity and viscous drag between the particle and the fluid parallel to the velocity, there are two other forces acting on the particle - radial viscous drag and buoyancy.

The viscous drag (F_d ) between the particle and the fluid resulting from radial movement of the particle through the fluid is given by

F_d = − 6πr_pμ_fV_r

where V_r is the radial drift velocity of the particle through the fluid and the sign reflects the opposition of the force to the motion.

The buoyancy force (F_b) exerted on the particle by the fluid is given by

$F_b = \rho _f v_p \frac{V_t^2}{r_c}$

where v_p is the volume of the particle

If we assign upward (toward the center of rotation) as the positive radial direction (+) in our frame of reference, then F_c will be pointed in the negative direction, F_b will be pointed in the positive direction and the direction of F_d will depend on the direction of v_p.

If we assume the system has reached dynamic equilibrium then the sum of the forces is zero

F_b + F_d + F_c = 0.

After applying the appropriate signs and expanding m_p and v_p explicitly we have

$\frac{4}{3} \pi r_p^3 \rho _f \frac{V_t^2}{r_c} - 6 \pi r_p \mu_f V_{r} - \frac{4}{3} \pi r_p^3 \rho _p \frac{V_t^2}{r_c} = 0$

Solving this equation for V_r we have

$V_r = \frac{2}{9} \frac{r_p^2}{\mu _f} \frac{V_t^2}{r_c} (\rho _f - \rho _p)$.

Notice that if the density of the fluid is greater than the density of the particle, the motion is (+), toward the center of rotation and if the particle is denser than the fluid, the motion is (-), away from the center.

Expressing the motion in terms of angular velocity ω we have

$V_t^2 = \omega ^2 r_c^2$

Substituting into the equation above yields

$V_r = \frac{2}{9} \frac{r_p^2}{\mu _f} \omega ^2 r_c (\rho _f - \rho _p)$.

In this analysis, V_r is the drift velocity at which dynamic equilibrium is attained - the drag friction generated by the movement of the particle through the fluid balances the centrifugal force of the rotation and the particle has no radial acceleration, traveling at a constant velocity. In the extreme case where μ_f = 0 (a fluid with no viscosity) the equilibrium drift velocity is undefined – the particle can accelerate without ever reaching equilibrium. In the opposite extreme, μ_f = ∞, the equilibrium drift velocity is 0, there is no outward radial movement and the particle is frozen in the fluid

In non-equilibrium conditions, the general case equation F=ma must be solved

$a_r = -\frac{9}{2} \frac{\mu_f}{\rho_p r_p^2}v_r + \left( \frac{\rho_f}{\rho_p}-1 \right) \omega^2 r_c$

The presence of both a_r and v_r makes this a differential equation and complicates the solution. Note that if the densities of the particle and fluid are equal, the solution is a_r = v_r = 0 and cyclonic separation is not possible.

In a cyclone particle separator, the design objective is to control the system geometry and the operating parameters so that the drift velocity will move the particle out of the carrier fluid, before the fluid exits via the outlet tube. In most cases, the steady state solution is used as guidance in designing a separator, but the actual performance must be evaluated and modified empirically.

Alternate models

The above equations are relatively simple and provide a basic approximation to the behaviour of a cyclone separator. These equations are, however, limited in many regards. For example, the geometry of the separator is not considered, the particles are assumed to achieve a steady state and the effect of the vortex inversion at the base of the cyclone is also ignored, all behaviours which are unlikely to be achieved in a cyclone at real operating conditions.

More complex differential equation based models exist, as many authors have studied the behaviour of cyclone separators.^[3] Numerical modelling using computational fluid dynamics has also been used extensively in the study of cyclonic behaviour.^[4][5]

See also

Physics portal

• Air filter
• Centrifuge
• Dust collector
• Helikon vortex separation process
• Spiral separator
• Trickle valve

References

• High Efficiency Horizontal Dust Collection

1. ^ Jeven Oy. "How cyclone grease separators work". http://www.jeven.com/mvhome/homepage_item_view.html?id=00001285&did=298&lang=en&page_category_id=75354. 
2. ^ Rhodes M. (1998). Introduction to particle technology. John Wiley and Sons. ISBN 0471984833. 
3. ^ Smith, J. L, Jr.. PhD thesis: Experimental and Analytical Study of the Vortex in the Cyclone Separator. http://dspace.mit.edu/handle/1721.1/11792. 
4. ^ Martignoni, W. P.; Bernardo, S.; Quintani, C. L. (2007). "Evaluation of cyclone geometry and its influence on performance parameters by computational fluid dynamics (CFD)". Brazilian Journal of Chemical Engineering 24. doi:10.1590/S0104-66322007000100008. http://www.scielo.br/scielo.php?pid=S0104-66322007000100008&script=sci_arttext. 
5. ^ PhD Thesis: On the Potential of Large Eddy Simulation to Simulate Cyclone Separators. http://archiv.tu-chemnitz.de/pub/2007/0013/data/diss.pdf.